Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-13T10:20:45.381Z Has data issue: false hasContentIssue false
  • English
  • Français

Products of twists, geodesic lengths and Thurston shears

Part of: Symplectic geometry, contact geometry Riemann surfaces Deformations of analytic structures Other groups of matrices

Published online by Cambridge University Press:  09 October 2014

Scott A. Wolpert
Scott A. Wolpert*
Affiliation:
University of Maryland, College Park, MD 20742-4015, USA email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Thurston introduced shear deformations (cataclysms) on geodesic laminations–deformations including left and right displacements along geodesics. For hyperbolic surfaces with cusps, we consider shear deformations on disjoint unions of ideal geodesics. The length of a balanced weighted sum of ideal geodesics is defined and the Weil–Petersson (WP) duality of shears and the defined length is established. The Poisson bracket of a pair of balanced weight systems on a set of disjoint ideal geodesics is given in terms of an elementary 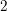$2$-form. The symplectic geometry of balanced weight systems on ideal geodesics is developed. Equality of the Fock shear coordinate algebra and the WP Poisson algebra is established. The formula for the WP Riemannian pairing of shears is also presented.

Keywords

Teichmüller spaceWeil–Petersson geometrygeodesic-length functionsshear and twist deformationsFock shear coordinate algebra

MSC classification

Primary: 30F60: Teichmüller theory
Secondary: 20H10: Fuchsian groups and their generalizations 32G15: Moduli of Riemann surfaces, Teichmüller theory 53D30: Symplectic structures of moduli spaces
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 2 , February 2015 , pp. 313 - 350
Copyright
© The Author 2014 

References

Abikoff, W., Degenerating families of Riemann surfaces, Ann. of Math. (2) 105 (1977), 29–44.Google Scholar
Abikoff, W., The real analytic theory of Teichmüller space (Springer, Berlin, 1980).Google Scholar
Ahlfors, L. V., Some remarks on Teichmüller’s space of Riemann surfaces, Ann. of Math. (2) 74 (1961), 171–191.Google Scholar
Ahlfors, L. V., Lectures on quasiconformal mappings, University Lecture Series, vol. 38, second edition (American Mathematical Society, Providence, RI, 2006), with supplemental chapters by C. J. Earle, I. Kra, M. Shishikura and J. H. Hubbard.Google Scholar
Ahlfors, L. and Bers, L., Riemann’s mapping theorem for variable metrics, Ann. of Math. (2) 72 (1960), 385–404.Google Scholar
Bers, L., Spaces of degenerating Riemann surfaces, in Discontinuous groups and Riemann surfaces (Proc. Conf., Univ. Maryland, College Park, Md., 1973), Annals of Mathematics Studies, no. 79. (Princeton University Press, Princeton, NJ, 1974), 43–55.Google Scholar
Bonahon, F., Shearing hyperbolic surfaces, bending pleated surfaces and Thurston’s symplectic form, Ann. Fac. Sci. Toulouse Math. (6) 5 (1996), 233–297.Google Scholar
Bonahon, F., Geodesic laminations with transverse Hölder distributions, Ann. Sci. Éc. Norm. Supér. (4) 30 (1997), 205–240.Google Scholar
Bonahon, F., Transverse Hölder distributions for geodesic laminations, Topology 36 (1997), 103–122.Google Scholar
Buser, P., Geometry and spectra of compact Riemann surfaces, Progress in Mathematics, vol. 106 (Birkhäuser, Boston, MA, 1992).Google Scholar
Chabauty, C., Limite d’ensembles et géométrie des nombres, Bull. Soc. Math. France 78 (1950), 143–151.Google Scholar
Fok, V. V. and Chekhov, L. O., Quantum Teichmüller spaces, Teoret. Mat. Fiz. 120 (1999), 511–528.Google Scholar
Fock, V. and Goncharov, A., Moduli spaces of local systems and higher Teichmüller theory, Publ. Math. Inst. Hautes Études Sci. 103 (2006), 1–211.CrossRefGoogle Scholar
Fock, V. V. and Goncharov, A. B., Dual Teichmüller and lamination spaces, in Handbook of Teichmüller theory, Vol. I, IRMA Lectures in Mathematics and Theoretical Physics, vol. 11 (European Mathematical Society, Zürich, 2007), 647–684.CrossRefGoogle Scholar
Gardiner, F. P., Schiffer’s interior variation and quasiconformal mapping, Duke Math. J. 42 (1975), 371–380.CrossRefGoogle Scholar
Harvey, W., Chabauty spaces of discrete groups, in Discontinuous groups and Riemann surfaces (Proc. Conf., Univ. Maryland, College Park, Md., 1973), Annals of Mathematics Studies, vol. 79 (Princeton University Press, Princeton, NJ, 1974), 239–246.Google Scholar
Harvey, W. J. (ed.), Discrete groups and automorphic functions (Academic Press [Harcourt Brace Jovanovich Publishers], London, 1977).Google Scholar
Hejhal, D. A., Monodromy groups and Poincaré series, Bull. Amer. Math. Soc. 84 (1978), 339–376.Google Scholar
Hubbard, J. H., Teichmüller theory and applications to geometry, topology, and dynamics, Vol. 1 (Matrix Editions, Ithaca, NY, 2006), Teichmüller theory, with contributions by A. Douady, W. Dunbar, R. Roeder, S. Bonnot, D. Brown, A. Hatcher, C. Hruska and S. Mitra, With forewords by W. Thurston and C. Earle.Google Scholar
Imayoshi, Y. and Taniguchi, M., An introduction to Teichmüller spaces (Springer, Tokyo, 1992) (translated and revised from the Japanese by the authors).Google Scholar
Kahn, J. and Markovic, V., Random ideal triangulations and the Weil–Petersson distance between finite degree covers of punctured Riemann surfaces, Preprint (2008), arXiv:math/0806.2304.Google Scholar
Papadopoulos, A. and Penner, R. C., The Weil–Petersson symplectic structure at Thurston’s boundary, Trans. Amer. Math. Soc. 335 (1993), 891–904.Google Scholar
Penner, R. C., The decorated Teichmüller space of punctured surfaces, Comm. Math. Phys. 113 (1987), 299–339.Google Scholar
Penner, R. C., Weil–Petersson volumes, J. Differential Geom. 35 (1992), 559–608.Google Scholar
Penner, R. C., Cell decomposition and compactification of Riemann’s moduli space in decorated Teichmüller theory, in Woods Hole Mathematics, Series on Knots and Everything, vol. 34 (World Scientific, Hackensack, NJ, 2004), 263–301.Google Scholar
Penner, R. C., Decorated Teichmüller theory, The QGM Master Class Series (European Mathematical Society, Zürich, 2012).Google Scholar
Penner, R. C. and Harer, J. L., Combinatorics of train tracks (Princeton University Press, Princeton, NJ, 1992).CrossRefGoogle Scholar
Riera, G., A formula for the Weil–Petersson product of quadratic differentials, J. Anal. Math. 95 (2005), 105–120.Google Scholar
Sözen, Y. and Bonahon, F., The Weil–Petersson and Thurston symplectic forms, Duke Math. J. 108 (2001), 581–597.Google Scholar
Thurston, W. P., Minimal stretch maps between hyperbolic surfaces, Preprint (1998),arXiv:math/9801039.Google Scholar
Wolpert, S. A., The Fenchel–Nielsen deformation, Ann. of Math. (2) 115 (1982), 501–528.Google Scholar
Wolpert, S. A., On the symplectic geometry of deformations of a hyperbolic surface, Ann. of Math. (2) 117 (1983), 207–234.Google Scholar
Wolpert, S. A., The hyperbolic metric and the geometry of the universal curve, J. Differential Geom. 31 (1990), 417–472.Google Scholar
Wolpert, S. A., Cusps and the family hyperbolic metric, Duke Math. J. 138 (2007), 423–443.Google Scholar
Wolpert, S. A., Extension of the Weil–Petersson connection, Duke Math. J. 146 (2009), 281–303.Google Scholar
Wolpert, S. A., Families of Riemann surfaces and Weil–Petersson geometry, CBMS Regional Conference Series in Mathematics, vol. 113 (Conference Board of the Mathematical Sciences, Washington, DC, 2010).Google Scholar
Wolpert, S. A., Geodesic-length functions and the Weil–Petersson curvature tensor, J. Differential Geom. 91 (2012), 321–359.Google Scholar