Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-13T10:19:42.187Z Has data issue: false hasContentIssue false
  • English
  • Français

Unnormalized differences between zeros of L-functions

Part of: Probabilistic theory: distribution modulo $1$; metric theory of algorithms Zeta and $L$-functions: analytic theory

Published online by Cambridge University Press:  24 October 2014

Kevin Ford  and
Alexandru Zaharescu
Kevin Ford
Affiliation:
Department of Mathematics, 1409 West Green Street, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA email [email protected]
Alexandru Zaharescu
Affiliation:
Department of Mathematics, 1409 West Green Street, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study a subtle inequity in the distribution of unnormalized differences between imaginary parts of zeros of the Riemann zeta function, which was observed by a number of authors. We establish a precise measure which explains the phenomenon, that the location of each Riemann zero is encoded in the distribution of large Riemann zeros. We also extend these results to zeros of more general 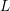$L$-functions. In particular, we show how the rank of an elliptic curve over 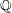$\mathbb{Q}$ is encoded in the sequences of zeros of other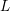$L$-functions, not only the one associated to the curve.

Keywords

Riemann zeta functionL-functionsdistribution of zeros

MSC classification

Primary: 11M26: Nonreal zeros of $zeta (s)$ and $L(s, chi)$; Riemann and other hypotheses
Secondary: 11K38: Irregularities of distribution, discrepancy
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 2 , February 2015 , pp. 230 - 252
Copyright
© The Author(s) 2014 

References

Berry, M. V. and Keating, J. P., The Riemann zeros and eigenvalue asymptotics, SIAM Rev. 41 (1999), 236–266.Google Scholar
Birch, B. J. and Swinnerton-Dyer, H. P. F., Notes on elliptic curves. II, J. Reine Angew. Math. 218 (1965), 79–108.Google Scholar
Bogomolny, E. B. and Keating, J. P., Gutzwiller’s trace formula and spectral statistics: beyond the diagonal approximation, Phys. Rev. Lett. 77 (1996), 1472–1475.CrossRefGoogle ScholarPubMed
Breuil, C., Conrad, B., Diamond, F. and Taylor, R., On the modularity of elliptic curves over ℚ: wild 3-adic exercises, J. Amer. Math. Soc. 14 (2001), 843–939.Google Scholar
Conrey, J. B., Farmer, D. W. and Zirnbauer, M. R., Autocorrelation of ratios of L-functions, Commun. Number Theory Phys. 2 (2008), 593–636.CrossRefGoogle Scholar
Conrey, J. B. and Snaith, N. C., Applications of the L-functions ratios conjectures, Proc. Lond. Math. Soc. (3) 94 (2007), 594–646.CrossRefGoogle Scholar
Davenport, H., Multiplicative number theory, third edition (Springer, New York, 2000).Google Scholar
Duke, W., Friedlander, J. B. and Iwaniec, H., Bounds for automorphic L-functions, Invent. Math. 112 (1993), 1–8.Google Scholar
Dyson, F. J., Statistical theory of the energy levels of complex systems, I, II, III, J. Math. Phys. 3 (1962), 140–156, 157–165, 166–175.Google Scholar
Ford, K. and Zaharescu, A., On the distribution of imaginary parts of zeros of the Riemann zeta function, J. Reine Angew. Math. 579 (2005), 145–158.Google Scholar
Ford, K., Soundararajan, K. and Zaharescu, A., On the distribution of imaginary parts of zeros of the Riemann zeta function, II, Math. Ann. 343 (2009), 487–505.Google Scholar
Hafner, J. L., Explicit estimates in the arithmetic theory of cusp forms and Poincaré series, Math. Ann. 264 (1983), 9–20.Google Scholar
Heath-Brown, D. R., A new form of the circle method, and its application to quadratic forms, J. Reine Angew. Math. 481 (1996), 149–206.Google Scholar
Hejhal, D., On the triple correlation of the zeros of the zeta function, Int. Math. Res. Not. IMRN 1994 (1994), 293–302.Google Scholar
Iwaniec, H. and Kowalski, E., Analtytic number theory, Colloquium Publications, vol. 53 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Jacquet, H. and Shalika, J. A., On Euler products and the classification of automorphic representations. I., Amer. J. Math. 103 (1981), 499–558.Google Scholar
Jacquet, H. and Shalika, J. A., On Euler products and the classification of automorphic forms. II, Amer. J. Math. 103 (1981), 777–815.CrossRefGoogle Scholar
Kaczorowski, J., Analytic number theory, Lecture Notes in Mathematics, vol. 1891 (Springer, Berlin, 2006), 133–209.Google Scholar
Kaczorowski, J. and Perelli, A., The Selberg class: a survey, Number Theory in Progress, vol. II, eds Perelli, A. and Viola, C. (de Gruyter, Berlin, 1999), 953–992.Google Scholar
Katz, N. and Sarnak, P., Zeros of zeta functions and symmetry, Bull. Amer. Math. Soc. (N.S.) 36 (1999), 1–26.Google Scholar
Katz, N. and Sarnak, P., Random matrices, Frobenius eigenvalues, and monodromy, Colloquium Publications, vol. 45 (American Mathematical Society, Providence, RI, 1999).Google Scholar
Kowalski, E., Michel, P. and VanderKam, J., Rankin-Selberg L-functions in the level aspect, Duke Math. J. 114 (2002), 123–191.Google Scholar
Luo, W., Zeros of Hecke L-functions associated with cusp forms, Acta Arith. 71 (1995), 139–158.Google Scholar
Mœglin, C. and Waldspurger, J.-L., Le spectre résiduel de GL(n), Ann. Sci. Éc. Norm. Supér. 22 (1989), 605–674.Google Scholar
Montgomery, H. L., The pair correlation of zeros of the zeta function, in Analytic number theory, Proceedings of Symposia in Pure Mathematics, vol. XXIV, ed. Diamond, H. G. (American Mathematical Society, Providence, RI, 1972), 181–193.Google Scholar
Odlyzko, A. M., On the distribution of spacings between zeros of the zeta function, Math. Comp. 48 (1987), 273–308.CrossRefGoogle Scholar
Perelli, A., A survey of the Selberg class of L-functions, Part I, Milan J. Math. 73 (2005), 19–52.Google Scholar
Perelli, A., A Survey of the Selberg Class of L-functions. Part II, Riv. Mat. Univ. Parma 73 (2004), 83–118.Google Scholar
Pérez-Marco, R., Statistics on Riemann zeros, Preprint (2011), arXiv:1112.0346.Google Scholar
Rodgers, B., Macroscopic pair correlation of the Riemann zeroes for smooth test functions, Q. J. Math. 64 (2013), 1197–1219.Google Scholar
Rudnick, Z. and Sarnak, P., Zeros of principal L-functions and random matrix theory, Duke Math. J. 81 (1996), 269–322; A celebration of John F. Nash, Jr.Google Scholar
Selberg, A., Contributions to the theory of the Riemann zeta-function, Arch. Math. Naturvid. 48 (1946), 89–155; Collected papers, vol. I (Springer, Berlin, 1989), 214–280.Google Scholar
Selberg, A., Contributions to the theory of Dirichlet’s L-functions, Skr. Norske Vid. Akad. Oslo. I. 1946 (1946), 62; Collected papers, vol. I (Springer, Berlin, 1989), 281–340.Google Scholar
Selberg, A., Old and new conjectures and results about a class of Dirichlet series, in Proceedings of the Amalfi Conference on Analytic Number Theory, Maiori, 1989, University of Salerno (1992), 367–385; Collected papers, vol. II (Springer, Berlin, 1989), 47–63.Google Scholar
Shahidi, F., On nonvanishing of L-functions, Bull. Amer. Math. Soc. (N.S.) 2 (1980), 462–464.Google Scholar
Shahidi, F., On certain L-functions, Amer. J. Math. 103 (1981), 297–355.Google Scholar
Snaith, N. C., Riemann zeros and random matrix theory, Milan Math. J. 78 (2010), 135–152.Google Scholar
Taylor, R. and Wiles, A., Ring-theoretic properties of certain Hecke algebras, Ann. of Math. (2) 141 (1995), 553–572.Google Scholar
Wigner, E., Random matrices in physics, SIAM Rev. 9 (1967), 1–23.Google Scholar
Wiles, A., Modular elliptic curves and Fermat’s last theorem, Ann. of Math. (2) 142 (1995), 443–551.Google Scholar
Wiles, A., The Birch and Swinnerton-Dyer conjecture, in The millennium prize problems (Clay Mathematics Institute, Cambridge, MA, 2006), 31–41.Google Scholar