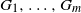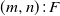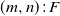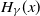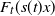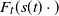Original Article
On the joint survival probability of two collaborating firms
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2023, pp. 369-384
-
- Article
-
- You have access
- HTML
- Export citation
Phase transition for the generalized two-community stochastic block model
- Part of:
-
- Published online by Cambridge University Press:
- 31 July 2023, pp. 385-400
-
- Article
-
- You have access
- HTML
- Export citation
Normal and stable approximation to subgraph counts in superpositions of Bernoulli random graphs
- Part of:
-
- Published online by Cambridge University Press:
- 18 August 2023, pp. 401-419
-
- Article
-
- You have access
- HTML
- Export citation
Duality theory for exponential utility-based hedging in the Almgren–Chriss model
- Part of:
-
- Published online by Cambridge University Press:
- 03 August 2023, pp. 420-438
-
- Article
-
- You have access
- HTML
- Export citation
Reliability analyses of linear two-dimensional consecutive k-type systems
- Part of:
-
- Published online by Cambridge University Press:
- 14 August 2023, pp. 439-464
-
- Article
-
- You have access
- HTML
- Export citation
Stochastic differential equation approximations of generative adversarial network training and its long-run behavior
- Part of:
-
- Published online by Cambridge University Press:
- 02 October 2023, pp. 465-489
-
- Article
-
- You have access
- HTML
- Export citation
Heavy-traffic limits for parallel single-server queues with randomly split Hawkes arrival processes
- Part of:
-
- Published online by Cambridge University Press:
- 07 August 2023, pp. 490-514
-
- Article
-
- You have access
- HTML
- Export citation
Stopping problems with an unknown state
- Part of:
-
- Published online by Cambridge University Press:
- 09 August 2023, pp. 515-528
-
- Article
-
- You have access
- HTML
- Export citation
Strong convergence of peaks over a threshold
- Part of:
-
- Published online by Cambridge University Press:
- 23 August 2023, pp. 529-539
-
- Article
-
- You have access
- HTML
- Export citation
Comparison theorem and stability under perturbation of transition rate matrices for regime-switching processes
- Part of:
-
- Published online by Cambridge University Press:
- 14 September 2023, pp. 540-557
-
- Article
-
- You have access
- HTML
- Export citation
R-positivity and the existence of zero-temperature limits of Gibbs measures on nearest-neighbor matrices
- Part of:
-
- Published online by Cambridge University Press:
- 25 September 2023, pp. 558-577
-
- Article
-
- You have access
- HTML
- Export citation
Optimal stopping methodology for the secretary problem with random queries
- Part of:
-
- Published online by Cambridge University Press:
- 02 October 2023, pp. 578-602
-
- Article
-
- You have access
- HTML
- Export citation
Stochastic ordering results on the duration of the gambler’s ruin game
- Part of:
-
- Published online by Cambridge University Press:
- 06 October 2023, pp. 603-621
-
- Article
-
- You have access
- HTML
- Export citation
Weak convergence of the extremes of branching Lévy processes with regularly varying tails
- Part of:
-
- Published online by Cambridge University Press:
- 06 December 2023, pp. 622-643
-
- Article
-
- You have access
- HTML
- Export citation
Resolving an old problem on the preservation of the IFR property under the formation of
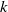 $k$-out-of-
$k$-out-of- $n$ systems with discrete distributions
$n$ systems with discrete distributions
- Part of:
-
- Published online by Cambridge University Press:
- 16 October 2023, pp. 644-653
-
- Article
-
- You have access
- HTML
- Export citation
Central limit theorem in complete feedback games
- Part of:
-
- Published online by Cambridge University Press:
- 16 October 2023, pp. 654-666
-
- Article
-
- You have access
- HTML
- Export citation
SIR model with social gatherings
- Part of:
-
- Published online by Cambridge University Press:
- 15 January 2024, pp. 667-684
-
- Article
-
- You have access
- HTML
- Export citation
The unified extropy and its versions in classical and Dempster–Shafer theories
- Part of:
-
- Published online by Cambridge University Press:
- 23 October 2023, pp. 685-696
-
- Article
-
- You have access
- HTML
- Export citation
Tessellation-valued processes that are generated by cell division
- Part of:
-
- Published online by Cambridge University Press:
- 01 November 2023, pp. 697-715
-
- Article
-
- You have access
- HTML
- Export citation
On a time-changed variant of the generalized counting process
- Part of:
-
- Published online by Cambridge University Press:
- 27 October 2023, pp. 716-738
-
- Article
-
- You have access
- HTML
- Export citation