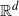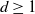1. Introduction
The study of random tessellations (or mosaics) is a substantial part of stochastic geometry. The Voronoi tessellations and Poisson hyperplane tessellations are classical and well-established. Motivated by modeling fracture or crack patterns as they are observed, for example, in geology, materials science, nanotechnology, or drying soil patterns [Reference Boulogne, Giorgiutti-Dauphiné and Pauchard2, Reference Hafver5, Reference Nandakishore and Goehring23, Reference Seghir and Arscott30, Reference Xia and Hutchinson31]; also, space–time processes of tessellations are considered where the cells are consecutively divided. Recently, such models are also of growing interest in the context of machine learning, see [Reference O’Reilly and Tran24] and the references therein.
Several of the approaches suggested so far have turned out to be cumbersome, if not unfeasible, with respect to theoretical investigations, and only simulation studies can be performed. In [Reference Nagel and Weiß21] the STIT (STable with respect to ITerations) tessellation process was introduced, which is a cell division process allowing for numerous theoretical results; see, for example, [Reference Martínez and Nagel15, Reference Mecke, Nagel and Weiss17, Reference Mecke, Nagel and Weiss18, Reference Nagel and Weiß22, Reference Schreiber and Thäle26–Reference Schreiber and Thäle28]. Due to its nice mathematical properties, it can be considered as a reference model for fracture patterns. On the other hand, some statistical goodness-of-fit checks indicate the need for modification and adaption of the STIT model, see [Reference León, Nagel, Ohser and Arscott12, Reference Nagel, Mecke, Ohser and Weiß20]. This motivates the present paper.
Our work is essentially inspired by [Reference Cowan3], where a systematic approach to a wide class of cell division processes is provided by introducing ‘selection rules’—in the present paper adapted as ‘life time distributions’—and ‘division rules’.
In [Reference Georgii, Schreiber and Thäle4, Reference Schreiber and Thäle29] a theoretical base for generalizations of the STIT model was provided. In those papers the focus was on modifications of the division rules for the cells.
Our purpose is the construction of tessellation-valued cell division processes in the d-dimensional Euclidean space
![]() $\mathbb{R}^d$
, where the life time distributions of the cells differ from those for the STIT model. We provide sufficient conditions and a rigorous proof of their existence, which is a critical issue for such models, and study some of their features.
$\mathbb{R}^d$
, where the life time distributions of the cells differ from those for the STIT model. We provide sufficient conditions and a rigorous proof of their existence, which is a critical issue for such models, and study some of their features.
The idea of the proof of Theorem 1 is based on the ‘global construction’ of STIT tessellations in [Reference Mecke, Nagel and Weiss18]. For this reason, the models we consider all have the same division rule like the STIT tessellation, driven by a translation-invariant hyperplane measure. The new results of this paper concern a variety of life time distributions of the cells.
In Section 3 we start with a proof of the tail triviality of the zero-cell process of a Poisson hyperplane tessellation process. Because this process of zero-cells plays a central role in several proofs of cell division processes, this is a result of independent interest. Then, in Section 4, a sufficient condition for the existence of a class of cell division processes is provided together with their construction. Several more concrete results are shown in Section 5 for the particular case of the so-called Mondrian model where all the tessellation cells are cuboids. We conclude by describing a link between a particular cell division process in a bounded window and a fragmentation. Fragmentation models as introduced and studied in [Reference Bertoin1] (for a definition, see Section 1.1.3 therein) are such that at any time there is a countable class of particles of sizes
![]() $(s_i\colon i \in \mathbb{N})$
evolving independently. At the end of its life a particle of size
$(s_i\colon i \in \mathbb{N})$
evolving independently. At the end of its life a particle of size
![]() $s_i$
splits into a sequence of fragments of sizes
$s_i$
splits into a sequence of fragments of sizes
![]() $(s_{i,j}\colon j\in \mathbb{N})$
such that the law of the ratios of the sizes of the split fragments with respect to the size of the original fragment (that is, the law of
$(s_{i,j}\colon j\in \mathbb{N})$
such that the law of the ratios of the sizes of the split fragments with respect to the size of the original fragment (that is, the law of
![]() $(s_{i,j}/s_i\colon j\in \mathbb{N})$
) does not depend on the size
$(s_{i,j}/s_i\colon j\in \mathbb{N})$
) does not depend on the size
![]() $s_i$
. The lifetime of a particle of size
$s_i$
. The lifetime of a particle of size
![]() $s_i$
is exponentially distributed with a parameter of order
$s_i$
is exponentially distributed with a parameter of order
![]() $s_i^\alpha$
, and
$s_i^\alpha$
, and
![]() $\alpha$
is called the index of self-similarity. In Section 5.3 we discuss conditions that a cell size function G must satisfy in order that a random tessellation resulting from an (L-G) (D-
$\alpha$
is called the index of self-similarity. In Section 5.3 we discuss conditions that a cell size function G must satisfy in order that a random tessellation resulting from an (L-G) (D-
![]() $\Lambda$
) cell division process corresponds to such a fragmentation.
$\Lambda$
) cell division process corresponds to such a fragmentation.
2. Notation
By
![]() $\mathbb{R}^d$
we denote the d-dimensional Euclidean space,
$\mathbb{R}^d$
we denote the d-dimensional Euclidean space,
![]() $d\geq 1$
, with the scalar product
$d\geq 1$
, with the scalar product
![]() $\langle \cdot ,\cdot \rangle$
. The origin is o, and
$\langle \cdot ,\cdot \rangle$
. The origin is o, and
![]() $S^{d-1}$
is the unit sphere with the Borel
$S^{d-1}$
is the unit sphere with the Borel
![]() $\sigma$
-algebra
$\sigma$
-algebra
![]() ${\mathcal B} (S^{d-1})$
. Denote by
${\mathcal B} (S^{d-1})$
. Denote by
![]() ${\sf B}_r$
the ball centered at the origin o with radius
${\sf B}_r$
the ball centered at the origin o with radius
![]() $r>0$
. The topological interior of a set
$r>0$
. The topological interior of a set
![]() $A\subseteq \mathbb{R}^d$
is
$A\subseteq \mathbb{R}^d$
is
![]() $\textrm{int} (A)$
. The Lebesgue measure on
$\textrm{int} (A)$
. The Lebesgue measure on
![]() $\mathbb{R}$
is denoted by
$\mathbb{R}$
is denoted by
![]() $\lambda$
. The set of the nonnegative integers is
$\lambda$
. The set of the nonnegative integers is
![]() $\mathbb{N}_0$
,
$\mathbb{N}_0$
,
![]() $\mathbb{Z}$
denotes the set of integers, and
$\mathbb{Z}$
denotes the set of integers, and
![]() $\mathbb{Z}_- :\!=\{ i\in \mathbb{Z} \colon i\leq 0\}$
. The symbol
$\mathbb{Z}_- :\!=\{ i\in \mathbb{Z} \colon i\leq 0\}$
. The symbol
![]() $\stackrel{\textrm{D}}{=}$
means the identity of distributions of two random variables. We use the abbreviation ‘i.i.d.’ for ‘independent and identically distributed’ random variables.
$\stackrel{\textrm{D}}{=}$
means the identity of distributions of two random variables. We use the abbreviation ‘i.i.d.’ for ‘independent and identically distributed’ random variables.
Let
![]() $\mathcal{H} $
denote the set of all hyperplanes in
$\mathcal{H} $
denote the set of all hyperplanes in
![]() $\mathbb{R}^d$
, endowed with the Borel
$\mathbb{R}^d$
, endowed with the Borel
![]() $\sigma$
-algebra associated with the Fell topology. For a hyperplane
$\sigma$
-algebra associated with the Fell topology. For a hyperplane
![]() $h\in \mathcal{H}$
we use the parametrization
$h\in \mathcal{H}$
we use the parametrization
![]() $h(u,x):\!= \{ y\in \mathbb{R}^d\colon \langle y,u\rangle =x\}$
,
$h(u,x):\!= \{ y\in \mathbb{R}^d\colon \langle y,u\rangle =x\}$
,
![]() $u\in S^{d-1}$
,
$u\in S^{d-1}$
,
![]() $x\in \mathbb{R}$
. Note, that
$x\in \mathbb{R}$
. Note, that
![]() $h(u,x)=h(\!{-}u,-x)$
, and thus all hyperplanes can be parametrized in two different ways. Denote by
$h(u,x)=h(\!{-}u,-x)$
, and thus all hyperplanes can be parametrized in two different ways. Denote by
![]() $[B]:\!= \{ h\in \mathcal{H} \colon h\cap B \not= \emptyset \}$
the set of all hyperplanes that intersect the set
$[B]:\!= \{ h\in \mathcal{H} \colon h\cap B \not= \emptyset \}$
the set of all hyperplanes that intersect the set
![]() $B \subset \mathbb{R}^d$
.
$B \subset \mathbb{R}^d$
.
Let
![]() $\varphi$
denote an even probability measure on
$\varphi$
denote an even probability measure on
![]() $S^{d-1}$
, which is a probability measure on
$S^{d-1}$
, which is a probability measure on
![]() $S^{d-1}$
with
$S^{d-1}$
with
![]() $\varphi (A)=\varphi (\!{-}A)$
for all
$\varphi (A)=\varphi (\!{-}A)$
for all
![]() $A\in {\mathcal B} (S^{d-1})$
.
$A\in {\mathcal B} (S^{d-1})$
.
Throughout this paper we use a translation-invariant measure
![]() $\Lambda$
on
$\Lambda$
on
![]() $\mathcal{H}$
which satisfies
$\mathcal{H}$
which satisfies
for all nonnegative measurable functions
![]() $f\colon\mathcal{H} \to \mathbb{R}$
. The probability measure
$f\colon\mathcal{H} \to \mathbb{R}$
. The probability measure
![]() $\varphi$
is called the spherical directional distribution. We need a further assumption on
$\varphi$
is called the spherical directional distribution. We need a further assumption on
![]() $\varphi$
which guarantees that the constructed structures are indeed tessellations with bounded cells, see [Reference Schneider and Weil25, p. 486]:
$\varphi$
which guarantees that the constructed structures are indeed tessellations with bounded cells, see [Reference Schneider and Weil25, p. 486]:
A great subsphere is the intersection of
![]() $S^{d-1}$
with a hyperplane through the origin. Condition (2) is equivalent to the assumption that there is no line in
$S^{d-1}$
with a hyperplane through the origin. Condition (2) is equivalent to the assumption that there is no line in
![]() $\mathbb{R}^d$
with which
$\mathbb{R}^d$
with which
![]() $\varphi$
-almost-all hyperplanes are parallel.
$\varphi$
-almost-all hyperplanes are parallel.
A polytope in
![]() $\mathbb{R}^d$
is the convex hull of a nonempty finite set of points. By
$\mathbb{R}^d$
is the convex hull of a nonempty finite set of points. By
![]() ${\mathcal{P}_d}$
we denote the set of all d-dimensional polytopes in
${\mathcal{P}_d}$
we denote the set of all d-dimensional polytopes in
![]() $\mathbb{R}^d$
.
$\mathbb{R}^d$
.
Definition 1. A tessellation of
![]() $\mathbb{R}^d$
is a countable set
$\mathbb{R}^d$
is a countable set
![]() $T\subset{\mathcal{P}_d}$
of d-dimensional polytopes satisfying the following conditions:
$T\subset{\mathcal{P}_d}$
of d-dimensional polytopes satisfying the following conditions:
-
(i)
 ${\bigcup_{z\in T} z = \mathbb{R}^d}$
(covering);
${\bigcup_{z\in T} z = \mathbb{R}^d}$
(covering); -
(ii) if
 $z,z^{\prime}\in T$
and
$z,z^{\prime}\in T$
and
 $z\not= z^{\prime}$
, then
$z\not= z^{\prime}$
, then
 $\textrm{int}(z)\cap \textrm{int}(z^{\prime})= \emptyset$
(disjoint interiors);
$\textrm{int}(z)\cap \textrm{int}(z^{\prime})= \emptyset$
(disjoint interiors); -
(iii) the set
 $\{ z\in T\colon z\cap C \not= \emptyset\}$
is finite for all compact sets
$\{ z\in T\colon z\cap C \not= \emptyset\}$
is finite for all compact sets
 $C\subset\mathbb{R}^d$
(local finiteness).
$C\subset\mathbb{R}^d$
(local finiteness).
The polytopes
![]() $z\in T$
are referred to as the cells of T.
$z\in T$
are referred to as the cells of T.
Let
![]() $\mathbb{T}$
denote the set of all tessellations of
$\mathbb{T}$
denote the set of all tessellations of
![]() $\mathbb{R}^d$
, endowed with the usual
$\mathbb{R}^d$
, endowed with the usual
![]() $\sigma$
-algebra, which is associated with the Borel
$\sigma$
-algebra, which is associated with the Borel
![]() $\sigma$
-algebra for the Fell topology in the space of closed subsets of
$\sigma$
-algebra for the Fell topology in the space of closed subsets of
![]() $\mathbb{R}^d$
, using that the union of cell boundaries
$\mathbb{R}^d$
, using that the union of cell boundaries
![]() $\partial T :\!= \bigcup_{z\in T} \partial z$
, also referred to as the
$\partial T :\!= \bigcup_{z\in T} \partial z$
, also referred to as the
![]() $(d-1)$
-skeleton, of a tessellation T is a closed subset of
$(d-1)$
-skeleton, of a tessellation T is a closed subset of
![]() $\mathbb{R}^d$
. A random tessellation is a measurable mapping from a probability space to
$\mathbb{R}^d$
. A random tessellation is a measurable mapping from a probability space to
![]() $\mathbb{T}$
.
$\mathbb{T}$
.
For more details on the definition of random tessellation we refer to [Reference Schneider and Weil25].
In this paper, Poisson point processes are used extensively. For this, we refer to [Reference Last and Penrose9], and in particular Chapters 5 and 7 therein.
3. An auxiliary Poisson process of hyperplanes marked with birth times, and the process of zero-cells
Let
![]() $\Lambda$
be a translation-invariant measure on the space
$\Lambda$
be a translation-invariant measure on the space
![]() $\mathcal{H} $
of hyperplanes in
$\mathcal{H} $
of hyperplanes in
![]() $\mathbb{R}^d$
, satisfying (1) and (2). We denote by
$\mathbb{R}^d$
, satisfying (1) and (2). We denote by
![]() $\hat X^*$
a Poisson point process on
$\hat X^*$
a Poisson point process on
![]() $\mathcal{H} \times (0,\infty)$
with the intensity measure
$\mathcal{H} \times (0,\infty)$
with the intensity measure
![]() $\Lambda \otimes \lambda_+$
, where
$\Lambda \otimes \lambda_+$
, where
![]() $\lambda_+$
is the Lebesgue measure on
$\lambda_+$
is the Lebesgue measure on
![]() $(0,\infty)$
. If
$(0,\infty)$
. If
![]() $(h,t)\in \hat X^*$
, we interpret this as a hyperplane with birth time t. Furthermore, define
$(h,t)\in \hat X^*$
, we interpret this as a hyperplane with birth time t. Furthermore, define
![]() $\hat X^*_t :\!= \{(h,t^{\prime})\in \hat X^*\colon t^{\prime}\leq t\}$
and
$\hat X^*_t :\!= \{(h,t^{\prime})\in \hat X^*\colon t^{\prime}\leq t\}$
and
![]() $\hat X_t :\!= \{h\in \mathcal{H}\colon \textrm{there exists}\ (h,t^{\prime})\in X^*_t\}$
. Now we can introduce the process
$\hat X_t :\!= \{h\in \mathcal{H}\colon \textrm{there exists}\ (h,t^{\prime})\in X^*_t\}$
. Now we can introduce the process
![]() $(\tilde z^o_t ,\, t>0)$
, where
$(\tilde z^o_t ,\, t>0)$
, where
![]() $\tilde z^o_t$
is the zero-cell (that is, the cell containing the origin o) of the Poisson hyperplane tessellation of
$\tilde z^o_t$
is the zero-cell (that is, the cell containing the origin o) of the Poisson hyperplane tessellation of
![]() $\mathbb{R}^d$
induced by
$\mathbb{R}^d$
induced by
![]() $\hat X_t$
. The process
$\hat X_t$
. The process
![]() $(\tilde z^o_t ,\, t>0)$
is a pure jump Markov process, with
$(\tilde z^o_t ,\, t>0)$
is a pure jump Markov process, with
![]() $\tilde z^o_{t^{\prime}} \subseteq \tilde z^o_{t}$
if
$\tilde z^o_{t^{\prime}} \subseteq \tilde z^o_{t}$
if
![]() $t<t^{\prime}$
. And, most importantly,
$t<t^{\prime}$
. And, most importantly,
Denote by
![]() $(t_i ,\, i \in \mathbb{Z} )$
the ordered sequence of jump times of
$(t_i ,\, i \in \mathbb{Z} )$
the ordered sequence of jump times of
![]() $(\tilde z^o_t ,\, t>0)$
with
$(\tilde z^o_t ,\, t>0)$
with
![]() $t_0<1<t_1$
. Correspondingly,
$t_0<1<t_1$
. Correspondingly,
![]() $(h_i, t_i)\in \hat X^*$
are the time-marked dividing hyperplanes causing a jump of
$(h_i, t_i)\in \hat X^*$
are the time-marked dividing hyperplanes causing a jump of
![]() $(\tilde z^o_t , t>0)$
.
$(\tilde z^o_t , t>0)$
.
Denote by
the sequence of zero cells with
![]() $\tilde z^o_{(i)}:\!=\tilde z^o_{t_i}$
.
$\tilde z^o_{(i)}:\!=\tilde z^o_{t_i}$
.
Consider the process
![]() $(\hat z_n ,\, n\in \mathbb{N}_0)$
with
$(\hat z_n ,\, n\in \mathbb{N}_0)$
with
![]() $\hat z_n:\!= \tilde z^o_{(\!{-}n)}$
, and denote by
$\hat z_n:\!= \tilde z^o_{(\!{-}n)}$
, and denote by
![]() $\mathcal{F}_n :\!= \sigma (\hat z_n)$
,
$\mathcal{F}_n :\!= \sigma (\hat z_n)$
,
![]() $n\in \mathbb{N}_0$
, the
$n\in \mathbb{N}_0$
, the
![]() $\sigma$
-algebra generated by
$\sigma$
-algebra generated by
![]() $\hat z_n$
. The tail-
$\hat z_n$
. The tail-
![]() $\sigma$
-algebra is then
$\sigma$
-algebra is then
![]() $\mathcal{F}_\infty :\!= \bigcap_{m\in \mathbb{N}_0}\bigvee_{k\geq m} \mathcal{F}_k $
, where
$\mathcal{F}_\infty :\!= \bigcap_{m\in \mathbb{N}_0}\bigvee_{k\geq m} \mathcal{F}_k $
, where
![]() $\bigvee$
stands for the
$\bigvee$
stands for the
![]() $\sigma$
-algebra generated by the union of the respective
$\sigma$
-algebra generated by the union of the respective
![]() $\sigma$
-algebras.
$\sigma$
-algebras.
Lemma 1.
The tail-
![]() $\sigma$
-algebra
$\sigma$
-algebra
![]() $\mathcal{F}_\infty$
of the process
$\mathcal{F}_\infty$
of the process
![]() $(\hat z_n,\, n\in \mathbb{N}_0)$
is trivial, i.e.
$(\hat z_n,\, n\in \mathbb{N}_0)$
is trivial, i.e.
![]() $\mathbb{P}(B)\in \{ 0,1\}$
for all
$\mathbb{P}(B)\in \{ 0,1\}$
for all
![]() $B\in \mathcal{F}_\infty $
.
$B\in \mathcal{F}_\infty $
.
Proof. Let
![]() $B\in \mathcal{F}_\infty$
and
$B\in \mathcal{F}_\infty$
and
![]() ${\varepsilon} >0$
be fixed. Then there are an
${\varepsilon} >0$
be fixed. Then there are an
![]() $m\in\mathbb{N}$
and a
$m\in\mathbb{N}$
and a
![]() $B_m \in \bigvee_{k\leq m} \mathcal{F}_k$
such that
$B_m \in \bigvee_{k\leq m} \mathcal{F}_k$
such that
![]() $\mathbb{P}(B\Delta B_m )<{\varepsilon}$
[Reference Halmos6, Theorem D, Chapter III]. In the following we consider m and
$\mathbb{P}(B\Delta B_m )<{\varepsilon}$
[Reference Halmos6, Theorem D, Chapter III]. In the following we consider m and
![]() $B_m$
as fixed.
$B_m$
as fixed.
The main idea of the proof is to construct times
![]() ${\tilde t} < t^*$
, two polytopes
${\tilde t} < t^*$
, two polytopes
![]() $W^{\prime}\subset W$
containing the origin o, and events E,
$W^{\prime}\subset W$
containing the origin o, and events E,
![]() $E_m$
, A,
$E_m$
, A,
![]() $A_n$
,
$A_n$
,
![]() $n>m$
, such that
$n>m$
, such that
the event
 $E\cap E_m$
implies that
$E\cap E_m$
implies that
 $W^{\prime}\subseteq \hat z_m \subseteq W$
, and that the jump time
$W^{\prime}\subseteq \hat z_m \subseteq W$
, and that the jump time
 $t_{-m}\geq t^*$
;
$t_{-m}\geq t^*$
;the event
 $A\cap A_n$
implies that
$A\cap A_n$
implies that
 $W \subseteq \hat z_n$
, and that the jump time
$W \subseteq \hat z_n$
, and that the jump time
 $t_{-n}\leq {\tilde t}$
.
$t_{-n}\leq {\tilde t}$
.
For
![]() $W^{\prime}, W\in {\mathcal{P}_d}$
,
$W^{\prime}, W\in {\mathcal{P}_d}$
,
![]() $W^{\prime}\subset W$
, with the origin o in the interior of W
$W^{\prime}\subset W$
, with the origin o in the interior of W
![]() $^{\prime}$
, define the time
$^{\prime}$
, define the time
![]() $S(W^{\prime},W):\!= \inf \{ t>0\colon W^{\prime} \subset \tilde z^o_t \subset W \}$
, which is the time of first separation of the boundary of W
$S(W^{\prime},W):\!= \inf \{ t>0\colon W^{\prime} \subset \tilde z^o_t \subset W \}$
, which is the time of first separation of the boundary of W
![]() $^{\prime}$
from the boundary of W by the boundary of the zero-cell, introduced in [Reference Martínez and Nagel14] as the ‘encapsulation time’.
$^{\prime}$
from the boundary of W by the boundary of the zero-cell, introduced in [Reference Martínez and Nagel14] as the ‘encapsulation time’.
For
![]() $t^* \in (0,1)$
and
$t^* \in (0,1)$
and
![]() $r>0$
, define the intervals
$r>0$
, define the intervals
![]() $a_i:\!=((i-1){r}/{m},i{r}/{m})$
of length
$a_i:\!=((i-1){r}/{m},i{r}/{m})$
of length
![]() $r/m$
, and time intervals
$r/m$
, and time intervals
![]() $\Delta_i :\!=(t^* + (i-1)({1-t^*})/{m} , t^* + i({1-t^*})/{m})$
of length
$\Delta_i :\!=(t^* + (i-1)({1-t^*})/{m} , t^* + i({1-t^*})/{m})$
of length
![]() $(1-t^*)/m$
between
$(1-t^*)/m$
between
![]() $t^*$
and 1,
$t^*$
and 1,
![]() $i\in \{ 1,\ldots ,m\}$
.
$i\in \{ 1,\ldots ,m\}$
.
Now, for
![]() $m\in\mathbb{N}$
and
$m\in\mathbb{N}$
and
![]() ${\varepsilon}>0$
choose a pair
${\varepsilon}>0$
choose a pair
![]() $(t^*,r)\in(0,1)\times(0,\infty)$
such that, for the event
$(t^*,r)\in(0,1)\times(0,\infty)$
such that, for the event
 \begin{align*} E_m & :\!= \{\hat X^*\cap(\{h(u,x)\in\mathcal{H}\colon x\in(\!{-}r,r),\,u\in S^{d-1}\}\times (0,t^*))=\emptyset\} \\ & \quad\ \cap \bigcap_{i=1}^m\{\hat X^*\cap(\{h(u,x)\in\mathcal{H}\colon x\in a_i\cup(\!{-}a_i),\, u\in S^{d-1}\}\times\Delta_i) \not= \emptyset\}, \end{align*}
\begin{align*} E_m & :\!= \{\hat X^*\cap(\{h(u,x)\in\mathcal{H}\colon x\in(\!{-}r,r),\,u\in S^{d-1}\}\times (0,t^*))=\emptyset\} \\ & \quad\ \cap \bigcap_{i=1}^m\{\hat X^*\cap(\{h(u,x)\in\mathcal{H}\colon x\in a_i\cup(\!{-}a_i),\, u\in S^{d-1}\}\times\Delta_i) \not= \emptyset\}, \end{align*}
we have
This can be realized by choosing
![]() $r>-({m^2}/{2})\ln(1-(1-{\varepsilon})^{{1}/{2m}})$
and then
$r>-({m^2}/{2})\ln(1-(1-{\varepsilon})^{{1}/{2m}})$
and then
![]() $t^* < - ({1}/{2r}) \ln (1-{\varepsilon})$
, which guarantees that each of the two factors is greater than
$t^* < - ({1}/{2r}) \ln (1-{\varepsilon})$
, which guarantees that each of the two factors is greater than
![]() $\sqrt{1-{\varepsilon}}$
.
$\sqrt{1-{\varepsilon}}$
.
The event
![]() $E_m$
means that the ball
$E_m$
means that the ball
![]() ${\sf B}_r$
is not intersected by a hyperplane of
${\sf B}_r$
is not intersected by a hyperplane of
![]() $\hat X^*$
until time
$\hat X^*$
until time
![]() $t^*$
, and then in each of the m time intervals
$t^*$
, and then in each of the m time intervals
![]() $\Delta_i :\!=(t^*+(i-1)({1-t^*})/{m},t^*+i({1-t^*})/{m})$
of length
$\Delta_i :\!=(t^*+(i-1)({1-t^*})/{m},t^*+i({1-t^*})/{m})$
of length
![]() $(1-t^*)/m$
between
$(1-t^*)/m$
between
![]() $t^*$
and 1 there is at least one hyperplane of
$t^*$
and 1 there is at least one hyperplane of
![]() $\hat X^*$
with a distance to the origin in the interval
$\hat X^*$
with a distance to the origin in the interval
![]() $a_i:\!=((i-1){r}/{m},i{r}/{m})$
,
$a_i:\!=((i-1){r}/{m},i{r}/{m})$
,
![]() $i\in \{ 1,\ldots ,m\}$
. This guarantees that there are at least m jumps of the zero-cell process in the time interval
$i\in \{ 1,\ldots ,m\}$
. This guarantees that there are at least m jumps of the zero-cell process in the time interval
![]() $(t^* ,1)$
.
$(t^* ,1)$
.
The pair
![]() $(t^*, r)$
is now considered to be fixed. Choose
$(t^*, r)$
is now considered to be fixed. Choose
![]() $W^{\prime}\in {\mathcal{P}_d}$
such that
$W^{\prime}\in {\mathcal{P}_d}$
such that
![]() ${\sf B}_r \subset W^{\prime}$
. By [Reference Martínez and Nagel14, Lemma 5], there exists a
${\sf B}_r \subset W^{\prime}$
. By [Reference Martínez and Nagel14, Lemma 5], there exists a
![]() $W\in {\mathcal{P}_d}$
with
$W\in {\mathcal{P}_d}$
with
![]() $W^{\prime}\subset W$
such that, for the event
$W^{\prime}\subset W$
such that, for the event
![]() $E:\!=\{S(W^{\prime},W)<t^*\}$
,
$E:\!=\{S(W^{\prime},W)<t^*\}$
,
![]() $\mathbb{P}(E) =\mathbb{P}(S(W^{\prime},W)<t^*)>1-{\varepsilon}$
.
$\mathbb{P}(E) =\mathbb{P}(S(W^{\prime},W)<t^*)>1-{\varepsilon}$
.
From now on, W is also considered to be fixed. Furthermore, choose
![]() ${\tilde t}\in (0,t^*)$
such that, for the event
${\tilde t}\in (0,t^*)$
such that, for the event
![]() $A:\!=\{ [W] \cap \hat X_{{\tilde t}} =\emptyset\}$
, which means that at time
$A:\!=\{ [W] \cap \hat X_{{\tilde t}} =\emptyset\}$
, which means that at time
![]() $\tilde t$
the window W is contained in the zero-cell,
$\tilde t$
the window W is contained in the zero-cell,
![]() $\mathbb{P}(A)=\exp(\!{-}{\tilde t}\, \Lambda ([W])) >1-{\varepsilon}$
. Then, having fixed
$\mathbb{P}(A)=\exp(\!{-}{\tilde t}\, \Lambda ([W])) >1-{\varepsilon}$
. Then, having fixed
![]() $\tilde t$
, choose
$\tilde t$
, choose
![]() $n>m$
such that, for the event
$n>m$
such that, for the event
![]() $A_n$
, in the time interval
$A_n$
, in the time interval
![]() $(\tilde t , 1)$
at most n hyperplanes of
$(\tilde t , 1)$
at most n hyperplanes of
![]() $\hat X^*$
intersect W,
$\hat X^*$
intersect W,
Note that
![]() $A\cap A_n \subseteq \{ W\subseteq \hat z_n\}$
.
$A\cap A_n \subseteq \{ W\subseteq \hat z_n\}$
.
By the characteristic property of Poisson point processes, the restricted point processes on disjoint sets, namely
![]() $\hat X^* \cap ([W] \times (t^*,1))$
and
$\hat X^* \cap ([W] \times (t^*,1))$
and
![]() $\hat X^* \cap ([W]^\textrm{c} \times (0,{\tilde t}))$
, are independent. Hence, for
$\hat X^* \cap ([W]^\textrm{c} \times (0,{\tilde t}))$
, are independent. Hence, for
![]() $B_m \in \bigvee_{k\leq m} \mathcal{F}_k $
,
$B_m \in \bigvee_{k\leq m} \mathcal{F}_k $
,
![]() $C \in \bigvee_{k\geq n} \mathcal{F}_k $
, and with
$C \in \bigvee_{k\geq n} \mathcal{F}_k $
, and with
![]() $D:\!=E\cap E_m \cap A \cap A_n$
, the events
$D:\!=E\cap E_m \cap A \cap A_n$
, the events
![]() $B_m$
and C are conditionally independent under the condition D, and thus
$B_m$
and C are conditionally independent under the condition D, and thus
With the construction and the assumptions on the events above, we have
![]() $\mathbb{P}(D)>1-4{\varepsilon}$
, and this yields
$\mathbb{P}(D)>1-4{\varepsilon}$
, and this yields
![]() $(\mathbb{P}(B_m )-4{\varepsilon} ) (\mathbb{P}(C)- 4{\varepsilon} )\leq \mathbb{P}(B_m \cap D) \mathbb{P}(C\cap D)\leq \mathbb{P}(B_m ) \mathbb{P}(C)$
. Furthermore,
$(\mathbb{P}(B_m )-4{\varepsilon} ) (\mathbb{P}(C)- 4{\varepsilon} )\leq \mathbb{P}(B_m \cap D) \mathbb{P}(C\cap D)\leq \mathbb{P}(B_m ) \mathbb{P}(C)$
. Furthermore,
![]() $(1-4{\varepsilon} )\mathbb{P}(B_m ) \mathbb{P}(C)\leq \mathbb{P}(B_m ) \mathbb{P}(C) \mathbb{P}(D) \leq \mathbb{P}(B_m )\mathbb{P}(C)$
, and also
$(1-4{\varepsilon} )\mathbb{P}(B_m ) \mathbb{P}(C)\leq \mathbb{P}(B_m ) \mathbb{P}(C) \mathbb{P}(D) \leq \mathbb{P}(B_m )\mathbb{P}(C)$
, and also
![]() $\mathbb{P}(B_m\cap C\cap D^\textrm{c}) \leq \mathbb{P}(D^\textrm{c})<4{\varepsilon}$
. Hence, for
$\mathbb{P}(B_m\cap C\cap D^\textrm{c}) \leq \mathbb{P}(D^\textrm{c})<4{\varepsilon}$
. Hence, for
![]() ${\varepsilon} <1/4$
,
${\varepsilon} <1/4$
,
 \begin{align*} \frac{1}{\mathbb{P}(D)} & |\mathbb{P}(B_m\cap D)\mathbb{P}(C\cap D)-\mathbb{P}(B_m)\mathbb{P}(C)\mathbb{P}(D)| + \mathbb{P}(B_m\cap C\cap D^\textrm{c}) \\ & < \frac{1}{1-4{\varepsilon}}\max\{\mathbb{P}(B_m )\mathbb{P}(C)(1-(1-4{\varepsilon})), 4{\varepsilon} (\mathbb{P}(B_m)+\mathbb{P}(C))-16{\varepsilon}^2)\} + 4{\varepsilon} \\ & \leq \frac{\max\{4{\varepsilon},8{\varepsilon}-16{\varepsilon}^2\}+4{\varepsilon}-16{\varepsilon}^2} {1-4{\varepsilon}} \leq \frac{12 {\varepsilon} }{1-4{\varepsilon}}. \end{align*}
\begin{align*} \frac{1}{\mathbb{P}(D)} & |\mathbb{P}(B_m\cap D)\mathbb{P}(C\cap D)-\mathbb{P}(B_m)\mathbb{P}(C)\mathbb{P}(D)| + \mathbb{P}(B_m\cap C\cap D^\textrm{c}) \\ & < \frac{1}{1-4{\varepsilon}}\max\{\mathbb{P}(B_m )\mathbb{P}(C)(1-(1-4{\varepsilon})), 4{\varepsilon} (\mathbb{P}(B_m)+\mathbb{P}(C))-16{\varepsilon}^2)\} + 4{\varepsilon} \\ & \leq \frac{\max\{4{\varepsilon},8{\varepsilon}-16{\varepsilon}^2\}+4{\varepsilon}-16{\varepsilon}^2} {1-4{\varepsilon}} \leq \frac{12 {\varepsilon} }{1-4{\varepsilon}}. \end{align*}
Because
![]() $B\in \mathcal{F}_\infty \subseteq \bigvee_{k\geq n} \mathcal{F}_k$
, we have
$B\in \mathcal{F}_\infty \subseteq \bigvee_{k\geq n} \mathcal{F}_k$
, we have
![]() $|\mathbb{P}(B_m\cap B)-\mathbb{P}(B_m)\mathbb{P}(B)|<{12{\varepsilon}}/({1-4{\varepsilon}})$
. Then,
$|\mathbb{P}(B_m\cap B)-\mathbb{P}(B_m)\mathbb{P}(B)|<{12{\varepsilon}}/({1-4{\varepsilon}})$
. Then,
![]() $\mathbb{P} (B\Delta B_m )<{\varepsilon}$
yields
$\mathbb{P} (B\Delta B_m )<{\varepsilon}$
yields
![]() $|\mathbb{P}(B\cap B)-\mathbb{P}(B)\mathbb{P}(B)|<{12{\varepsilon}}/({1-4{\varepsilon}})+2{\varepsilon}$
for all
$|\mathbb{P}(B\cap B)-\mathbb{P}(B)\mathbb{P}(B)|<{12{\varepsilon}}/({1-4{\varepsilon}})+2{\varepsilon}$
for all
![]() ${\varepsilon} >0$
, and hence
${\varepsilon} >0$
, and hence
![]() $P(B)=0$
or 1.
$P(B)=0$
or 1.
The tail triviality of the zero-cell process is now used to show further 0–1 probabilities. The following assertion will be applied in the proof of Theorem 1.
Corollary 1.
Let
![]() $\Lambda$
be a translation-invariant measure on the space of hyperplanes in
$\Lambda$
be a translation-invariant measure on the space of hyperplanes in
![]() $\mathbb{R}^d$
, satisfying (1) and (2), and let
$\mathbb{R}^d$
, satisfying (1) and (2), and let
![]() $G\colon {\mathcal{P}_d} \to [0,\infty )$
be a measurable functional on the set of d-dimensional polytopes. Then
$G\colon {\mathcal{P}_d} \to [0,\infty )$
be a measurable functional on the set of d-dimensional polytopes. Then
Let
![]() $(\tau^{\prime}_i,\, i\in \mathbb{Z})$
be a sequence of i.i.d. random variables, independent of
$(\tau^{\prime}_i,\, i\in \mathbb{Z})$
be a sequence of i.i.d. random variables, independent of
![]() $\hat X^*$
. Then
$\hat X^*$
. Then
Proof. By the measurability of G, the event
![]() $\big\{\text{there exists }m\in\mathbb{Z}\colon\sum_{i\leq m}G\big(\tilde z^o_{(i)}\big)^{-1}<\infty\big\}$
is an element of the tail-
$\big\{\text{there exists }m\in\mathbb{Z}\colon\sum_{i\leq m}G\big(\tilde z^o_{(i)}\big)^{-1}<\infty\big\}$
is an element of the tail-
![]() $\sigma$
-algebra
$\sigma$
-algebra
![]() $\mathcal{F}_\infty$
, and we can apply Lemma 1.
$\mathcal{F}_\infty$
, and we can apply Lemma 1.
If
![]() $(\tau^{\prime}_i,\, i\in \mathbb{Z})$
is a sequence of i.i.d. random variables that is independent of
$(\tau^{\prime}_i,\, i\in \mathbb{Z})$
is a sequence of i.i.d. random variables that is independent of
![]() $\hat X^*$
, then this result can be extended straightforwardly to the product-
$\hat X^*$
, then this result can be extended straightforwardly to the product-
![]() $\sigma$
-algebras
$\sigma$
-algebras
![]() $\mathcal{F}_n \otimes \mathcal{F}_n^\tau$
,
$\mathcal{F}_n \otimes \mathcal{F}_n^\tau$
,
![]() $n\in \mathbb{N}_0$
, where
$n\in \mathbb{N}_0$
, where
![]() $\mathcal{F}_n :\!= \sigma (\hat z_n)$
,
$\mathcal{F}_n :\!= \sigma (\hat z_n)$
,
![]() $n\in \mathbb{N}_0$
, and
$n\in \mathbb{N}_0$
, and
![]() $\mathcal{F}_n^\tau:\!= \sigma (\tau_n)$
. This yields (6).
$\mathcal{F}_n^\tau:\!= \sigma (\tau_n)$
. This yields (6).
To prove (7), first note that almost sure non-explosion of the process
![]() $\big(\sum_{-j\leq i\leq m}G\big(\tilde z^o_{(i)}\big)^{-1}\tau^{\prime}_i$
,
$\big(\sum_{-j\leq i\leq m}G\big(\tilde z^o_{(i)}\big)^{-1}\tau^{\prime}_i$
,
![]() $j\in\mathbb{N}\big)$
means that
$j\in\mathbb{N}\big)$
means that
![]() $\mathbb{P}\big(\sum_{i\leq m}G\big(\tilde z^o_{(i)}\big)^{-1}\tau^{\prime}_i=\infty\big)=1$
. It is well known in the theory of birth processes (see, for example, [Reference Kallenberg7, Proposition 13.5]) that this is equivalent to
$\mathbb{P}\big(\sum_{i\leq m}G\big(\tilde z^o_{(i)}\big)^{-1}\tau^{\prime}_i=\infty\big)=1$
. It is well known in the theory of birth processes (see, for example, [Reference Kallenberg7, Proposition 13.5]) that this is equivalent to
![]() $\mathbb{P}\big(\sum_{i\leq m}G\big(\tilde z^o_{(i)}\big)^{-1} = \infty\big)=1$
, which means that the property of non-explosion only depends on the series of the expectations
$\mathbb{P}\big(\sum_{i\leq m}G\big(\tilde z^o_{(i)}\big)^{-1} = \infty\big)=1$
, which means that the property of non-explosion only depends on the series of the expectations
![]() $G\big(\tilde z^o_{(i)}\big)^{-1}$
of the holding times of the respective states of the process. Hence, for the respective complements,
$G\big(\tilde z^o_{(i)}\big)^{-1}$
of the holding times of the respective states of the process. Hence, for the respective complements,
Because, by (5) and (6), both probabilities can have the values 0 or 1 only, we obtain (7).
In [Reference Martnez and Nagel16], the rescaled time-stationary process of zero-cells
![]() $(a^t \tilde z^o_{a^t},\, t\in \mathbb{R})$
for
$(a^t \tilde z^o_{a^t},\, t\in \mathbb{R})$
for
![]() $a>1$
was studied in more detail, and it was shown that this is a Bernoulli flow with infinite entropy.
$a>1$
was studied in more detail, and it was shown that this is a Bernoulli flow with infinite entropy.
4. Cell division processes
We consider a class of tessellation-valued Markov processes
![]() $(T_t,\, t>0)$
which are characterized by the laws of the random life times of the cells and the laws for the division of the cells by a random hyperplane at the end of their life times. Furthermore, given the state of the process, conditional independence of the future development in different cells is assumed.
$(T_t,\, t>0)$
which are characterized by the laws of the random life times of the cells and the laws for the division of the cells by a random hyperplane at the end of their life times. Furthermore, given the state of the process, conditional independence of the future development in different cells is assumed.
Definition 2. Let
![]() $\mathbb{Q} =(\mathbb{Q}_{[z]} ,\, z\in {\mathcal{P}_d} )$
, where
$\mathbb{Q} =(\mathbb{Q}_{[z]} ,\, z\in {\mathcal{P}_d} )$
, where
![]() $\mathbb{Q}_{[z]}$
is a probability measure on the set [z] of hyperplanes which intersect z, and let
$\mathbb{Q}_{[z]}$
is a probability measure on the set [z] of hyperplanes which intersect z, and let
![]() $G\colon{\mathcal{P}_d}\to[0,\infty)$
be a measurable functional defined on the set of polytopes.
$G\colon{\mathcal{P}_d}\to[0,\infty)$
be a measurable functional defined on the set of polytopes.
A random tessellation-valued process
![]() $(T_t,\, t>0)$
is called an (L-G) (D-
$(T_t,\, t>0)$
is called an (L-G) (D-
![]() $\mathbb{Q}$
) cell division process if, for all
$\mathbb{Q}$
) cell division process if, for all
![]() $t>0$
and all cells
$t>0$
and all cells
![]() $z\in T_t$
:
$z\in T_t$
:
-
(L-G) If
 $G(z)>0$
, then the cell z has a random life time which is exponentially distributed with parameter G(z) and, given z, conditionally independent of
$G(z)>0$
, then the cell z has a random life time which is exponentially distributed with parameter G(z) and, given z, conditionally independent of
 $(T_{t^{\prime}},\, 0<t^{\prime}<t)$
and of all other cells of
$(T_{t^{\prime}},\, 0<t^{\prime}<t)$
and of all other cells of
 $T_t$
. If
$T_t$
. If
 $G(z)=0$
then the life time is infinite, which means that z is never divided.
$G(z)=0$
then the life time is infinite, which means that z is never divided. -
(D-ℚ) At the end of its life time, z is divided by a random hyperplane
 $h_z$
with the law
$h_z$
with the law
 $\mathbb{Q}_{[z]}$
; also, given z, the hyperplane
$\mathbb{Q}_{[z]}$
; also, given z, the hyperplane
 $h_z$
is conditionally independent of
$h_z$
is conditionally independent of
 $(T_{t^{\prime}},\, 0<t^{\prime}<t)$
and of all other cells of
$(T_{t^{\prime}},\, 0<t^{\prime}<t)$
and of all other cells of
 $T_t$
, and independent of the life time of z.
$T_t$
, and independent of the life time of z.
It is not trivial to see whether such a cell division process
![]() $(T_t,\, t>0)$
exists for given G and
$(T_t,\, t>0)$
exists for given G and
![]() $\mathbb{Q}$
, because there is no appropriate initial tessellation at time
$\mathbb{Q}$
, because there is no appropriate initial tessellation at time
![]() $t=0$
. Even if it is clear how to perform the cell division dynamics in a bounded polytope W (a window), a consistent extension to the whole space
$t=0$
. Even if it is clear how to perform the cell division dynamics in a bounded polytope W (a window), a consistent extension to the whole space
![]() $\mathbb{R}^d$
is by no means straightforward.
$\mathbb{R}^d$
is by no means straightforward.
Examples of interest for such rules can be related to translation-invariant hyperplane measures
![]() $\Lambda$
which satisfy (1) and (2).
$\Lambda$
which satisfy (1) and (2).
We also have the following definitions:
-
(L-Λ) The life time of each cell z is exponentially distributed with parameter
 $\Lambda ([z])$
.
$\Lambda ([z])$
. -
(L-Vd) The life time of each cell z is exponentially distributed with parameter
 $V_d(z)$
, the volume of z.
$V_d(z)$
, the volume of z. -
(D-Λ) The law of the random hyperplane dividing a cell z is
 $\mathbb{Q}_{[z]} = \Lambda([z])^{-1}\Lambda(\cdot \cap [z])$
, which is the probability measure on [z] induced by
$\mathbb{Q}_{[z]} = \Lambda([z])^{-1}\Lambda(\cdot \cap [z])$
, which is the probability measure on [z] induced by
 $\Lambda$
.
$\Lambda$
.
The STIT tessellation process driven by
![]() $\Lambda$
is a cell division process with (L-
$\Lambda$
is a cell division process with (L-
![]() $\Lambda$
) and (D-
$\Lambda$
) and (D-
![]() $\Lambda$
). In [Reference Nagel and Biehler19] it was shown that in the class of cell division processes defined above, only the (L-
$\Lambda$
). In [Reference Nagel and Biehler19] it was shown that in the class of cell division processes defined above, only the (L-
![]() $\Lambda$
) (D-
$\Lambda$
) (D-
![]() $\Lambda$
) model has the property of spatial consistency which is sufficient for its existence. It is therefore of interest to show the existence of further cell division processes without requiring spatial consistency.
$\Lambda$
) model has the property of spatial consistency which is sufficient for its existence. It is therefore of interest to show the existence of further cell division processes without requiring spatial consistency.
4.1. A sufficient condition for the existence of a cell division process in
 $\mathbb{R}^d$
$\mathbb{R}^d$
Let
![]() $({\mathcal{P}_d} ,\mathcal{B} ({\mathcal{P}_d}))$
be the measurable space of d-dimensional polytopes, where
$({\mathcal{P}_d} ,\mathcal{B} ({\mathcal{P}_d}))$
be the measurable space of d-dimensional polytopes, where
![]() $\mathcal{B} ({\mathcal{P}_d})$
is the Borel
$\mathcal{B} ({\mathcal{P}_d})$
is the Borel
![]() $\sigma$
-algebra with respect to the Fell topology on the space of closed subsets of
$\sigma$
-algebra with respect to the Fell topology on the space of closed subsets of
![]() $\mathbb{R}^d$
[Reference Schneider and Weil25]. A functional
$\mathbb{R}^d$
[Reference Schneider and Weil25]. A functional
![]() $G\colon {\mathcal{P}_d} \to [0,\infty )$
is called monotone if
$G\colon {\mathcal{P}_d} \to [0,\infty )$
is called monotone if
![]() $G(z_1)\leq G(z_2)$
for all
$G(z_1)\leq G(z_2)$
for all
![]() $z_1,z_2 \in {\mathcal{P}_d}$
with
$z_1,z_2 \in {\mathcal{P}_d}$
with
![]() $z_1\subseteq z_2$
. It is called translation invariant if
$z_1\subseteq z_2$
. It is called translation invariant if
![]() $G(z)=G(z+x)$
for all
$G(z)=G(z+x)$
for all
![]() $z\in {\mathcal{P}_d}$
and all
$z\in {\mathcal{P}_d}$
and all
![]() $x\in \mathbb{R}^d$
.
$x\in \mathbb{R}^d$
.
Now we address the problem of under which assumptions on
![]() $\Lambda$
and G an (L-G) (D-
$\Lambda$
and G an (L-G) (D-
![]() $\Lambda$
) cell division process
$\Lambda$
) cell division process
![]() $(T_t,\, t>0)$
according to Definition 2 exists. If the whole space
$(T_t,\, t>0)$
according to Definition 2 exists. If the whole space
![]() $\mathbb{R}^d$
is considered, there is no initial tessellation at time
$\mathbb{R}^d$
is considered, there is no initial tessellation at time
![]() $t=0$
, and there is no time of ‘first division’. Therefore, an idea is to use an auxiliary process of zero-cells which is defined for all times
$t=0$
, and there is no time of ‘first division’. Therefore, an idea is to use an auxiliary process of zero-cells which is defined for all times
![]() $t>0$
and whose cells cover the whole
$t>0$
and whose cells cover the whole
![]() $\mathbb{R}^d$
as
$\mathbb{R}^d$
as
![]() $t\to 0$
. Then, for any time
$t\to 0$
. Then, for any time
![]() $t>0$
the future process inside the zero-cell at that time is constructed. The crucial issue is that these constructions launched at different times
$t>0$
the future process inside the zero-cell at that time is constructed. The crucial issue is that these constructions launched at different times
![]() $t_1 <t_2$
in different zero-cells must be compatible, in the sense that the distribution of the cell division process after
$t_1 <t_2$
in different zero-cells must be compatible, in the sense that the distribution of the cell division process after
![]() $t_2$
is identical for all
$t_2$
is identical for all
![]() $t_1\leq t_2$
. Intuitively, if such a construction is used, it is essential that the sum of the life times of the ‘ancestor’ cells of a zero-cell at time
$t_1\leq t_2$
. Intuitively, if such a construction is used, it is essential that the sum of the life times of the ‘ancestor’ cells of a zero-cell at time
![]() $t>0$
fits into the interval (0,1), i.e. the life times in the past are small enough. For a translation-invariant measure
$t>0$
fits into the interval (0,1), i.e. the life times in the past are small enough. For a translation-invariant measure
![]() $\Lambda$
a sufficient condition concerns the growth of the functional G. This is formalized in the following theorem.
$\Lambda$
a sufficient condition concerns the growth of the functional G. This is formalized in the following theorem.
Theorem 1.
Let
![]() $\Lambda$
be a translation-invariant measure on the space of hyperplanes in
$\Lambda$
be a translation-invariant measure on the space of hyperplanes in
![]() $\mathbb{R}^d$
, satisfying (1) and (2), and let
$\mathbb{R}^d$
, satisfying (1) and (2), and let
![]() $G\colon {\mathcal{P}_d} \to [0,\infty )$
be a measurable, monotone, and translation-invariant functional on the set of d-dimensional polytopes. If, for the random sequence
$G\colon {\mathcal{P}_d} \to [0,\infty )$
be a measurable, monotone, and translation-invariant functional on the set of d-dimensional polytopes. If, for the random sequence
![]() $(\tilde z^o_{(i)},\, i\in \mathbb{Z})$
defined in (4),
$(\tilde z^o_{(i)},\, i\in \mathbb{Z})$
defined in (4),
holds a.s., then there exists a Markov tessellation-valued process
![]() $(T_t,\, t>0)$
that is an (L-G) (D-
$(T_t,\, t>0)$
that is an (L-G) (D-
![]() $\Lambda$
) cell division process according to Definition 2.
$\Lambda$
) cell division process according to Definition 2.
Proof. The idea of the proof is inspired by the global construction of STIT tessellations described in [Reference Mecke, Nagel and Weiss18]. The key is a backward construction for
![]() $t\downarrow 0$
of the process
$t\downarrow 0$
of the process
![]() $(z^o_t,\, t>0)$
of zero-cells of
$(z^o_t,\, t>0)$
of zero-cells of
![]() $(T_t,\, t>0)$
.
$(T_t,\, t>0)$
.
The auxiliary process
![]() $(\hat X_t,\, t>0)$
of Poisson hyperplane tessellations has exactly the (D-
$(\hat X_t,\, t>0)$
of Poisson hyperplane tessellations has exactly the (D-
![]() $\Lambda$
) rule as the division law for its zero-cells. Hence, the sizes and shapes of the zero-cells of the Poisson hyperplane tessellations can be used for the construction of
$\Lambda$
) rule as the division law for its zero-cells. Hence, the sizes and shapes of the zero-cells of the Poisson hyperplane tessellations can be used for the construction of
![]() $(z^o_t,\, t>0)$
. What has to be changed is the ‘clock’. The time axis has to be transformed such that the pure jump process of zero-cells receives jump times according to (L-G), i.e. the life times of the respective cells are exponentially distributed, and the parameter is the functional value of G for these cells.
$(z^o_t,\, t>0)$
. What has to be changed is the ‘clock’. The time axis has to be transformed such that the pure jump process of zero-cells receives jump times according to (L-G), i.e. the life times of the respective cells are exponentially distributed, and the parameter is the functional value of G for these cells.
We use the random sequence
![]() $(\tilde z^o_{(i)},\, i\in \mathbb{Z})$
defined in (4) for the construction, and we assign appropriate holding times to it.
$(\tilde z^o_{(i)},\, i\in \mathbb{Z})$
defined in (4) for the construction, and we assign appropriate holding times to it.
Let
![]() $(\tau^{\prime}_i ,\, i\in \mathbb{Z})$
be a sequence of i.i.d. random variables, exponentially distributed with parameter 1; this sequence has to be independent of
$(\tau^{\prime}_i ,\, i\in \mathbb{Z})$
be a sequence of i.i.d. random variables, exponentially distributed with parameter 1; this sequence has to be independent of
![]() $\hat X^*$
. Define
$\hat X^*$
. Define
![]() $(\tau_i , \,i\in \mathbb{Z})$
as
$(\tau_i , \,i\in \mathbb{Z})$
as
By (7) there is a.s. an
![]() $i\in \mathbb{Z}$
such that
$i\in \mathbb{Z}$
such that
![]() $\tau_i$
is finite if and only if (8) holds a.s. Hence, (8) is sufficient for the existence of the process
$\tau_i$
is finite if and only if (8) holds a.s. Hence, (8) is sufficient for the existence of the process
![]() $(z^o_t,\, t>0)$
which is defined by
$(z^o_t,\, t>0)$
which is defined by
And this also implies that
![]() $\lim_{j\to -\infty} \tau_j = 0$
a.s., and hence
$\lim_{j\to -\infty} \tau_j = 0$
a.s., and hence
![]() $\bigcup_{t>0} z^o_t = \mathbb{R}^d$
by (3).
$\bigcup_{t>0} z^o_t = \mathbb{R}^d$
by (3).
Having shown the existence of the process
![]() $(z^o_t,\, t>0)$
of zero-cells, the process
$(z^o_t,\, t>0)$
of zero-cells, the process
![]() $(T_t,\, t>0)$
is completed as follows. Denote by
$(T_t,\, t>0)$
is completed as follows. Denote by
![]() $\text{cl}$
the topological closure of a subset of
$\text{cl}$
the topological closure of a subset of
![]() $\mathbb{R}^d$
. At each time
$\mathbb{R}^d$
. At each time
![]() $\tau_i$
, when the process
$\tau_i$
, when the process
![]() $(z^o_t,\, t>0)$
has a jump from
$(z^o_t,\, t>0)$
has a jump from
![]() $\tilde z^o_{(i-1)}$
to
$\tilde z^o_{(i-1)}$
to
![]() $\tilde z^o_{(i)}$
, an (L-G) (D-
$\tilde z^o_{(i)}$
, an (L-G) (D-
![]() $\Lambda$
) cell division process according to Definition 2 is launched in the new separated cell
$\Lambda$
) cell division process according to Definition 2 is launched in the new separated cell
![]() $\text{cl}\big(\tilde z^o_{(i-1)} \setminus \tilde z^o_{(i)}\big)$
.
$\text{cl}\big(\tilde z^o_{(i-1)} \setminus \tilde z^o_{(i)}\big)$
.
It remains to show that this actually yields a tessellation
![]() $T_t$
for all
$T_t$
for all
![]() $t>0$
, and that the process
$t>0$
, and that the process
![]() $(T_t,\, t>0)$
is an (L-G) (D-
$(T_t,\, t>0)$
is an (L-G) (D-
![]() $\Lambda$
) cell division process.
$\Lambda$
) cell division process.
Condition (ii) of Definition 1 is obviously satisfied. To show (i), consider an arbitrary point
![]() $x\in \mathbb{R}^d$
. Then (3) implies that
$x\in \mathbb{R}^d$
. Then (3) implies that
![]() $x\in z^o_s$
for
$x\in z^o_s$
for
![]() $0<s<t_x$
, where
$0<s<t_x$
, where
![]() $t_x$
is the time when x and o are separated by a hyperplane. Thus, the construction guarantees that, for all
$t_x$
is the time when x and o are separated by a hyperplane. Thus, the construction guarantees that, for all
![]() $t>0$
, any point
$t>0$
, any point
![]() $x\in \mathbb{R}^d$
belongs to the interior or to the boundary of a cell of
$x\in \mathbb{R}^d$
belongs to the interior or to the boundary of a cell of
![]() $T_t$
.
$T_t$
.
To prove property (iii) of Definition 1, consider a compact set
![]() $C\subset \mathbb{R}^d$
and a time
$C\subset \mathbb{R}^d$
and a time
![]() $t_0 > 0$
such that
$t_0 > 0$
such that
![]() $C\subset z^o_{t_0}$
. By (3), such a time exists. Thus, for all
$C\subset z^o_{t_0}$
. By (3), such a time exists. Thus, for all
![]() $t\leq t_0$
, there is exactly one cell in
$t\leq t_0$
, there is exactly one cell in
![]() $T_t$
that has a nonempty intersection with C. For
$T_t$
that has a nonempty intersection with C. For
![]() $t>t_0$
the number of cells inside
$t>t_0$
the number of cells inside
![]() $z^o_{t_0}$
of the cell division process can be described by a birth process. By the monotonicity and translation invariance of G, the birth rates are dominated by
$z^o_{t_0}$
of the cell division process can be described by a birth process. By the monotonicity and translation invariance of G, the birth rates are dominated by
![]() $G(z^o_{t_0})\times \, \textit{number of cells in}\ G(z^o_{t_0})$
. Hence, at any time
$G(z^o_{t_0})\times \, \textit{number of cells in}\ G(z^o_{t_0})$
. Hence, at any time
![]() $t>0$
, the number of cells intersecting C is a.s. finite.
$t>0$
, the number of cells intersecting C is a.s. finite.
Finally, to see that the process
![]() $(T_t,\, t>0)$
is an (L-G) (D-
$(T_t,\, t>0)$
is an (L-G) (D-
![]() $\Lambda$
) cell division process, observe that the division rule for the zero-cell process is induced by the Poisson hyperplane process
$\Lambda$
) cell division process, observe that the division rule for the zero-cell process is induced by the Poisson hyperplane process
![]() $\hat X$
and thus the (D-
$\hat X$
and thus the (D-
![]() $\Lambda$
) rule is realized. The definition in (10) yields that the holding time of the state
$\Lambda$
) rule is realized. The definition in (10) yields that the holding time of the state
![]() $z^o_{(i)}$
is
$z^o_{(i)}$
is
![]() $\tau_{i+1} - \tau_i = G\big(\tilde z^o_{(i)}\big)^{-1}\tau^{\prime}_i$
, which shows that (L-G) is satisfied for the zero-cell process. For cells which are already separated from the zero-cell, the (L-G) and (D-
$\tau_{i+1} - \tau_i = G\big(\tilde z^o_{(i)}\big)^{-1}\tau^{\prime}_i$
, which shows that (L-G) is satisfied for the zero-cell process. For cells which are already separated from the zero-cell, the (L-G) and (D-
![]() $\Lambda$
) rules are satisfied by the definition of the construction.
$\Lambda$
) rules are satisfied by the definition of the construction.
In the rest of this paper, we always mean by an (L-G) (D-
![]() $\Lambda$
) process
$\Lambda$
) process
![]() $(T_t,\, t>0)$
the tessellation-valued process defined in the proof. Note that the proof does not imply that the distribution of the (L-G) (D-
$(T_t,\, t>0)$
the tessellation-valued process defined in the proof. Note that the proof does not imply that the distribution of the (L-G) (D-
![]() $\Lambda$
) process is uniquely determined by G and
$\Lambda$
) process is uniquely determined by G and
![]() $\Lambda$
.
$\Lambda$
.
An example where the sufficient condition (8) is obviously not satisfied is
![]() $G(z)=c$
for all
$G(z)=c$
for all
![]() $z\in {\mathcal{P}_d}$
and some fixed
$z\in {\mathcal{P}_d}$
and some fixed
![]() $c>0$
. It is not known whether a cell division tessellation process exists for this G, but the simulations in [Reference Cowan3] for the corresponding ‘equally likely’ case suggest that the cell division does not yield a tessellation according to Definition 1, because the local finiteness condition (iii) seems to be violated.
$c>0$
. It is not known whether a cell division tessellation process exists for this G, but the simulations in [Reference Cowan3] for the corresponding ‘equally likely’ case suggest that the cell division does not yield a tessellation according to Definition 1, because the local finiteness condition (iii) seems to be violated.
4.2. Stationarity in space
Now we show that the translation invariance of the hyperplane measure
![]() $\Lambda$
and of the functional G are sufficient for the spatial stationarity of the constructed tessellations at any fixed time
$\Lambda$
and of the functional G are sufficient for the spatial stationarity of the constructed tessellations at any fixed time
![]() $t>0$
.
$t>0$
.
Theorem 2.
If the assumptions of Theorem 1 are satisfied then, for all
![]() $t>0$
, the random tessellation
$t>0$
, the random tessellation
![]() $T_t$
described in the proof of the theorem is a spatially stationary (or homogeneous) tessellation.
$T_t$
described in the proof of the theorem is a spatially stationary (or homogeneous) tessellation.
Proof. The proof can be sketched as follows. Because the hyperplane measure
![]() $\Lambda$
defined in (1) is invariant under translations of
$\Lambda$
defined in (1) is invariant under translations of
![]() $\mathbb{R}^d$
, the distribution of the auxiliary Poisson process
$\mathbb{R}^d$
, the distribution of the auxiliary Poisson process
![]() $\hat X^*$
is invariant under translations by
$\hat X^*$
is invariant under translations by
![]() $(x,0)\in \mathbb{R}^d \times \{ 0\}$
. Thus, denoting by
$(x,0)\in \mathbb{R}^d \times \{ 0\}$
. Thus, denoting by
![]() $\big(\tilde z^o_{(i)}(\hat X^* ),\, i\in \mathbb{Z}\big)$
the process of zero-cells generated by
$\big(\tilde z^o_{(i)}(\hat X^* ),\, i\in \mathbb{Z}\big)$
the process of zero-cells generated by
![]() $\hat X^*$
,
$\hat X^*$
,
This means invariance under translations of
![]() $\mathbb{R}^d$
for the distribution of the process
$\mathbb{R}^d$
for the distribution of the process
![]() $(\tilde z^o_{(i)},\, i\in \mathbb{Z})$
defined in (4).
$(\tilde z^o_{(i)},\, i\in \mathbb{Z})$
defined in (4).
Furthermore, the translation invariance of G guarantees that the life time distributions of the cells remain translation invariant too. Finally, because
![]() $\Lambda$
is invariant under translations, it follows that
$\Lambda$
is invariant under translations, it follows that
![]() $\Lambda([z+x])^{-1}\Lambda(A+x\cap[z+x]) = \Lambda([z])^{-1}\Lambda(A \cap [z])$
for all
$\Lambda([z+x])^{-1}\Lambda(A+x\cap[z+x]) = \Lambda([z])^{-1}\Lambda(A \cap [z])$
for all
![]() $z\in {\mathcal{P}_d}$
,
$z\in {\mathcal{P}_d}$
,
![]() $x\in \mathbb{R}^d$
, and Borel sets
$x\in \mathbb{R}^d$
, and Borel sets
![]() $A\subset [z]$
. Hence, the division law is translation equivariant.
$A\subset [z]$
. Hence, the division law is translation equivariant.
4.3. Construction of the cut-out appearing in a bounded window W
For simulations of the model it is of interest to construct the restriction
![]() $(T_t \land W,\, t>0)$
of
$(T_t \land W,\, t>0)$
of
![]() $(T_t,\, t>0)$
to a bounded window
$(T_t,\, t>0)$
to a bounded window
![]() $W\in {\mathcal{P}_d}$
, where
$W\in {\mathcal{P}_d}$
, where
![]() $T_t \land W :\!= \{ z\cap W \colon z\in T_t,\, \text{int}(z\cap W)\not= \emptyset\}$
. It was shown in [Reference Nagel and Weiß21] that, for STIT tessellations, the (L-
$T_t \land W :\!= \{ z\cap W \colon z\in T_t,\, \text{int}(z\cap W)\not= \emptyset\}$
. It was shown in [Reference Nagel and Weiß21] that, for STIT tessellations, the (L-
![]() $\Lambda$
) (D-
$\Lambda$
) (D-
![]() $\Lambda$
) cell division process can be launched in W without regarding boundary effects, because the STIT model is spatially consistent. And in [Reference Nagel and Biehler19] it was shown that all the other models considered in the present paper are not spatially consistent, which means that for the construction of
$\Lambda$
) cell division process can be launched in W without regarding boundary effects, because the STIT model is spatially consistent. And in [Reference Nagel and Biehler19] it was shown that all the other models considered in the present paper are not spatially consistent, which means that for the construction of
![]() $(T_t \land W,\, t>0)$
information outside of W is also needed.
$(T_t \land W,\, t>0)$
information outside of W is also needed.
The construction described in the proof of Theorem 1 also shows how
![]() $(T_t \land W,\, t>0)$
can be realized. For a given window W construct a zero-cell
$(T_t \land W,\, t>0)$
can be realized. For a given window W construct a zero-cell
![]() $\tilde z^o_{(i_W)}$
from the process
$\tilde z^o_{(i_W)}$
from the process
![]() $(\tilde z^o_{(i)},\, i\in \mathbb{Z})$
defined in (4) such that
$(\tilde z^o_{(i)},\, i\in \mathbb{Z})$
defined in (4) such that
![]() $ W \subset \tilde z^o_{(i_W)}$
. This can be done as follows. Let
$ W \subset \tilde z^o_{(i_W)}$
. This can be done as follows. Let
![]() $R>0$
be such that
$R>0$
be such that
![]() $W\subset {\sf B}_R$
. Simulate the restricted Poisson point process
$W\subset {\sf B}_R$
. Simulate the restricted Poisson point process
![]() $\hat X^* \cap ([ {\sf B}_{nR}] \times (0, {1}/{n}))$
, starting with
$\hat X^* \cap ([ {\sf B}_{nR}] \times (0, {1}/{n}))$
, starting with
![]() $n=2$
. If the generated zero-cell contains W, then choose it as
$n=2$
. If the generated zero-cell contains W, then choose it as
![]() $\tilde z^o_{(i_W)}$
; otherwise update
$\tilde z^o_{(i_W)}$
; otherwise update
![]() $n:\!=n+1$
until an appropriate zero-cell is simulated.
$n:\!=n+1$
until an appropriate zero-cell is simulated.
Then launch the (L-G) (D-
![]() $\Lambda$
) cell division process inside
$\Lambda$
) cell division process inside
![]() $\tilde z^o_{(i_W)}$
. Its restriction to W has exactly the distribution of
$\tilde z^o_{(i_W)}$
. Its restriction to W has exactly the distribution of
![]() $(T_{t+\tau_{i_W}} \land W,\, t>0)$
. Here, the jump time
$(T_{t+\tau_{i_W}} \land W,\, t>0)$
. Here, the jump time
![]() $\tau_{i_W}$
of the zero-cell process is unknown because we do not know the value of the series in (9).
$\tau_{i_W}$
of the zero-cell process is unknown because we do not know the value of the series in (9).
5. The Mondrian directional distribution
Now we study a particular class of directional distributions
![]() $\varphi$
and functionals G where the sufficient condition of Theorem 1 is satisfied.
$\varphi$
and functionals G where the sufficient condition of Theorem 1 is satisfied.
Denote by
![]() $e_1,\ldots , e_d$
the orthonormal base of
$e_1,\ldots , e_d$
the orthonormal base of
![]() $\mathbb{R}^d$
with
$\mathbb{R}^d$
with
![]() $e_k :\!= (0, \ldots ,0, 1,0\ldots 0)$
where the 1 is at the kth position,
$e_k :\!= (0, \ldots ,0, 1,0\ldots 0)$
where the 1 is at the kth position,
![]() $k\in \{1,\ldots , d\}$
. Let
$k\in \{1,\ldots , d\}$
. Let
![]() $\delta_{e_k}$
denote the Dirac probability measure defined on
$\delta_{e_k}$
denote the Dirac probability measure defined on
![]() $S^{d-1}$
and with mass 1 on
$S^{d-1}$
and with mass 1 on
![]() $e_k$
.
$e_k$
.
In this section we consider spherical directional distributions of the form
 \begin{equation} \varphi = \frac{1}{2} \sum_{k=1}^d p_k (\delta_{e_k}+\delta_{-e_k}) ,\qquad p_k >0, \ \sum_{k=1}^d p_k =1.\end{equation}
\begin{equation} \varphi = \frac{1}{2} \sum_{k=1}^d p_k (\delta_{e_k}+\delta_{-e_k}) ,\qquad p_k >0, \ \sum_{k=1}^d p_k =1.\end{equation}
Referring to recent papers like [Reference O’Reilly and Tran24], we will call them Mondrian directional distributions.
The random tessellations generated by Mondrian directional distributions consist of cuboids (orthogonal parallelepipeds). As mentioned above, the volume
![]() $G=V_d$
is a functional of interest for the life time distribution, and so are the other intrinsic volumes
$G=V_d$
is a functional of interest for the life time distribution, and so are the other intrinsic volumes
![]() $G=V_n$
,
$G=V_n$
,
![]() $n\in \{ 1,\ldots ,d-1\}$
, including the surface content and the mean width of a cell. For cuboids these intrinsic volumes depend on the side lengths only, see (15). Thus, the sufficient condition of Theorem 1 can be checked by proving that these side lengths are ‘long enough’. See Figure 1 for an example.
$n\in \{ 1,\ldots ,d-1\}$
, including the surface content and the mean width of a cell. For cuboids these intrinsic volumes depend on the side lengths only, see (15). Thus, the sufficient condition of Theorem 1 can be checked by proving that these side lengths are ‘long enough’. See Figure 1 for an example.

Figure 1. Simulations of cell division tessellations in a quadratic window with (L-
![]() $\Lambda$
) (left panel) and (L-
$\Lambda$
) (left panel) and (L-
![]() $V_2$
) (right panel), both with (D-
$V_2$
) (right panel), both with (D-
![]() $\Lambda$
). The directional distribution is
$\Lambda$
). The directional distribution is
![]() $\varphi = \frac{1}{2} \delta_{e_1} + \frac{1}{2} \delta_{e_2}$
. (Generated with the software from [Reference León10].)
$\varphi = \frac{1}{2} \delta_{e_1} + \frac{1}{2} \delta_{e_2}$
. (Generated with the software from [Reference León10].)
Theorems 3 and 4 provide the first concrete models of cell-division processes in
![]() $\mathbb{R}^d$
that differ from the STIT model.
$\mathbb{R}^d$
that differ from the STIT model.
5.1. Existence results
For a d-dimensional cuboid z with all
![]() $(d-1)$
-dimensional faces parallel or orthogonal to the axes in
$(d-1)$
-dimensional faces parallel or orthogonal to the axes in
![]() $\mathbb{R}^d$
, denote by
$\mathbb{R}^d$
, denote by
![]() $l^{(1)},\ldots ,l^{(d)}$
the side lengths of the cuboid, where
$l^{(1)},\ldots ,l^{(d)}$
the side lengths of the cuboid, where
![]() $l^{(k)}$
is the length of the sides that are parallel to
$l^{(k)}$
is the length of the sides that are parallel to
![]() $e_k$
,
$e_k$
,
![]() $k\in \{ 1,\ldots , d\}$
. Write
$k\in \{ 1,\ldots , d\}$
. Write
![]() $S(z):\!= \sum_{k=1}^d l^{(k)}$
if z is a cuboid and
$S(z):\!= \sum_{k=1}^d l^{(k)}$
if z is a cuboid and
![]() $S(z)=1$
elsewhere.
$S(z)=1$
elsewhere.
Theorem 3.
Let
![]() $\Lambda$
be a translation-invariant measure on the space of hyperplanes in
$\Lambda$
be a translation-invariant measure on the space of hyperplanes in
![]() $\mathbb{R}^d$
satisfying (1), where
$\mathbb{R}^d$
satisfying (1), where
![]() $\varphi$
is a Mondrian directional distribution (11). Then there exists a Markov tessellation-valued process
$\varphi$
is a Mondrian directional distribution (11). Then there exists a Markov tessellation-valued process
![]() $(T_t,\, t>0)$
that is an (L-S) (D-
$(T_t,\, t>0)$
that is an (L-S) (D-
![]() $\Lambda$
) cell division process according to Definition 2.
$\Lambda$
) cell division process according to Definition 2.
Proof. Consider the auxiliary Poisson process
![]() $\hat X^*$
of hyperplanes that are marked with birth times, i.e. the Poisson point process on
$\hat X^*$
of hyperplanes that are marked with birth times, i.e. the Poisson point process on
![]() $\mathcal{H} \times (0,\infty )$
with the intensity measure
$\mathcal{H} \times (0,\infty )$
with the intensity measure
![]() $\Lambda \otimes \lambda_+$
, see Section 2, and
$\Lambda \otimes \lambda_+$
, see Section 2, and
![]() $\Lambda$
defined in (1) with
$\Lambda$
defined in (1) with
![]() $\varphi$
as in (11). We show that the sufficient condition of Theorem 1 is satisfied for the functional
$\varphi$
as in (11). We show that the sufficient condition of Theorem 1 is satisfied for the functional
![]() $G=S$
, which is monotone and translation invariant on the class of cuboids.
$G=S$
, which is monotone and translation invariant on the class of cuboids.
The Poisson point process
![]() $\hat X^*$
can be described as a superposition of d i.i.d. Poisson point processes
$\hat X^*$
can be described as a superposition of d i.i.d. Poisson point processes
![]() $\hat X^{(k)*}$
, i.e.
$\hat X^{(k)*}$
, i.e.
![]() $\hat X^*\stackrel{\textrm{D}}{=}\bigcup_{k=1}^d \hat X^{(k)*}$
where
$\hat X^*\stackrel{\textrm{D}}{=}\bigcup_{k=1}^d \hat X^{(k)*}$
where
![]() $\hat X^{(k)*}$
is a Poisson point process on
$\hat X^{(k)*}$
is a Poisson point process on
![]() $\mathcal{H} \times (0,\infty)$
with the intensity measure
$\mathcal{H} \times (0,\infty)$
with the intensity measure
![]() $p_k \Lambda^{(k)} \otimes \lambda_+$
, and
$p_k \Lambda^{(k)} \otimes \lambda_+$
, and
![]() $\Lambda^{(k)}$
is as defined in (1) with
$\Lambda^{(k)}$
is as defined in (1) with
![]() $\varphi^{(k)} =\frac{1}{2}(\delta_{e_k}+ \delta_{-e_k})$
,
$\varphi^{(k)} =\frac{1}{2}(\delta_{e_k}+ \delta_{-e_k})$
,
![]() $k\in \{ 1,\ldots , d\}$
(for which condition (2) is obviously not satisfied).
$k\in \{ 1,\ldots , d\}$
(for which condition (2) is obviously not satisfied).
For
![]() $k\in \{ 1,\ldots , d\} $
we define the Poisson point processes
$k\in \{ 1,\ldots , d\} $
we define the Poisson point processes
![]() $\Phi^{k+}$
and
$\Phi^{k+}$
and
![]() $\Phi^{k-}$
on
$\Phi^{k-}$
on
![]() $(0,\infty )\times (0,\infty )$
as the birth-time-marked processes of intersection points of the hyperplanes of
$(0,\infty )\times (0,\infty )$
as the birth-time-marked processes of intersection points of the hyperplanes of
![]() $\hat X^{(k)*}$
with the positive axis and the negative axis in direction
$\hat X^{(k)*}$
with the positive axis and the negative axis in direction
![]() $e_k$
and
$e_k$
and
![]() $-e_k$
, respectively. Formally,
$-e_k$
, respectively. Formally,
 \begin{align*} \Phi^{k+} & :\!= \big\{(x,t)\in(0,\infty)\times(0,\infty)\colon(h(e_k,x),t)\in\hat X^{(k)*}\big\}, \\ \Phi^{k-} & :\!= \big\{(x,t)\in(0,\infty)\times(0,\infty)\colon(h(\!{-}e_k,x),t)\in\hat X^{(k)*}\big\}. \end{align*}
\begin{align*} \Phi^{k+} & :\!= \big\{(x,t)\in(0,\infty)\times(0,\infty)\colon(h(e_k,x),t)\in\hat X^{(k)*}\big\}, \\ \Phi^{k-} & :\!= \big\{(x,t)\in(0,\infty)\times(0,\infty)\colon(h(\!{-}e_k,x),t)\in\hat X^{(k)*}\big\}. \end{align*}
Both point processes have the intensity measure
![]() $p_k \lambda_+ \otimes \lambda_+$
. Now we define the Markov chains
$p_k \lambda_+ \otimes \lambda_+$
. Now we define the Markov chains
![]() $M^{k+}=((x^{k+}_n,t^{k+}_n),\,n\in\mathbb{N}_0)$
with
$M^{k+}=((x^{k+}_n,t^{k+}_n),\,n\in\mathbb{N}_0)$
with
![]() $(x^{k+}_n,t^{k+}_n)\in \Phi^{k+}$
and
$(x^{k+}_n,t^{k+}_n)\in \Phi^{k+}$
and
![]() $x^{k+}_0:\!=\min\{x\colon(x,t)\in\Phi^{k+},t\leq 1\}$
,
$x^{k+}_0:\!=\min\{x\colon(x,t)\in\Phi^{k+},t\leq 1\}$
,
![]() $x^{k+}_{n+1}:\!=\min\{x\colon(x,t)\in\Phi^{k+},t\leq t^{k+}_n\}$
,
$x^{k+}_{n+1}:\!=\min\{x\colon(x,t)\in\Phi^{k+},t\leq t^{k+}_n\}$
,
![]() $n\in \mathbb{N}_0$
.
$n\in \mathbb{N}_0$
.
The times
![]() $t^{k+}_n$
are a.s. uniquely defined by the condition
$t^{k+}_n$
are a.s. uniquely defined by the condition
![]() $(x^{k+}_n,t^{k+}_n)\in \Phi^{k+}$
. Correspondingly,
$(x^{k+}_n,t^{k+}_n)\in \Phi^{k+}$
. Correspondingly,
![]() $M^{k-}$
is defined by replacing
$M^{k-}$
is defined by replacing
![]() $k+$
by
$k+$
by
![]() $k-$
.
$k-$
.
The properties of the Poisson process
![]() $\hat X^*$
yield that, for fixed
$\hat X^*$
yield that, for fixed
![]() $k\in\{1,\ldots,d\}$
, the Markov chains
$k\in\{1,\ldots,d\}$
, the Markov chains
![]() $M^{k+}$
and
$M^{k+}$
and
![]() $M^{k-}$
are i.i.d.
$M^{k-}$
are i.i.d.
Let us consider some properties of
![]() $M^{k+}$
. The random variable
$M^{k+}$
. The random variable
![]() $x^{k+}_0$
is exponentially distributed with parameter
$x^{k+}_0$
is exponentially distributed with parameter
![]() $p_k$
, and
$p_k$
, and
![]() $t^{k+}_0$
is uniformly distributed in the interval (0,1). Then,
$t^{k+}_0$
is uniformly distributed in the interval (0,1). Then,
![]() $x^{k+}_{n+1}-x^{k+}_n$
is exponentially distributed with the parameter
$x^{k+}_{n+1}-x^{k+}_n$
is exponentially distributed with the parameter
![]() $p_k t^{k+}_n$
and is independent of
$p_k t^{k+}_n$
and is independent of
![]() $x^{k+}_0,\ldots , x^{k+}_n$
and, given
$x^{k+}_0,\ldots , x^{k+}_n$
and, given
![]() $t^{k+}_n$
, conditionally independent of
$t^{k+}_n$
, conditionally independent of
![]() $t^{k+}_0,\ldots , t^{k+}_{n-1}$
. Furthermore,
$t^{k+}_0,\ldots , t^{k+}_{n-1}$
. Furthermore,
![]() $t^{k+}_{n+1}$
is uniformly distributed in the interval
$t^{k+}_{n+1}$
is uniformly distributed in the interval
![]() $(0,t^{k+}_n)$
and, given
$(0,t^{k+}_n)$
and, given
![]() $t^{k+}_n$
, conditionally independent of
$t^{k+}_n$
, conditionally independent of
![]() $x^{k+}_0,\ldots , x^{k+}_n$
and of
$x^{k+}_0,\ldots , x^{k+}_n$
and of
![]() $t^{k+}_0,\ldots , t^{k+}_{n-1}$
.
$t^{k+}_0,\ldots , t^{k+}_{n-1}$
.
Now consider the Markov chain
![]() $((S_{i},t_{i}),\, i \in \mathbb{Z}_-)$
, where
$((S_{i},t_{i}),\, i \in \mathbb{Z}_-)$
, where
![]() $(t_i,\,i\in\mathbb{Z})$
is the ordered sequence of jump times of
$(t_i,\,i\in\mathbb{Z})$
is the ordered sequence of jump times of
![]() $(\tilde z^o_t,\, t>0)$
with
$(\tilde z^o_t,\, t>0)$
with
![]() $t_0<1<t_1$
, as defined in Section 2, and
$t_0<1<t_1$
, as defined in Section 2, and
![]() $S_i:\!= S(\tilde z^o_{(i)})$
. Thus we have
$S_i:\!= S(\tilde z^o_{(i)})$
. Thus we have
![]() $t_0 = \max \{ t^{k+}_0, t^{k-}_0 , k\in \{ 1,\ldots , d\} \}$
, and
$t_0 = \max \{ t^{k+}_0, t^{k-}_0 , k\in \{ 1,\ldots , d\} \}$
, and
![]() $S_0= \sum_{k=1}^d x^{k+}_0 + x^{k-}_0 $
. By recursion,
$S_0= \sum_{k=1}^d x^{k+}_0 + x^{k-}_0 $
. By recursion,
![]() $t_{i-1}=\max\{t^{k+}_n<t_i,t^{k-}_n<t_i,\,k\in\{1,\ldots,d\},\,n\in\mathbb{Z}_-\}$
, and
$t_{i-1}=\max\{t^{k+}_n<t_i,t^{k-}_n<t_i,\,k\in\{1,\ldots,d\},\,n\in\mathbb{Z}_-\}$
, and
 \begin{equation} S_{i-1} = \begin{cases} S_i + x^{k+}_{m+1}-x^{k+}_m & \text{ if } t_{i} =t^{k+}_m \text{ for some } m\in \mathbb{Z}_- , \\ S_i + x^{k-}_{m+1}-x^{k-}_m & \text{ if } t_i = t^{k-}_m \text{ for some } m\in \mathbb{Z}_- . \end{cases}\end{equation}
\begin{equation} S_{i-1} = \begin{cases} S_i + x^{k+}_{m+1}-x^{k+}_m & \text{ if } t_{i} =t^{k+}_m \text{ for some } m\in \mathbb{Z}_- , \\ S_i + x^{k-}_{m+1}-x^{k-}_m & \text{ if } t_i = t^{k-}_m \text{ for some } m\in \mathbb{Z}_- . \end{cases}\end{equation}
Let
![]() $(R_i, \, i\in \mathbb{Z} )$
be a sequence of i.i.d. random variables with the probability density
$(R_i, \, i\in \mathbb{Z} )$
be a sequence of i.i.d. random variables with the probability density
![]() $f(r)= 2d r^{2d-1} \textbf{1}\{ 0<r<1 \}$
, i.e.
$f(r)= 2d r^{2d-1} \textbf{1}\{ 0<r<1 \}$
, i.e.
![]() $R_i$
has the distribution of the maximum of 2d i.i.d. random variables that are uniformly distributed in the interval (0,1).
$R_i$
has the distribution of the maximum of 2d i.i.d. random variables that are uniformly distributed in the interval (0,1).
Thus, the law of the time component
![]() $t_i$
in the Markov chain
$t_i$
in the Markov chain
![]() $((S_{i},t_{i}),\,i\in\mathbb{Z}_-)$
can be described by
$((S_{i},t_{i}),\,i\in\mathbb{Z}_-)$
can be described by
![]() $t_0 \stackrel{\textrm{D}}{=} R_0$
, and, by recursion,
$t_0 \stackrel{\textrm{D}}{=} R_0$
, and, by recursion,
![]() $t_{i-1}\stackrel{\textrm{D}}{=}t_i\,R_{i-1}$
,
$t_{i-1}\stackrel{\textrm{D}}{=}t_i\,R_{i-1}$
,
![]() $i \in \mathbb{Z}_-$
. Thus,
$i \in \mathbb{Z}_-$
. Thus,
The law of
![]() $S_{i-1}-S_i$
depends on both
$S_{i-1}-S_i$
depends on both
![]() $t_{i}$
and the index
$t_{i}$
and the index
![]() $k^+$
or
$k^+$
or
![]() $k^-$
. It is the exponential distribution with parameter
$k^-$
. It is the exponential distribution with parameter
![]() $p_k t_{i}$
, not depending on the sign of the index k.
$p_k t_{i}$
, not depending on the sign of the index k.
Let
![]() $(\kappa_i ,\, i\in \mathbb{Z} )$
be a sequence of i.i.d. random variables, exponentially distributed with parameter 1. This sequence is assumed to be independent of all the other random variables we have considered so far. Then the conditional distribution is
$(\kappa_i ,\, i\in \mathbb{Z} )$
be a sequence of i.i.d. random variables, exponentially distributed with parameter 1. This sequence is assumed to be independent of all the other random variables we have considered so far. Then the conditional distribution is
under the condition that
![]() $t_i =t^{k+}_m$
or
$t_i =t^{k+}_m$
or
![]() $t_i =t^{k-}_m$
for some
$t_i =t^{k-}_m$
for some
![]() $m \in \mathbb{N}_0$
, with
$m \in \mathbb{N}_0$
, with
![]() $p_{\min} :\!= \min \{ p_1,\ldots , p_k\}$
.
$p_{\min} :\!= \min \{ p_1,\ldots , p_k\}$
.
Thus, a sufficient condition for
is
Note that in (14) the item
![]() $S_0^{-1} $
is neglected in order to simplify the technicalities. To verify (14) we provide an upper bound for the expectation of the random variable on the left-hand side:
$S_0^{-1} $
is neglected in order to simplify the technicalities. To verify (14) we provide an upper bound for the expectation of the random variable on the left-hand side:
 \begin{align*} \mathbb{E}\textstyle\sum_{i\leq 0} \big(\textstyle\sum_{\ell=i}^0\big(\textstyle\prod_{j=\ell}^0 R_j\big)^{-1}\kappa_\ell\big)^{-1} & \leq \mathbb{E}\textstyle\sum_{i\leq 0} \big(\textstyle\sum_{\ell=i}^{i+1}\big(\textstyle\prod_{j=\ell}^0 R_j\big)^{-1}\kappa_\ell\big)^{-1} \\ & = \mathbb{E}\sum_{i\leq 0}\frac{\prod_{j=i+1}^{0} R_j}{ R_i^{-1} \, \kappa_i +\kappa_{i+1}} \\ & \leq \mathbb{E}\sum_{i\leq 0}\frac{\prod_{j=i+1}^{0} R_j}{ \kappa_i + \kappa_{i+1}} \\ & = \mathbb{E}\frac{1}{\kappa_0 + \kappa_{1}}\sum_{i\leq 0}\Bigg(\prod_{j=i+1}^{0}\mathbb{E}R_j\Bigg) \\ & = \sum_{i\leq 0}\Bigg(\prod_{j=i+1}^{0}\frac{2d}{2d+1}\Bigg) < \infty . \end{align*}
\begin{align*} \mathbb{E}\textstyle\sum_{i\leq 0} \big(\textstyle\sum_{\ell=i}^0\big(\textstyle\prod_{j=\ell}^0 R_j\big)^{-1}\kappa_\ell\big)^{-1} & \leq \mathbb{E}\textstyle\sum_{i\leq 0} \big(\textstyle\sum_{\ell=i}^{i+1}\big(\textstyle\prod_{j=\ell}^0 R_j\big)^{-1}\kappa_\ell\big)^{-1} \\ & = \mathbb{E}\sum_{i\leq 0}\frac{\prod_{j=i+1}^{0} R_j}{ R_i^{-1} \, \kappa_i +\kappa_{i+1}} \\ & \leq \mathbb{E}\sum_{i\leq 0}\frac{\prod_{j=i+1}^{0} R_j}{ \kappa_i + \kappa_{i+1}} \\ & = \mathbb{E}\frac{1}{\kappa_0 + \kappa_{1}}\sum_{i\leq 0}\Bigg(\prod_{j=i+1}^{0}\mathbb{E}R_j\Bigg) \\ & = \sum_{i\leq 0}\Bigg(\prod_{j=i+1}^{0}\frac{2d}{2d+1}\Bigg) < \infty . \end{align*}
In the last equation we used that the sum of two i.i.d. exponentially distributed random variables with parameter 1 has a gamma distribution with parameter (2,1), also referred to as an Erlang distribution, and hence
![]() $\mathbb{E}(\kappa_0 + \kappa_{1})^{-1}=1$
. We have thus shown that (14) is satisfied.
$\mathbb{E}(\kappa_0 + \kappa_{1})^{-1}=1$
. We have thus shown that (14) is satisfied.
In order to generalize the result for Mondrian directional distributions, we consider the individual side lengths of the zero-cells. Denote by
![]() $l_i^{(1)},\ldots ,l_i^{(d)} $
the side lengths of the cuboid
$l_i^{(1)},\ldots ,l_i^{(d)} $
the side lengths of the cuboid
![]() $\tilde z^o_{(i)}$
, where
$\tilde z^o_{(i)}$
, where
![]() $l_i^{(k)}$
is the length of the sides that are parallel to
$l_i^{(k)}$
is the length of the sides that are parallel to
![]() $e_k$
,
$e_k$
,
![]() $k\in \{ 1,\ldots , d\}$
,
$k\in \{ 1,\ldots , d\}$
,
![]() $i\in \mathbb{Z}$
. The following technical lemma prepares us for the proof of Theorem 4.
$i\in \mathbb{Z}$
. The following technical lemma prepares us for the proof of Theorem 4.
Lemma 2. With the assumptions of Theorem 3,
Proof. Fix some
![]() $k\in \{1,\ldots , d\}$
and, using the notation in the proof of Theorem 3, consider (13), which expresses the growth of the length
$k\in \{1,\ldots , d\}$
and, using the notation in the proof of Theorem 3, consider (13), which expresses the growth of the length
![]() $l_i^{(k)}$
if
$l_i^{(k)}$
if
![]() $t_i=t^{k+}_m$
or
$t_i=t^{k+}_m$
or
![]() $t_i =t^{k-}_m$
for some
$t_i =t^{k-}_m$
for some
![]() $m \in \mathbb{N}_0$
. The index k is chosen with probability
$m \in \mathbb{N}_0$
. The index k is chosen with probability
![]() $p_k$
. Obviously,
$p_k$
. Obviously,
![]() $\big(p_k\prod_{j=i}^0 R_j\big)^{-1}\,{>}\,1$
. Hence, the events
$\big(p_k\prod_{j=i}^0 R_j\big)^{-1}\,{>}\,1$
. Hence, the events
![]() $B_i:\!=\{\kappa_i>d,\,t_i=t^{k+}_m\text{ or }t_i=t^{k-}_m\text{ for some }m\in\mathbb{N}_0\}$
,
$B_i:\!=\{\kappa_i>d,\,t_i=t^{k+}_m\text{ or }t_i=t^{k-}_m\text{ for some }m\in\mathbb{N}_0\}$
,
![]() $i\in \mathbb{Z}$
, which are independent, have a strictly positive probability that does not depend on i. Thus, the Borel–Cantelli lemma yields
$i\in \mathbb{Z}$
, which are independent, have a strictly positive probability that does not depend on i. Thus, the Borel–Cantelli lemma yields
![]() $\mathbb{P}\big(\bigcap_{n\leq 0}\bigcup_{i\leq n}B_i\big) = 1$
, i.e. there are infinitely many of the
$\mathbb{P}\big(\bigcap_{n\leq 0}\bigcup_{i\leq n}B_i\big) = 1$
, i.e. there are infinitely many of the
![]() $B_i$
a.s. This, together with the monotonicity of the sequence
$B_i$
a.s. This, together with the monotonicity of the sequence
![]() $(l_i^{(k)}, \, i\in \mathbb{Z})$
yields that, for all
$(l_i^{(k)}, \, i\in \mathbb{Z})$
yields that, for all
![]() $k\in \{1,\ldots , d\}$
,
$k\in \{1,\ldots , d\}$
,
![]() $\mathbb{P}(\text{there exists }i_0(k)\in\mathbb{Z}\colon \text{ for all }i\leq i_0(k), l_i^{(k)}>d)=1$
, and hence
$\mathbb{P}(\text{there exists }i_0(k)\in\mathbb{Z}\colon \text{ for all }i\leq i_0(k), l_i^{(k)}>d)=1$
, and hence
![]() $\mathbb{P}(\text{for all }k\in\{1,\ldots,d\}\text{ there exists }i_0(k)\in\mathbb{Z}\colon \text{ for all }i\leq i_0(k), l_i^{(k)} > d) = 1$
. Because there are only finitely many k, the assertion of the lemma follows.
$\mathbb{P}(\text{for all }k\in\{1,\ldots,d\}\text{ there exists }i_0(k)\in\mathbb{Z}\colon \text{ for all }i\leq i_0(k), l_i^{(k)} > d) = 1$
. Because there are only finitely many k, the assertion of the lemma follows.
Lemma 2 can be used to check the sufficient condition (8) when the functional G is chosen as a function of the side lengths of the zero-cell. Here we consider the important cases of the intrinsic volumes
![]() $V_n$
,
$V_n$
,
![]() $n\in \{ 1,\ldots ,d \}$
. The functional
$n\in \{ 1,\ldots ,d \}$
. The functional
![]() $V_d$
is the volume,
$V_d$
is the volume,
![]() $V_1$
the mean width (or breadth) up to a constant factor. For
$V_1$
the mean width (or breadth) up to a constant factor. For
![]() $n=3$
the intrinsic volume
$n=3$
the intrinsic volume
![]() $V_2$
is, up to a constant factor, the surface area. The intrinsic volume
$V_2$
is, up to a constant factor, the surface area. The intrinsic volume
![]() $V_0$
is the Euler characteristic which has the value 1 for all nonempty convex sets, and hence it is clear that for
$V_0$
is the Euler characteristic which has the value 1 for all nonempty convex sets, and hence it is clear that for
![]() $G=V_0$
the sufficient condition (8) is not satisfied.
$G=V_0$
the sufficient condition (8) is not satisfied.
A definition of the intrinsic volumes for convex bodies can be found in [Reference Schneider and Weil25]. Here we make use of a formula for cuboids which is a particular case of the formula for polytopes, see [Reference Klain and Rota8, (4.9)] or [Reference Schneider and Weil25, (14.35)]. For
![]() $n\geq 1$
,
$n\geq 1$
,
 \begin{equation} V_n (\tilde z^o_{(i)}) = \sum_{1\leq k_1<\cdots <k_n \leq d}\ \prod_{j=1}^n l_i^{(k_j)} .\end{equation}
\begin{equation} V_n (\tilde z^o_{(i)}) = \sum_{1\leq k_1<\cdots <k_n \leq d}\ \prod_{j=1}^n l_i^{(k_j)} .\end{equation}
Theorem 4.
Let
![]() $\Lambda$
be a translation-invariant measure on the space of hyperplanes in
$\Lambda$
be a translation-invariant measure on the space of hyperplanes in
![]() $\mathbb{R}^d$
satisfying (1), where
$\mathbb{R}^d$
satisfying (1), where
![]() $\varphi$
is a Mondrian directional distribution (11). Then, for all
$\varphi$
is a Mondrian directional distribution (11). Then, for all
![]() $n\in \{1,\ldots ,d\}$
, there exists a Markov tessellation-valued process
$n\in \{1,\ldots ,d\}$
, there exists a Markov tessellation-valued process
![]() $(T_t,\, t>0)$
which is an (L-
$(T_t,\, t>0)$
which is an (L-
![]() $V_n$
) (D-
$V_n$
) (D-
![]() $\Lambda$
) cell division process according to Definition 2.
$\Lambda$
) cell division process according to Definition 2.
Proof. It is sufficient to show that (8) is satisfied for
![]() $G=V_n$
for all
$G=V_n$
for all
![]() $n\in \{ 1,\ldots ,d \}$
. For
$n\in \{ 1,\ldots ,d \}$
. For
![]() $n=1$
it follows immediately from Theorem 3. For
$n=1$
it follows immediately from Theorem 3. For
![]() $n \in\{2,\ldots ,k\}$
and
$n \in\{2,\ldots ,k\}$
and
![]() $i\in \mathbb{Z}$
,
$i\in \mathbb{Z}$
,
 $$ \Bigg(\sum_{k_1<\cdots<k_n}\,\prod_{j=1}^n l_i^{(k_j)}\Bigg) - \sum_{k=1}^d l_i^{(k)} = \frac{1}{\begin{pmatrix}d-1\\n-1 \end{pmatrix}}\sum_{k=1}^d l_i^{(k)} \Bigg(\sum_{{k_1<\cdots<k_{n-1}},\,{k_j\not= k}}\Bigg(\frac{\begin{pmatrix}d\\n \end{pmatrix}}{d}\prod_{j=1}^{n-1}l_i^{(k_j)}-1\Bigg)\Bigg). $$
$$ \Bigg(\sum_{k_1<\cdots<k_n}\,\prod_{j=1}^n l_i^{(k_j)}\Bigg) - \sum_{k=1}^d l_i^{(k)} = \frac{1}{\begin{pmatrix}d-1\\n-1 \end{pmatrix}}\sum_{k=1}^d l_i^{(k)} \Bigg(\sum_{{k_1<\cdots<k_{n-1}},\,{k_j\not= k}}\Bigg(\frac{\begin{pmatrix}d\\n \end{pmatrix}}{d}\prod_{j=1}^{n-1}l_i^{(k_j)}-1\Bigg)\Bigg). $$
Note that
![]() ${\begin{pmatrix}d\\d \end{pmatrix}}/d =1/d$
and
${\begin{pmatrix}d\\d \end{pmatrix}}/d =1/d$
and
![]() $\begin{pmatrix}d\\n \end{pmatrix}/d \geq 1$
for
$\begin{pmatrix}d\\n \end{pmatrix}/d \geq 1$
for
![]() $n\in \{ 1,\ldots , d-1\}$
. By Lemma 2 there exists a.s. an
$n\in \{ 1,\ldots , d-1\}$
. By Lemma 2 there exists a.s. an
![]() $i_0\in \mathbb{Z}$
such that, for all
$i_0\in \mathbb{Z}$
such that, for all
![]() $i\leq i_0$
and all
$i\leq i_0$
and all
![]() $k\in \{1,\ldots , d\}$
, the side lengths
$k\in \{1,\ldots , d\}$
, the side lengths
![]() $ l_i^{(k)} > d$
, which implies that the difference on the left-hand side is positive. Recall that
$ l_i^{(k)} > d$
, which implies that the difference on the left-hand side is positive. Recall that
![]() $S_i=\sum_{k=1}^d l_i^{(k)}$
for all
$S_i=\sum_{k=1}^d l_i^{(k)}$
for all
![]() $i\in \mathbb{Z}$
, and that in the proof of Theorem 3 it was shown that
$i\in \mathbb{Z}$
, and that in the proof of Theorem 3 it was shown that
![]() $\sum_{i\leq 0}S_i^{-1}<\infty$
a.s. Hence, for
$\sum_{i\leq 0}S_i^{-1}<\infty$
a.s. Hence, for
![]() $n \in\{2,\ldots ,k\}$
,
$n \in\{2,\ldots ,k\}$
,
![]() $\sum_{i\leq 0}\big(\sum_{k_1<\cdots<k_n}\prod_{j=1}^n l_i^{(k_j)}\big)^{-1}<\infty$
a.s. also, and, by (15),
$\sum_{i\leq 0}\big(\sum_{k_1<\cdots<k_n}\prod_{j=1}^n l_i^{(k_j)}\big)^{-1}<\infty$
a.s. also, and, by (15),
![]() $\sum_{i\leq 0}V_n\big(\tilde z^o_{(i)}\big)^{-1} < \infty$
a.s.
$\sum_{i\leq 0}V_n\big(\tilde z^o_{(i)}\big)^{-1} < \infty$
a.s.
Remark 1. Theorem 4 can easily be generalized to (L-
![]() $V_n^\alpha$
) (D-
$V_n^\alpha$
) (D-
![]() $\Lambda$
) cell division processes for exponents
$\Lambda$
) cell division processes for exponents
![]() $\alpha \geq 1$
. The larger
$\alpha \geq 1$
. The larger
![]() $\alpha$
is, the longer will be the life time of cells z with
$\alpha$
is, the longer will be the life time of cells z with
![]() $V_n(z) <1$
and the shorter the life time if
$V_n(z) <1$
and the shorter the life time if
![]() $V_n(z)>1$
.
$V_n(z)>1$
.
Note that for the Mondrian distribution defined in (11) with
![]() $p_1=\ldots =p_d= 1/d$
, the (L-
$p_1=\ldots =p_d= 1/d$
, the (L-
![]() $V_1$
) (D-
$V_1$
) (D-
![]() $\Lambda$
) cell division process is, up to a scaling factor, the same as the STIT tessellation process driven by
$\Lambda$
) cell division process is, up to a scaling factor, the same as the STIT tessellation process driven by
![]() $\Lambda$
, which is a (L-
$\Lambda$
, which is a (L-
![]() $\Lambda$
) (D-
$\Lambda$
) (D-
![]() $\Lambda$
) cell division process.
$\Lambda$
) cell division process.
5.2. Distribution of cell volumes
Now we consider the particular cell division process in
![]() $\mathbb{R}^d$
with volume-weighted life time distribution (L-
$\mathbb{R}^d$
with volume-weighted life time distribution (L-
![]() $V_d$
) and (D-
$V_d$
) and (D-
![]() $\Lambda $
), with a Mondrian directional distribution (11). We make use of an idea, used in [Reference Cowan3], developed for so-called ‘geometry-independent apportionment of volume’ (GIA), which means a division rule such that the ratio of the volume of a daughter cell and the volume of the mother cell is uniformly distributed on the interval (0,1).
$\Lambda $
), with a Mondrian directional distribution (11). We make use of an idea, used in [Reference Cowan3], developed for so-called ‘geometry-independent apportionment of volume’ (GIA), which means a division rule such that the ratio of the volume of a daughter cell and the volume of the mother cell is uniformly distributed on the interval (0,1).
In contrast to this, in Section 5.3 we consider an (L-
![]() $V_d$
) (D-
$V_d$
) (D-
![]() $\Lambda $
) process in a bounded window W and describe its relation to fragmentation.
$\Lambda $
) process in a bounded window W and describe its relation to fragmentation.
For a random stationary tessellation of
![]() $\mathbb{R}^d$
the concept of the ‘typical cell’ is formally defined using the Palm measure; see [Reference Schneider and Weil25, p. 450], for example. Intuitively, it can be imagined as a cell, chosen at random, where all cells have the same chance to be chosen. Let T be a random spatially stationary tessellation in
$\mathbb{R}^d$
the concept of the ‘typical cell’ is formally defined using the Palm measure; see [Reference Schneider and Weil25, p. 450], for example. Intuitively, it can be imagined as a cell, chosen at random, where all cells have the same chance to be chosen. Let T be a random spatially stationary tessellation in
![]() $\mathbb{R}^d$
with law
$\mathbb{R}^d$
with law
![]() $\mathbb{P}_T$
. Furthermore, let
$\mathbb{P}_T$
. Furthermore, let
![]() $c\colon{\mathcal{P}_d} \to \mathbb{R}^d$
be a center function, which means that c is measurable and translation covariant, i.e.
$c\colon{\mathcal{P}_d} \to \mathbb{R}^d$
be a center function, which means that c is measurable and translation covariant, i.e.
![]() $c(z+x)=c(z)+x$
for all
$c(z+x)=c(z)+x$
for all
![]() $z\in {\mathcal{P}_d}$
,
$z\in {\mathcal{P}_d}$
,
![]() $x\in \mathbb{R}^d$
. For example, c(z) can be chosen as the circumcenter of z. The intensity of the center points of cells of T is the mean number of those points per unit volume,
$x\in \mathbb{R}^d$
. For example, c(z) can be chosen as the circumcenter of z. The intensity of the center points of cells of T is the mean number of those points per unit volume,
![]() $\gamma_T :\!= \mathbb{E} \sum_{z\in T} \textbf{1}\{ c(z)\in [0,1]^d\}$
, where
$\gamma_T :\!= \mathbb{E} \sum_{z\in T} \textbf{1}\{ c(z)\in [0,1]^d\}$
, where
![]() $\textbf{1}\{ \ldots \}$
denotes the indicator function with value 1 if the condition in brackets is satisfied and 0 otherwise. Then the distribution
$\textbf{1}\{ \ldots \}$
denotes the indicator function with value 1 if the condition in brackets is satisfied and 0 otherwise. Then the distribution
![]() $\mathbb{Q}_T$
of the typical cell of T is defined by
$\mathbb{Q}_T$
of the typical cell of T is defined by
for all measurable sets
![]() $A\subseteq {\mathcal{P}_d}$
. A random polytope with law
$A\subseteq {\mathcal{P}_d}$
. A random polytope with law
![]() $\mathbb{Q}_T$
is called the typical cell of T.
$\mathbb{Q}_T$
is called the typical cell of T.
Lemma 3.
Let
![]() $\Lambda$
be a translation-invariant measure on the space of hyperplanes in
$\Lambda$
be a translation-invariant measure on the space of hyperplanes in
![]() $\mathbb{R}^d$
satisfying (1), where
$\mathbb{R}^d$
satisfying (1), where
![]() $\varphi$
is a Mondrian directional distribution (11), and let
$\varphi$
is a Mondrian directional distribution (11), and let
![]() $(T_t,\, t>0)$
be the (L-
$(T_t,\, t>0)$
be the (L-
![]() $V_d$
) (D-
$V_d$
) (D-
![]() $\Lambda $
) cell division process as described in the proof of Theorem 1. Then, for all
$\Lambda $
) cell division process as described in the proof of Theorem 1. Then, for all
![]() $t>0$
, the law of the volume
$t>0$
, the law of the volume
![]() $V_d(z)$
of the typical cell of
$V_d(z)$
of the typical cell of
![]() $T_t$
is the exponential distribution with parameter t, and the law of the volume
$T_t$
is the exponential distribution with parameter t, and the law of the volume
![]() $V_d(z^o_t)$
of the zero-cell of
$V_d(z^o_t)$
of the zero-cell of
![]() $T_t$
is the gamma distribution with parameter (2,t), which is also referred to as an Erlang distribution.
$T_t$
is the gamma distribution with parameter (2,t), which is also referred to as an Erlang distribution.
Proof. The volumes of cells of a tessellation
![]() $T_t$
,
$T_t$
,
![]() $t>0$
, are represented by the lengths of intervals on
$t>0$
, are represented by the lengths of intervals on
![]() $\mathbb{R}$
. The idea of the proof is the following: The tessellation
$\mathbb{R}$
. The idea of the proof is the following: The tessellation
![]() $T_t$
is mapped to a point process
$T_t$
is mapped to a point process
![]() $(y^{(j)},\, j \in \mathbb{Z})$
on
$(y^{(j)},\, j \in \mathbb{Z})$
on
![]() $\mathbb{R}$
such that the lengths of the intervals between adjacent points correspond to the volumes of the cells of
$\mathbb{R}$
such that the lengths of the intervals between adjacent points correspond to the volumes of the cells of
![]() $T_t$
.
$T_t$
.
In order to formalize this idea, it is an involved technical issue to bring these intervals into an appropriate linear order. As before, we start with the process of zero cells as defined in (10), and we use a method analogous to the one in the proof of Theorem 3. But here we consider the differences of volumes when cells are split.
If, for some
![]() ${\varepsilon} >0$
, the tessellation
${\varepsilon} >0$
, the tessellation
![]() $T_{\varepsilon}$
is mapped to a point process
$T_{\varepsilon}$
is mapped to a point process
![]() $(y_{\varepsilon} ^{(j)},\, j \in \mathbb{Z})$
on
$(y_{\varepsilon} ^{(j)},\, j \in \mathbb{Z})$
on
![]() $\mathbb{R}$
such that the lengths of the intervals between adjacent points correspond to the volumes of the cells of
$\mathbb{R}$
such that the lengths of the intervals between adjacent points correspond to the volumes of the cells of
![]() $T_{\varepsilon}$
, then the division of the cell volumes in the continuation of the cell division process corresponds to a Poisson point process that is superposed on
$T_{\varepsilon}$
, then the division of the cell volumes in the continuation of the cell division process corresponds to a Poisson point process that is superposed on
![]() $(y_{\varepsilon} ^{(j)},\, j \in \mathbb{Z})$
. Because this can be done for any
$(y_{\varepsilon} ^{(j)},\, j \in \mathbb{Z})$
. Because this can be done for any
![]() ${\varepsilon} >0$
, we can conclude that the cell volumes of
${\varepsilon} >0$
, we can conclude that the cell volumes of
![]() $T_t$
are represented by the lengths of the interval between two adjacent points of a Poisson point process. Summarizing the idea, we will show this for a Poisson point process on
$T_t$
are represented by the lengths of the interval between two adjacent points of a Poisson point process. Summarizing the idea, we will show this for a Poisson point process on
![]() $\mathbb{R}^d \times (0,\infty )$
with intensity measure
$\mathbb{R}^d \times (0,\infty )$
with intensity measure
![]() $\lambda \otimes \lambda_+$
.
$\lambda \otimes \lambda_+$
.
Fix an
![]() ${\varepsilon} >0$
and
${\varepsilon} >0$
and
![]() $i\in \mathbb{Z}$
such that
$i\in \mathbb{Z}$
such that
![]() $\tau_i\leq {\varepsilon} < \tau_{i+1}$
, where
$\tau_i\leq {\varepsilon} < \tau_{i+1}$
, where
![]() $\tau_i$
is defined in (9) with
$\tau_i$
is defined in (9) with
![]() $G=V_d$
. Let
$G=V_d$
. Let
![]() $\hat y_{\varepsilon}^{(\!{-}1)} < 0 < \hat y_{\varepsilon}^{(0)}$
be real valued such that
$\hat y_{\varepsilon}^{(\!{-}1)} < 0 < \hat y_{\varepsilon}^{(0)}$
be real valued such that
![]() $\hat y_{\varepsilon}^{(0)} - \hat y_{\varepsilon}^{(\!{-}1)}= V_d (z_{\tau_i})$
, and 0 is uniformly distributed in the interval
$\hat y_{\varepsilon}^{(0)} - \hat y_{\varepsilon}^{(\!{-}1)}= V_d (z_{\tau_i})$
, and 0 is uniformly distributed in the interval
![]() $\big(\hat y_{\varepsilon}^{(\!{-}1)}, \hat y_{\varepsilon}^{(0)}\big)$
.
$\big(\hat y_{\varepsilon}^{(\!{-}1)}, \hat y_{\varepsilon}^{(0)}\big)$
.
Initialize counters
![]() $r:\!=0$
and
$r:\!=0$
and
![]() $\ell :\!=1$
. If, in (12),
$\ell :\!=1$
. If, in (12),
![]() $t_i =t^{k+}_m$
for some k and m, then put
$t_i =t^{k+}_m$
for some k and m, then put
![]() $\hat y_{\varepsilon}^{(1)}:\!=\hat y_{\varepsilon}^{(0)}+V_d(z_{\tau_{i-1}}\setminus z_{\tau_i})$
,
$\hat y_{\varepsilon}^{(1)}:\!=\hat y_{\varepsilon}^{(0)}+V_d(z_{\tau_{i-1}}\setminus z_{\tau_i})$
,
![]() $t^{(0)} :\!= \tau_i$
, and update
$t^{(0)} :\!= \tau_i$
, and update
![]() $r:\!=1$
. If
$r:\!=1$
. If
![]() $t_i =t^{k-}_m$
for some k and m, then define
$t_i =t^{k-}_m$
for some k and m, then define
![]() $\hat y_{\varepsilon}^{(\!{-}2)}:\!=\hat y_{\varepsilon}^{(\!{-}1)}-V_d(z_{\tau_{i-1}}\setminus z_{\tau_i})$
,
$\hat y_{\varepsilon}^{(\!{-}2)}:\!=\hat y_{\varepsilon}^{(\!{-}1)}-V_d(z_{\tau_{i-1}}\setminus z_{\tau_i})$
,
![]() $t^{(\!{-}1)} :\!= \tau_i$
, and update
$t^{(\!{-}1)} :\!= \tau_i$
, and update
![]() $\ell:\!=2$
.
$\ell:\!=2$
.
Having defined
![]() $\big(\hat y_{\varepsilon}^{(\!{-}\ell)},t^{(\!{-}\ell)}\big),\ldots,\big(\hat y_{\varepsilon}^{(r)},t^{(r)}\big)$
for some
$\big(\hat y_{\varepsilon}^{(\!{-}\ell)},t^{(\!{-}\ell)}\big),\ldots,\big(\hat y_{\varepsilon}^{(r)},t^{(r)}\big)$
for some
![]() $\ell \in \mathbb{N}_0$
and
$\ell \in \mathbb{N}_0$
and
![]() $r\in \mathbb{N}_0$
, the next item of the sequence is that if, in (12),
$r\in \mathbb{N}_0$
, the next item of the sequence is that if, in (12),
![]() $t_{i-r-\ell -1} =t^{k+}_m$
for some k and m, then
$t_{i-r-\ell -1} =t^{k+}_m$
for some k and m, then
![]() $\hat y_{\varepsilon}^{(r+1)}:\!=\hat y_{\varepsilon}^{(r)}+V_d(z_{\tau_{i-r-\ell -2}}\setminus z_{\tau_{i-r-\ell -1}})$
,
$\hat y_{\varepsilon}^{(r+1)}:\!=\hat y_{\varepsilon}^{(r)}+V_d(z_{\tau_{i-r-\ell -2}}\setminus z_{\tau_{i-r-\ell -1}})$
,
![]() $t^{(r+1)}:\!=\tau_{i-r-\ell -1}$
, and update
$t^{(r+1)}:\!=\tau_{i-r-\ell -1}$
, and update
![]() $r:\!=r+1$
. If
$r:\!=r+1$
. If
![]() $t_{i-r-\ell -1} =t^{k-}_m$
for some k and m, then
$t_{i-r-\ell -1} =t^{k-}_m$
for some k and m, then
![]() $\hat y_{\varepsilon}^{(\!{-}\ell -1)}:\!=\hat y_{\varepsilon}^{(\!{-}\ell )}-V_d(z_{\tau_{i-r-\ell -2}}\setminus z_{\tau_{i-r-\ell -1}})$
,
$\hat y_{\varepsilon}^{(\!{-}\ell -1)}:\!=\hat y_{\varepsilon}^{(\!{-}\ell )}-V_d(z_{\tau_{i-r-\ell -2}}\setminus z_{\tau_{i-r-\ell -1}})$
,
![]() $t^{(\!{-}\ell -1)}:\!=\tau_{i-r-\ell -1}$
, and update
$t^{(\!{-}\ell -1)}:\!=\tau_{i-r-\ell -1}$
, and update
![]() $\ell :\!=\ell +1$
.
$\ell :\!=\ell +1$
.
This yields the sequence
![]() $((\hat y_{\varepsilon}^{(j)},t^{(j)}) ,\, j\in \mathbb{Z})$
pertaining to the process of zero-cells. It has to be complemented by the points which correspond to the divisions of the cells
$((\hat y_{\varepsilon}^{(j)},t^{(j)}) ,\, j\in \mathbb{Z})$
pertaining to the process of zero-cells. It has to be complemented by the points which correspond to the divisions of the cells
![]() $\text{cl}(z_{\tau_{i-r-\ell -2}}\setminus z_{\tau_{i-r-\ell -1}})$
in the time interval
$\text{cl}(z_{\tau_{i-r-\ell -2}}\setminus z_{\tau_{i-r-\ell -1}})$
in the time interval
![]() $(\tau_{i-r-\ell -1}, t)$
.
$(\tau_{i-r-\ell -1}, t)$
.
This can be described as follows. The volume of the cell
![]() $\text{cl}(z_{\tau_{i-r-\ell -2}}\setminus z_{\tau_{i-r-\ell -1}})$
equals the length of the interval
$\text{cl}(z_{\tau_{i-r-\ell -2}}\setminus z_{\tau_{i-r-\ell -1}})$
equals the length of the interval
![]() $(\hat y_{\varepsilon}^{(r)}, \hat y_{\varepsilon}^{(r+1)})$
or
$(\hat y_{\varepsilon}^{(r)}, \hat y_{\varepsilon}^{(r+1)})$
or
![]() $(\hat y_{\varepsilon}^{(\!{-}\ell -1)},\hat y_{\varepsilon}^{(\!{-}\ell )})$
, respectively. For the sake of simplicity, in the following we consider only the part of
$(\hat y_{\varepsilon}^{(\!{-}\ell -1)},\hat y_{\varepsilon}^{(\!{-}\ell )})$
, respectively. For the sake of simplicity, in the following we consider only the part of
![]() $((\hat y_{\varepsilon}^{(j)},t^{(j)}),\,j\in\mathbb{Z})$
that belongs to
$((\hat y_{\varepsilon}^{(j)},t^{(j)}),\,j\in\mathbb{Z})$
that belongs to
![]() $(0,\infty )\times (0,\infty )$
. The other part on
$(0,\infty )\times (0,\infty )$
. The other part on
![]() $(\!{-}\infty ,0)\times (0,\infty )$
can be dealt with quite analogously. When the cell
$(\!{-}\infty ,0)\times (0,\infty )$
can be dealt with quite analogously. When the cell
![]() $\text{cl}(z_{\tau_{i-r-\ell -2}}\setminus z_{\tau_{i-r-\ell -1}})$
is divided by a hyperplane, the respective interval is divided by a point such that the two new interval lengths equal the two volumes of the daughter cells. We define the new interval that is closer to
$\text{cl}(z_{\tau_{i-r-\ell -2}}\setminus z_{\tau_{i-r-\ell -1}})$
is divided by a hyperplane, the respective interval is divided by a point such that the two new interval lengths equal the two volumes of the daughter cells. We define the new interval that is closer to
![]() $0\in \mathbb{R}$
to pertain to the daughter cell which is contained in the half-space of the dividing hyperplane that contains the origin
$0\in \mathbb{R}$
to pertain to the daughter cell which is contained in the half-space of the dividing hyperplane that contains the origin
![]() $o\in\mathbb{R}^d$
. The point dividing the interval is marked with the birth time of the hyperplane dividing the cell. Thus, the interval
$o\in\mathbb{R}^d$
. The point dividing the interval is marked with the birth time of the hyperplane dividing the cell. Thus, the interval
![]() $(\hat y_{\varepsilon}^{(r)}, \hat y_{\varepsilon}^{(r+1)})$
is divided after a life time that is exponentially distributed with the parameter
$(\hat y_{\varepsilon}^{(r)}, \hat y_{\varepsilon}^{(r+1)})$
is divided after a life time that is exponentially distributed with the parameter
![]() $\hat y_{\varepsilon}^{(r+1)}- \hat y_{\varepsilon}^{(r)}$
, and the dividing point is (due to the translation invariance of
$\hat y_{\varepsilon}^{(r+1)}- \hat y_{\varepsilon}^{(r)}$
, and the dividing point is (due to the translation invariance of
![]() $\Lambda$
) uniformly distributed in this interval. The new daughter intervals are subsequently divided following analogous rules. Thus, the birth-time-marked point process appearing in the interval
$\Lambda$
) uniformly distributed in this interval. The new daughter intervals are subsequently divided following analogous rules. Thus, the birth-time-marked point process appearing in the interval
![]() $(\hat y_{\varepsilon}^{(r)}, \hat y_{\varepsilon}^{(r+1)})$
has the same distribution as the Poisson point process on
$(\hat y_{\varepsilon}^{(r)}, \hat y_{\varepsilon}^{(r+1)})$
has the same distribution as the Poisson point process on
![]() $(\hat y_{\varepsilon}^{(r)}, \hat y_{\varepsilon}^{(r+1)})\times (\tau_{i-r-\ell -1}, t)$
, with the two-dimensional Lebesgue measure (restricted to this set) as its intensity measure.
$(\hat y_{\varepsilon}^{(r)}, \hat y_{\varepsilon}^{(r+1)})\times (\tau_{i-r-\ell -1}, t)$
, with the two-dimensional Lebesgue measure (restricted to this set) as its intensity measure.
Taking all the marked points together, we obtain a point process
![]() $Y_{\varepsilon} :\!= ((y_{\varepsilon}^{(j)}, t^{(j)}),\, j\in \mathbb{Z} )$
. Given this point process for some time
$Y_{\varepsilon} :\!= ((y_{\varepsilon}^{(j)}, t^{(j)}),\, j\in \mathbb{Z} )$
. Given this point process for some time
![]() ${\varepsilon} >0$
, and regarding the independence assumptions in Definition 2, the generation of the point process
${\varepsilon} >0$
, and regarding the independence assumptions in Definition 2, the generation of the point process
![]() $Y_t =((y_t^{(j)}, t^{(j)}),\, j\in \mathbb{Z} )$
for
$Y_t =((y_t^{(j)}, t^{(j)}),\, j\in \mathbb{Z} )$
for
![]() $t>{\varepsilon} $
can be described using an auxiliary Poisson point process
$t>{\varepsilon} $
can be described using an auxiliary Poisson point process
![]() $\Phi^*$
on
$\Phi^*$
on
![]() $\mathbb{R} \times (0,\infty)$
with intensity measure
$\mathbb{R} \times (0,\infty)$
with intensity measure
![]() $\lambda \otimes \lambda_+$
.
$\lambda \otimes \lambda_+$
.
For all
![]() $0<{\varepsilon} <t$
, let
$0<{\varepsilon} <t$
, let
![]() $\Phi^*_{({\varepsilon} ,t)} :\!= \{ (x,t^{\prime})\in \Phi^* \colon {\varepsilon} <t^{\prime} <t \}$
. We obtain
$\Phi^*_{({\varepsilon} ,t)} :\!= \{ (x,t^{\prime})\in \Phi^* \colon {\varepsilon} <t^{\prime} <t \}$
. We obtain
![]() $Y_t \stackrel{\textrm{D}}{=} Y_{\varepsilon} \cup \Phi^*_{({\varepsilon} ,t)}$
, which is the superposition of two independent point processes.
$Y_t \stackrel{\textrm{D}}{=} Y_{\varepsilon} \cup \Phi^*_{({\varepsilon} ,t)}$
, which is the superposition of two independent point processes.
The sequence
![]() $((\hat y_{\varepsilon}^{(j)},t^{(j)}) ,\, j\in \mathbb{Z})$
pertaining to the process of zero cells is monotone in
$((\hat y_{\varepsilon}^{(j)},t^{(j)}) ,\, j\in \mathbb{Z})$
pertaining to the process of zero cells is monotone in
![]() ${\varepsilon}$
in the following sense. For
${\varepsilon}$
in the following sense. For
![]() ${\varepsilon}_2 < {\varepsilon}_1$
the sequence
${\varepsilon}_2 < {\varepsilon}_1$
the sequence
![]() $((\hat y_{{\varepsilon}_2}^{(j)},t^{(j)}) ,\, j\in \mathbb{Z})$
emerges from
$((\hat y_{{\varepsilon}_2}^{(j)},t^{(j)}) ,\, j\in \mathbb{Z})$
emerges from
![]() $((\hat y_{{\varepsilon}_1}^{(i)},t^{(i)}) ,\, i\in \mathbb{Z})$
by deleting the points with
$((\hat y_{{\varepsilon}_1}^{(i)},t^{(i)}) ,\, i\in \mathbb{Z})$
by deleting the points with
![]() $t^{(i+1)} >{\varepsilon}_2$
for
$t^{(i+1)} >{\varepsilon}_2$
for
![]() $i\geq 0$
or
$i\geq 0$
or
![]() $t^{(i-1)} >{\varepsilon}_2$
for
$t^{(i-1)} >{\varepsilon}_2$
for
![]() $i< 0$
, followed by a respective rearrangement of the indexes
$i< 0$
, followed by a respective rearrangement of the indexes
![]() $i\in \mathbb{Z}$
. Accordingly,
$i\in \mathbb{Z}$
. Accordingly,
![]() $Y_{{\varepsilon}_2}=((y_{{\varepsilon}_2}^{(j)}, t^{(j)}),\, j\in \mathbb{Z} )$
can, up to a rearrangement of the indexes, be considered as a subsequence of
$Y_{{\varepsilon}_2}=((y_{{\varepsilon}_2}^{(j)}, t^{(j)}),\, j\in \mathbb{Z} )$
can, up to a rearrangement of the indexes, be considered as a subsequence of
![]() $Y_{{\varepsilon}_1}=((y_{{\varepsilon}_1}^{(j)}, t^{(j)}),\, j\in \mathbb{Z} )$
.
$Y_{{\varepsilon}_1}=((y_{{\varepsilon}_1}^{(j)}, t^{(j)}),\, j\in \mathbb{Z} )$
.
Denoting by
![]() $Y_{({\varepsilon}_2 ,{\varepsilon}_1)}$
the difference between
$Y_{({\varepsilon}_2 ,{\varepsilon}_1)}$
the difference between
![]() $Y_{{\varepsilon}_1}$
and
$Y_{{\varepsilon}_1}$
and
![]() $Y_{{\varepsilon}_2}$
, we can write
$Y_{{\varepsilon}_2}$
, we can write
where the superposed point processes are independent. This yields that
![]() $Y_{({\varepsilon}_2 ,{\varepsilon}_1)} \stackrel{\textrm{D}}{=} \Phi^*_{({\varepsilon}_2 ,{\varepsilon}_1)}$
. Intuitively, this means that the sequence
$Y_{({\varepsilon}_2 ,{\varepsilon}_1)} \stackrel{\textrm{D}}{=} \Phi^*_{({\varepsilon}_2 ,{\varepsilon}_1)}$
. Intuitively, this means that the sequence
![]() $((\hat y_{{\varepsilon}_1}^{(i)},t^{(i)}) ,\, i\in \mathbb{Z})$
pertaining to the process of zero-cells until time
$((\hat y_{{\varepsilon}_1}^{(i)},t^{(i)}) ,\, i\in \mathbb{Z})$
pertaining to the process of zero-cells until time
![]() ${\varepsilon}_1$
is consistent with the Poisson point process properties, which are characteristic for the consecutive division of cell volumes.
${\varepsilon}_1$
is consistent with the Poisson point process properties, which are characteristic for the consecutive division of cell volumes.
Because this holds for all
![]() ${\varepsilon}_2 > {\varepsilon}_1 >0$
, we have shown that
${\varepsilon}_2 > {\varepsilon}_1 >0$
, we have shown that
![]() $Y_t=((y_t^{(j)}, t^{(j)}),\, j\in \mathbb{Z})$
is a Poisson point process on
$Y_t=((y_t^{(j)}, t^{(j)}),\, j\in \mathbb{Z})$
is a Poisson point process on
![]() $\mathbb{R} \times (0,t)$
with intensity measure
$\mathbb{R} \times (0,t)$
with intensity measure
![]() $\lambda \otimes \lambda_{(0,t)}$
, where
$\lambda \otimes \lambda_{(0,t)}$
, where
![]() $\lambda_{(0,t)}$
denotes the restriction of the Lebesgue measure to the interval (0,t). Hence, the point process
$\lambda_{(0,t)}$
denotes the restriction of the Lebesgue measure to the interval (0,t). Hence, the point process
![]() $(y_t^{(j)},\, j\in \mathbb{Z})$
of points projected onto
$(y_t^{(j)},\, j\in \mathbb{Z})$
of points projected onto
![]() $\mathbb{R}$
is a homogeneous Poisson point process with intensity measure
$\mathbb{R}$
is a homogeneous Poisson point process with intensity measure
![]() $t\lambda$
, and therefore the length of the typical interval between two points is exponentially distributed with parameter t, while the length of the interval containing the origin o has a gamma distribution with parameter (2, t).
$t\lambda$
, and therefore the length of the typical interval between two points is exponentially distributed with parameter t, while the length of the interval containing the origin o has a gamma distribution with parameter (2, t).
Cell division processes are potential models for real crack or fracture patterns appearing in materials science, geology, soft matter, or nanotechnology. The examples considered in [Reference León, Nagel, Ohser and Arscott12, Reference Nagel, Mecke, Ohser and Weiß20] illustrate that a useful and simple initial goodness-of-fit criterion for such models is the coefficient of variation (CV) of the volume of the typical cell, and it became obvious that the CV of STIT is too large compared to the CV for data of real crack patterns.
Corollary 2.
With the assumptions of Lemma 3, for all
![]() $t>0$
,
$t>0$
,
where z is a random cuboid with the distribution of the typical cell of
![]() $T_t$
, and
$T_t$
, and
![]() $\text{Var}$
denotes the variance of a random variable.
$\text{Var}$
denotes the variance of a random variable.
For a cell division process with (L-
![]() $\Lambda$
) (D-
$\Lambda$
) (D-
![]() $\Lambda$
), which is the STIT tessellation process, at any time
$\Lambda$
), which is the STIT tessellation process, at any time
![]() $t>0$
the typical cell has the same distribution as the typical cell of Poisson hyperplane tessellation for the same
$t>0$
the typical cell has the same distribution as the typical cell of Poisson hyperplane tessellation for the same
![]() $\Lambda$
at the same time [Reference Nagel and Weiß21]. Hence, for the translation-invariant measure
$\Lambda$
at the same time [Reference Nagel and Weiß21]. Hence, for the translation-invariant measure
![]() $\Lambda$
satisfying (1) where
$\Lambda$
satisfying (1) where
![]() $\varphi$
is a Mondrian directional distribution (11), the CV of the volume of the typical cell equals
$\varphi$
is a Mondrian directional distribution (11), the CV of the volume of the typical cell equals
![]() $\text{CV}\big(\prod_{j=1}^d Z_j\big)$
, where
$\text{CV}\big(\prod_{j=1}^d Z_j\big)$
, where
![]() $Z_1,\ldots ,Z_d$
are independent exponentially distributed random variables with the parameters
$Z_1,\ldots ,Z_d$
are independent exponentially distributed random variables with the parameters
![]() $p_1 t,\ldots ,p_d t$
, respectively. Thus
$p_1 t,\ldots ,p_d t$
, respectively. Thus
![]() $\text{CV}(V_d(z^{\text{STIT}}))=2^d -1$
, where
$\text{CV}(V_d(z^{\text{STIT}}))=2^d -1$
, where
![]() $z^{\text{STIT}}$
is a random cuboid with the distribution of the typical cell of the STIT tessellation.
$z^{\text{STIT}}$
is a random cuboid with the distribution of the typical cell of the STIT tessellation.
Note that these CVs depend neither on the time t nor on the probabilities
![]() $p_1 ,\ldots ,p_d$
. Obviously, for
$p_1 ,\ldots ,p_d$
. Obviously, for
![]() $d\geq 2$
the variability of the volume of the typical cell of the (L-
$d\geq 2$
the variability of the volume of the typical cell of the (L-
![]() $V_d$
) (D-
$V_d$
) (D-
![]() $\Lambda $
) cell division process is considerably smaller than that of STIT.
$\Lambda $
) cell division process is considerably smaller than that of STIT.
We remark that the method of the proof of Lemma 3 is crucially based on the above-mentioned GIA principle, and in our context this can only be applied to the volume of cells. Therefore, it can neither be used to deal with other intrinsic volumes of the typical cell of the (L-
![]() $V_d$
) (D-
$V_d$
) (D-
![]() $\Lambda $
) cell division process, nor on the typical cell of any (L-
$\Lambda $
) cell division process, nor on the typical cell of any (L-
![]() $V_n$
) (D-
$V_n$
) (D-
![]() $\Lambda $
) cell division process with
$\Lambda $
) cell division process with
![]() $n<d$
. In those cases the representation of the functional values by intervals on the real line does not yield a Poisson point process.
$n<d$
. In those cases the representation of the functional values by intervals on the real line does not yield a Poisson point process.
5.3. A cell division process in a bounded window W and its relation to fragmentation
Now consider a fixed window
![]() $W\in {\mathcal{P}_d}$
which is a cuboid with its sides parallel or orthogonal to all axes of
$W\in {\mathcal{P}_d}$
which is a cuboid with its sides parallel or orthogonal to all axes of
![]() $\mathbb{R}^d$
. An (L-
$\mathbb{R}^d$
. An (L-
![]() $V_d$
) (D-
$V_d$
) (D-
![]() $\Lambda $
) cell division process
$\Lambda $
) cell division process
![]() $(T_{W,t},\, t\geq 0)$
within W is launched with
$(T_{W,t},\, t\geq 0)$
within W is launched with
![]() $T_{W,0}:\!= \{W\}$
. Note that its distribution is different from
$T_{W,0}:\!= \{W\}$
. Note that its distribution is different from
![]() $(T_t \wedge W ,\, t>0)$
, which is the restriction to W of the (L-
$(T_t \wedge W ,\, t>0)$
, which is the restriction to W of the (L-
![]() $V_d$
) (D-
$V_d$
) (D-
![]() $\Lambda $
) cell division process
$\Lambda $
) cell division process
![]() $(T_t ,\, t>0)$
in the whole of
$(T_t ,\, t>0)$
in the whole of
![]() $\mathbb{R}^d$
.
$\mathbb{R}^d$
.
The process
![]() $(T_{W,t},\, t\geq 0)$
can be related to a particular case of a conservative fragmentation process as described in [Reference Bertoin1].
$(T_{W,t},\, t\geq 0)$
can be related to a particular case of a conservative fragmentation process as described in [Reference Bertoin1].
Let
![]() $G\colon {\mathcal{P}_d} \to [0,\infty )$
be a measurable functional defined on the set of polytopes, and assume that
$G\colon {\mathcal{P}_d} \to [0,\infty )$
be a measurable functional defined on the set of polytopes, and assume that
![]() $G(W) =1$
. For
$G(W) =1$
. For
![]() $t>0$
and
$t>0$
and
![]() $T_{W,t} =\{ z_1,\ldots ,z_n\}$
, define
$T_{W,t} =\{ z_1,\ldots ,z_n\}$
, define
![]() $\textbf{G}(T_{W,t}):\!=(G(z_{i_1}),\ldots,G(z_{i_n}),0,0,\ldots)$
such that
$\textbf{G}(T_{W,t}):\!=(G(z_{i_1}),\ldots,G(z_{i_n}),0,0,\ldots)$
such that
![]() $\{i_1,\ldots , i_n\} =\{ 1,\ldots ,n\}$
and
$\{i_1,\ldots , i_n\} =\{ 1,\ldots ,n\}$
and
![]() $G(z_{i_1})\geq \cdots \geq G(z_{i_n})$
.
$G(z_{i_1})\geq \cdots \geq G(z_{i_n})$
.
If we choose
![]() $G(z)=V_d(z)$
for
$G(z)=V_d(z)$
for
![]() $z\in {\mathcal{P}_d}$
, then the (L-
$z\in {\mathcal{P}_d}$
, then the (L-
![]() $V_d$
) (D-
$V_d$
) (D-
![]() $\Lambda $
) cell division process
$\Lambda $
) cell division process
![]() $(T_{W,t},\, t\geq 0)$
induces a pure jump Markov process
$(T_{W,t},\, t\geq 0)$
induces a pure jump Markov process
![]() $(\textbf{G}(T_{W,t}),\, t\geq 0)$
on
$(\textbf{G}(T_{W,t}),\, t\geq 0)$
on
![]() ${\mathfrak S}:\!= (0,\infty )^\mathbb{N}$
with the following properties:
${\mathfrak S}:\!= (0,\infty )^\mathbb{N}$
with the following properties:
-
(i)
 $\sum_{z \in T_{W,t}} G(z) =1$
for all
$\sum_{z \in T_{W,t}} G(z) =1$
for all
 $t\geq 0$
.
$t\geq 0$
. -
(ii) The holding time of a state
 $(G(z_{i_1}),\ldots,G(z_{i_n}),0,0,\ldots)$
is exponentially distributed with parameter 1.
$(G(z_{i_1}),\ldots,G(z_{i_n}),0,0,\ldots)$
is exponentially distributed with parameter 1. -
(iii) At the nth jump time
 $\tau_{n}$
,
$\tau_{n}$
,
 $n\in \mathbb{N}$
, the process jumps from a state
$n\in \mathbb{N}$
, the process jumps from a state
 $(G(z_{i_1}),\ldots,G(z_{i_n})$
,
$(G(z_{i_1}),\ldots,G(z_{i_n})$
,
 $0,0,\ldots)$
to
$0,0,\ldots)$
to
 $(G(z_{j_1}),\ldots,G(z_{j_{n+1}}),0,0,\ldots)$
by the following rule:
$(G(z_{j_1}),\ldots,G(z_{j_{n+1}}),0,0,\ldots)$
by the following rule:The index
 $i_k$
,
$i_k$
,
 $k\in \{ 1,\ldots , n\}$
, is chosen at random with probability
$k\in \{ 1,\ldots , n\}$
, is chosen at random with probability
 $G(z_{i_k})= G(z_{i_k})/\sum_{\ell \in \{ 1,\ldots , n\}}G(z_{i_\ell})$
. Then the cell
$G(z_{i_k})= G(z_{i_k})/\sum_{\ell \in \{ 1,\ldots , n\}}G(z_{i_\ell})$
. Then the cell
 $z_{i_k}$
is divided into two new fragments,
$z_{i_k}$
is divided into two new fragments,
 $z^{\prime}_{i_k}$
and
$z^{\prime}_{i_k}$
and
 $z^{\prime\prime}_{i_k}$
say, and (16)where U is a random variable, uniformly distributed on (0,1) and independent of all the other random variables considered here.
$z^{\prime\prime}_{i_k}$
say, and (16)where U is a random variable, uniformly distributed on (0,1) and independent of all the other random variables considered here. \begin{equation} (G(z^{\prime}_{i_k}), G(z^{\prime\prime}_{i_k})) = (U G(z_{i_k}), (1-U) G(z_{i_k})), \end{equation}
\begin{equation} (G(z^{\prime}_{i_k}), G(z^{\prime\prime}_{i_k})) = (U G(z_{i_k}), (1-U) G(z_{i_k})), \end{equation}
-
(iv) Putting the G-values of the
 $n+1$
cells into descending order yields the new state
$n+1$
cells into descending order yields the new state
 $(G(z_{j_1}),\ldots,G(z_{j_{n+1}}),0,0,\ldots)$
.
$(G(z_{j_1}),\ldots,G(z_{j_{n+1}}),0,0,\ldots)$
.
This shows that, according to [Reference Bertoin1, Definition 1.1], the process
![]() $(\textbf{G}(T_{W,t}),\, t\geq 0)$
is a self-similar fragmentation chain with index of self-similarity
$(\textbf{G}(T_{W,t}),\, t\geq 0)$
is a self-similar fragmentation chain with index of self-similarity
![]() $\alpha =1$
and the dislocation measure
$\alpha =1$
and the dislocation measure
![]() $\nu$
defined by (16), i.e.
$\nu$
defined by (16), i.e.
![]() $\nu$
is the law of
$\nu$
is the law of
![]() $(\xi,1-\xi,0,0,\ldots)$
, where
$(\xi,1-\xi,0,0,\ldots)$
, where
![]() $\xi$
is a random variable which is uniformly distributed on the interval
$\xi$
is a random variable which is uniformly distributed on the interval
![]() $\big[\frac{1}{2},1\big]$
.
$\big[\frac{1}{2},1\big]$
.
Note that if G is chosen as another intrinsic volume
![]() $V_n$
,
$V_n$
,
![]() $n<d$
, then
$n<d$
, then
![]() $\sum_{z \in T_{W,t}} G(z) \geq 1$
with ‘
$\sum_{z \in T_{W,t}} G(z) \geq 1$
with ‘
![]() $>$
’ after the first division. Then this is no longer the conservative scenario in the sense of [Reference Bertoin1].
$>$
’ after the first division. Then this is no longer the conservative scenario in the sense of [Reference Bertoin1].
6. Discussion and open problems
The ‘constructive proof’ of the existence result of Theorem 1 of a cell division process does not imply a uniqueness result. We conjecture that the distribution of the process is uniquely determined by G and
![]() $\Lambda$
, but it is an open problem whether for (L-G) and (D-
$\Lambda$
, but it is an open problem whether for (L-G) and (D-
![]() $\Lambda$
) other distributions of cell division processes also exist. Up to now, only the uniqueness of the (L-
$\Lambda$
) other distributions of cell division processes also exist. Up to now, only the uniqueness of the (L-
![]() $\Lambda$
) (D-
$\Lambda$
) (D-
![]() $\Lambda$
) cell division process has been shown, which is the STIT tessellation process driven by
$\Lambda$
) cell division process has been shown, which is the STIT tessellation process driven by
![]() $\Lambda$
.
$\Lambda$
.
Somehow related to the uniqueness problem is the question of whether the sufficient condition in (8) for the existence of an (L-G) (D-
![]() $\Lambda$
) cell division process is also a necessary one.
$\Lambda$
) cell division process is also a necessary one.
In a cell division process
![]() $(T_t,\, t>0)$
the cells z are divided subsequently as long as
$(T_t,\, t>0)$
the cells z are divided subsequently as long as
![]() $G(z)>0$
. Therefore, in general there will not be a limiting random tessellation for
$G(z)>0$
. Therefore, in general there will not be a limiting random tessellation for
![]() $t\to \infty$
. Thus the problem arises of whether there is a scaling of the process which stabilizes the one-dimensional distributions of the process or even yields a time-stationary process. For a tessellation
$t\to \infty$
. Thus the problem arises of whether there is a scaling of the process which stabilizes the one-dimensional distributions of the process or even yields a time-stationary process. For a tessellation
![]() $T\in \mathbb{T}$
the scaling by a factor
$T\in \mathbb{T}$
the scaling by a factor
![]() $c>0$
means
$c>0$
means
![]() $cT:\!= \{ cz;\, z\in T\}$
, with
$cT:\!= \{ cz;\, z\in T\}$
, with
![]() $cz:\!=\{ cx\colon x\in z\}$
.
$cz:\!=\{ cx\colon x\in z\}$
.
For the STIT tessellation process
![]() $(Y_t,\, t>0)$
driven by an arbitrary
$(Y_t,\, t>0)$
driven by an arbitrary
![]() $\Lambda$
satisfying (1) and (2), it was shown in [Reference Nagel and Weiß21] that
$\Lambda$
satisfying (1) and (2), it was shown in [Reference Nagel and Weiß21] that
![]() $t Y_t \stackrel{\textrm{D}}{=} Y_1$
for all
$t Y_t \stackrel{\textrm{D}}{=} Y_1$
for all
![]() $t>0$
. Furthermore, in [Reference Martínez and Nagel13] it was proven that for
$t>0$
. Furthermore, in [Reference Martínez and Nagel13] it was proven that for
![]() $a>1$
the process
$a>1$
the process
![]() $a^t Y_{a^t}$
is stationary in time.
$a^t Y_{a^t}$
is stationary in time.
For (L-
![]() $V_d$
) (D-
$V_d$
) (D-
![]() $\Lambda$
) and the Mondrian directional distribution, by Lemma 3, for all
$\Lambda$
) and the Mondrian directional distribution, by Lemma 3, for all
![]() $t>0$
and for the zero-cell
$t>0$
and for the zero-cell
![]() $z^0_t$
of
$z^0_t$
of
![]() $T_t$
, we have
$T_t$
, we have
![]() $t V_d (z^0_t)\stackrel{\textrm{D}}{=}V_d (z^0_1)$
and hence
$t V_d (z^0_t)\stackrel{\textrm{D}}{=}V_d (z^0_1)$
and hence
![]() $V_d (t^{1/d} z^0_t)\stackrel{\textrm{D}}{=}V_d (z^0_1)$
. This does not yet show a scaling property for the whole random tessellation
$V_d (t^{1/d} z^0_t)\stackrel{\textrm{D}}{=}V_d (z^0_1)$
. This does not yet show a scaling property for the whole random tessellation
![]() $T_t$
but we can see that, if there is a scaling factor, it can only be
$T_t$
but we can see that, if there is a scaling factor, it can only be
![]() $t^{1/d}$
.
$t^{1/d}$
.
Regarding tail triviality and other ergodic properties of the tessellations generated by cell division, the so-called method of encapsulation used in [Reference Martínez and Nagel14, Reference Martínez and Nagel15] cannot be applied here directly for models which are not spatially consistent. But the method used in the proof of Lemma 1 for zero-cells can be developed further.
Real crack structures, some of them mentioned in the introduction, show the tendency that the crack of a cell divides it close to the center. This is not yet incorporated in the models with a (D-
![]() $\Lambda$
) division rule where
$\Lambda$
) division rule where
![]() $\Lambda$
is a translation-invariant measure. Maybe this can be partially compensated in some cases using the life time rule (L-
$\Lambda$
is a translation-invariant measure. Maybe this can be partially compensated in some cases using the life time rule (L-
![]() $G^\alpha$
) instead of (L-G), with a large value of the exponent
$G^\alpha$
) instead of (L-G), with a large value of the exponent
![]() $\alpha$
. The impact of a large
$\alpha$
. The impact of a large
![]() $\alpha$
is that the life time of small cells is considerably increased while the life time of large cells is decreased compared to the setting with
$\alpha$
is that the life time of small cells is considerably increased while the life time of large cells is decreased compared to the setting with
![]() $\alpha =1$
, see also Remark 1. Thus, if the division of a mother cell generates a very small daughter cell and a relatively large one, then the larger one will be more frequently divided than the smaller one. This can result in a tessellation which is more ‘homogeneous’ in the sense that the sizes, measured by the function G, of the cells do not differ too much. And this can emulate a partition rule where the cells are divided by hyperplanes close to their center.
$\alpha =1$
, see also Remark 1. Thus, if the division of a mother cell generates a very small daughter cell and a relatively large one, then the larger one will be more frequently divided than the smaller one. This can result in a tessellation which is more ‘homogeneous’ in the sense that the sizes, measured by the function G, of the cells do not differ too much. And this can emulate a partition rule where the cells are divided by hyperplanes close to their center.
Nevertheless, it is desirable to develop models for cell division processes with alternative division rules as well as life time distributions. Here, a combination of the results of [Reference Georgii, Schreiber and Thäle4, Reference Schreiber and Thäle29] with the present approach could be promising. Simulation studies for tessellations in a bounded window of the plane
![]() $\mathbb{R}^2$
with several life time rules L and also a variety of division rules, aimed to adapt models to real structures, are presented in [Reference León, Montero and Nagel11, Reference León, Nagel, Ohser and Arscott12]. Code for simulation of those tessellations is available in [Reference León10].
$\mathbb{R}^2$
with several life time rules L and also a variety of division rules, aimed to adapt models to real structures, are presented in [Reference León, Montero and Nagel11, Reference León, Nagel, Ohser and Arscott12]. Code for simulation of those tessellations is available in [Reference León10].
Acknowledgements
The authors thank the referees, the editor, and the executive editor for reading the manuscript carefully and for very helpful comments and suggestions.
Funding information
This work was supported by the Center for Mathematical Modeling ANID Basal FB210005. In particular, Werner Nagel is indebted for the support of his visits at the Center, where this paper was finished in March 2023.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.