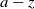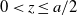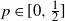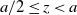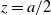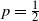Stochastic ordering results on the duration of the gambler’s ruin game

Abstract

In the classical gambler’s ruin problem, the gambler plays an adversary with initial capitals z and $a-z$, respectively, where $a>0$ and $0< z < a$ are integers. At each round, the gambler wins or loses a dollar with probabilities p and $1-p$. The game continues until one of the two players is ruined. For even a and $0<z\leq {a}/{2}$, the family of distributions of the duration (total number of rounds) of the game indexed by $p \in [0,{\frac{1}{2}}]$ is shown to have monotone (increasing) likelihood ratio, while for ${a}/{2} \leq z<a$, the family of distributions of the duration indexed by $p \in [{\frac{1}{2}}, 1]$ has monotone (decreasing) likelihood ratio. In particular, for $z={a}/{2}$, in terms of the likelihood ratio order, the distribution of the duration is maximized over $p \in [0,1]$ by $p={\frac{1}{2}}$. The case of odd a is also considered in terms of the usual stochastic order. Furthermore, as a limit, the first exit time of Brownian motion is briefly discussed.

1. Introduction and main results

In [4, Chapter XIV], the classical gambler’s ruin problem is studied in detail, in which the gambler plays an adversary with initial capitals z and $a-z$ , respectively, where $a>0$ and $0\le z \le a$ are integers. At each round, the gambler wins or loses a dollar with probabilities p and q ( $=1-p$ ). The game continues until one of the two players is ruined (and the other player’s capital reaches the maximum value a). We use the symbol ${\mathbb{P}}_{p,z,a}$ to denote the probability measure with parameters p, z, and a. The duration (total number of rounds) of the game is denoted by N, whose distribution depends on p, z, and a and is denoted by ${\mathcal{L}}_{p,z,a}(N)$ . We are concerned with stochastic ordering relations for the family of distributions $\{\mathcal{L}_{p,z,a}(N)\colon 0\le p \le 1,\, 0\le z \le a\}$ .

Letting $I=0$ if the gambler is ruined and $I=1$ otherwise, the generating function for N admits the following explicit expression [4, (4.11) and (4.12), p. 351]:

\begin{align*} \sum_{n=0}^\infty {\mathbb{P}}_{p,z,a}(N=n) s^n & = \sum_{n=0}^\infty {\mathbb{P}}_{p,z,a}(N=n, I=0) s^n+\sum_{n=0}^\infty {\mathbb{P}}_{p,z,a}(N=n, I=1) s^n, \\[5pt] \sum_{n=0}^\infty {\mathbb{P}}_{p,z,a}(N=n, I=0) s^n & = \bigg(\frac{q}{p}\bigg)^z \frac{\lambda_1^{a-z}(s)-\lambda_2^{a-z}(s)}{\lambda_1^a(s)-\lambda_2^a(s)}, \\[5pt] \sum_{n=0}^\infty {\mathbb{P}}_{p,z,a}(N=n, I=1) s^n & = \frac{\lambda_1^z(s)-\lambda_2^z(s)}{\lambda_1^a(s)-\lambda_2^a(s)},\end{align*}

where, for $0<s<1$ ,

\[ \lambda_1(s)=\frac{1+\sqrt{1-4pq s^2}}{2ps}, \qquad \lambda_2(s)=\frac{1-\sqrt{1-4pq s^2}}{2ps}.\]

Furthermore, for even $n-z$ and $n>1$ [4, (5.7) and (5.8), pp. 353--354],

(1) \begin{equation} {\mathbb{P}}_{p,z,a}(N=n, I=0) = a^{-1} 2^{n+1} p^{(n-z)/2} q^{(n+z)/2}\!\!\!\! \sum_{1 \le \nu <a/2}\!\!\!\! \cos^{n-1} \frac{\pi \nu}{a} \sin\frac{\pi \nu}{a} \sin\frac{\pi z \nu}{a},\end{equation}

and ${\mathbb{P}}_{p,z,a}(N=n, I=0)=0$ for odd $n-z$ . By symmetry, for even $n-a+z$ and $n>1$ ,

(2) \begin{equation} {\mathbb{P}}_{p,z,a}(N=n, I=1) = a^{-1} 2^{n+1} p^{(n+a-z)/2} q^{(n-a+z)/2}\!\!\!\! \sum_{1 \le \nu <a/2}\!\!\!\! \cos^{n-1} \frac{\pi \nu}{a} \sin\frac{\pi \nu}{a} \sin\frac{\pi (a-z) \nu}{a},\end{equation}

and ${\mathbb{P}}_{p,z,a}(N=n, I=1)=0$ for odd $n-a+z$ .

When a is an even integer, it is shown in [8] that $\mathcal{L}_{{1}/{2}, {a}/{2},a}(N)$ is stochastically larger than $\mathcal{L}_{p, {a}/{2},a}(N)$ for $p \neq \frac{1}{2}$ . In terms of the likelihood ratio order, which is stronger than the usual stochastic order (see, e.g., [10]), a stronger version of their result may be derived as follows. Let $X_{n,p}$ , $n=1,2,\dots$ , be independent and identically distributed (i.i.d.) with

(3) \begin{equation} \mathbb{P}(X_{n,p}=1)=p=1-\mathbb{P}(X_{n,p}=-1).\end{equation}

For $0<z<a$ and $n \ge 1$ , let

\begin{align*} {\mathcal{S}}_{z,a}^+(n) & = \{(\omega_1,\dots,\omega_n)\in \{-1,1\}^n \colon 0< z+\omega_1+\cdots+\omega_i<a, i=1,\dots, n-1,\\[5pt] & \qquad z+\omega_1+\dots+\omega_n=a\}, \\[5pt] {\mathcal{S}}_{z,a}^-(n) & = \{(\omega_1,\dots,\omega_n)\in \{-1,1\}^n \colon 0< z+\omega_1+\cdots+\omega_i<a, i=1,\dots, n-1,\\[5pt] & \qquad z+\omega_1+\dots+\omega_n=0\}.\end{align*}

For $z \in \{0,a\}$ and $n\ge 1$ , let $\mathcal{S}_{z,a}^+(n)=\mathcal{S}_{z,a}^-(n)=\emptyset$ . Note that $\mathcal{S}_{z,a}^-(n)=\emptyset$ if n and z have opposite parity, while $\mathcal{S}_{z,a}^+(n)=\emptyset$ if n and $a-z$ have opposite parity. Assume a is even and $0<z<a$ , so that z and $a-z$ are of the same parity. Then we have ${\mathbb{P}}_{p,z,a}(N=n)=0$ if n and z have opposite parity; and for $n=\min\{z,a-z\}, \min\{z,a-z\}+2,\dots$ ,

(4) \begin{align} {\mathbb{P}}_{p,z,a}(N=n) & = \mathbb{P}((X_{1,p},\dots,X_{n,p}) \in {\mathcal{S}}_{z,a}^+(n)) + \mathbb{P}((X_{1,p},\dots,X_{n,p}) \in {\mathcal{S}}_{z,a}^-(n)) \nonumber \\[5pt] & = p^{({n+a-z})/{2}} q^{({n-a+z})/{2}} |{\mathcal{S}}_{z,a}^+(n)| + p^{({n-z})/{2}} q^{({n+z})/{2}} |{\mathcal{S}}_{z,a}^-(n)| \nonumber \\[5pt] & = (pq)^{{n}/{2}}\bigg[\bigg(\frac{p}{q}\bigg)^{({a-z})/{2}} |{\mathcal{S}}_{z,a}^+(n)| + \bigg(\frac{q}{p}\bigg)^{{z}/{2}} |{\mathcal{S}}_{z,a}^-(n)|\bigg], \end{align}

where $|S|$ denotes the cardinality of the set S. For $z={a}/{2}$ , we have $|\mathcal{S}_{{{a}/{2}},a}^+(n)| = |\mathcal{S}_{{{a}/{2}},a}^-(n)|$ by symmetry, which together with (4) implies that

\begin{equation*} \mathbb{P}_{p,{{a}/{2}},a}(N=n) = (pq)^{{n}/{2}}\bigg[\bigg(\frac{p}{q}\bigg)^{{a}/{4}} + \bigg(\frac{q}{p}\bigg)^{{a}/{4}}\bigg] |\mathcal{S}_{{{a}/{2}},a}^+(n)|.\end{equation*}

So, for $p, p' \in (0,1)$ (with $q'=1-p'$ ) and $n={a}/{2}, {a}/{2}+2,\dots$ ,

\begin{equation*} \frac{\mathbb{P}_{p',{{a}/{2}},a}(N=n)}{\mathbb{P}_{p,{{a}/{2}},a}(N=n)} = \bigg(\frac{p'q'}{pq}\bigg)^{{n}/{2}} \bigg\{\bigg[\bigg(\frac{p'}{q'}\bigg)^{{a}/{4}} + \bigg(\frac{q'}{p'}\bigg)^{{a}/{4}}\bigg]\big/\bigg[\bigg(\frac{p}{q}\bigg)^{{a}/{4}} + \bigg(\frac{q}{p}\bigg)^{{a}/{4}}\bigg]\bigg\},\end{equation*}

which is increasing in n if $\big|p-{\frac{1}{2}}\big| > \big|p'-{\frac{1}{2}}\big|$ . Consequently, for even a and $z={a}/{2}$ , if p and $ p' \in [0,1]$ satisfy $\big|p-{\frac{1}{2}}\big| > \big|p'-{\frac{1}{2}}\big|$ , then $\mathcal{L}_{p',{{a}/{2}},a}(N)$ is larger than $\mathcal{L}_{p,{{a}/{2}},a}(N)$ in the likelihood ratio order. For a family of distributions indexed by $\theta \in \mathcal{I}$ (an interval) with probability mass/density functions $f_\theta(\cdot)$ on $\mathcal{X}$ (a subset of the real line), it is said to have monotone (increasing) likelihood ratio if

(5) \begin{equation} f_\theta (x) f_{\theta'} (x') \geq f_{\theta'}(x) f_{\theta}(x')\end{equation}

whenever $x,x' \in \mathcal{X}$ and $\theta, \theta' \in \mathcal{I}$ satisfy $x<x'$ and $\theta<\theta'$ , and is said to have monotone (decreasing) likelihood ratio if the inequality (5) is reversed; see [6]. Indeed, we have shown the following result.

Theorem 1. For even $a\ge 4$ and $z={a}/{2}$ , the family of distributions $\big\{\mathcal{L}_{p,{{a}/{2}},a}(N)\colon 0\le p \le {\frac{1}{2}}\big\}$ has monotone (increasing) likelihood ratio, and the family of distributions $\big\{\mathcal{L}_{p,{{a}/{2}},a}(N)\colon {\frac{1}{2}} \le p \le 1\big\}$ has monotone (decreasing) likelihood ratio.

By Theorem 1, in terms of the likelihood ratio order, the distribution $\mathcal{L}_{p, {{a}/{2}},a}(N)$ is maximized over $p \in [0,1]$ by $p={\frac{1}{2}}$ , implying the result of [8].

We next consider the more general case with a even and $z \neq {{a}/{2}}$ . We need to establish a crucial monotonicity result for $p={\frac{1}{2}}$ , which is of independent interest. For $p={\frac{1}{2}}$ , note that

\begin{equation*} {\mathbb{P}}_{p,z,a}(N=n, I=1)=2^{-n} |{\mathcal{S}}_{z,a}^+(n)|, \qquad {\mathbb{P}}_{p,z,a}(N=n, I=0)=2^{-n} |{\mathcal{S}}_{z,a}^-(n)|.\end{equation*}

Theorem 2. For $p={\frac{1}{2}}$ , even $a\ge 4$ , and $0<z<{{a}/{2}}$ , as $n \in \{z, z+2,\dots\}$ increases to $\infty$ ,

\begin{equation*} \frac{{\mathbb{P}}_{p,z,a}(N=n, I=1)}{{\mathbb{P}}_{p,z,a}(N=n)} = \frac{|{\mathcal{S}}_{z,a}^+(n)|}{|{\mathcal{S}}_{z,a}^+(n)|+|{\mathcal{S}}_{z,a}^-(n)|} \end{equation*}

monotonically increases to ${\frac{1}{2}}$ . Equivalently, for $p={\frac{1}{2}}$ and $0<z<{{a}/{2}}$ ,

$$ \frac{{\mathbb{P}}_{p,z,a}(N=n, I=1)}{{\mathbb{P}}_{p,z,a}(N=n,I=0)} = \frac{|{\mathcal{S}}_{z,a}^+(n)|}{|{\mathcal{S}}_{z,a}^-(n)|} $$

monotonically increases to 1 as $n \in \{z, z+2,\dots\}$ increases to $\infty$ .

With the help of Theorem 2, the next theorem can be readily shown, which is an extension of Theorem 1 from $z={{a}/{2}}$ to $z \neq {{a}/{2}}$ .

Theorem 3. For even $a \geq 4$ and $0<z<{{a}/{2}}$ , the family of distributions $\big\{{\mathcal{L}}_{p,z,a}(N)\colon 0\le p \le {\frac{1}{2}}\big\}$ has monotone (increasing) likelihood ratio, and for ${{a}/{2}} <z< a$ , the family of distributions $\big\{{\mathcal{L}}_{p,z,a}(N)\colon {\frac{1}{2}} \le p \le 1\big\}$ has monotone (decreasing) likelihood ratio.

For the case of odd a, analogous results do not hold unless the likelihood ratio order is replaced by a weaker stochastic order. To see this, consider odd $a\geq 3$ and $0<z<a$ . Then z and $a-z$ have opposite parity. So, for all n, either ${\mathcal{S}}_{z,a}^-(n)=\emptyset$ or ${\mathcal{S}}_{z,a}^+(n)=\emptyset$ . For even $n-z \geq 0$ ,

\begin{equation*} {\mathbb{P}}_{p,z,a}(N=n) = p^{({n-z})/{2}} q^{({n+z})/{2}} |{\mathcal{S}}_{z,a}^-(n)| = (pq)^{{n}/{2}}\bigg(\frac{q}{p}\bigg)^{{z}/{2}} |{\mathcal{S}}_{z,a}^-(n)|,\end{equation*}

while for even $n-a+z \geq 0$ ,

\begin{equation*} {\mathbb{P}}_{p,z,a}(N=n) = p^{({n+a-z})/{2}} q^{({n-a+z})/{2}} |{\mathcal{S}}_{z,a}^+(n)| = (pq)^{{n}/{2}}\bigg(\frac{p}{q}\bigg)^{({a-z})/{2}} |{\mathcal{S}}_{z,a}^+(n)|.\end{equation*}

We have

(6) \begin{equation} \frac{\mathbb{P}_{p',z,a}(N=n)}{{\mathbb{P}}_{p,z,a}(N=n)} = \begin{cases} \bigg(\dfrac{p'q'}{pq}\bigg)^{{n}/{2}}\bigg(\dfrac{p q'}{p' q}\bigg)^{{z}/{2}} & \text{for } n=z, z+2,\dots, \\[5pt] \bigg(\dfrac{p'q'}{pq}\bigg)^{{n}/{2}}\bigg(\dfrac{p'q}{pq'}\bigg)^{({a-z})/{2}} & \text{for } n=a-z,a-z+2,\dots \end{cases}\end{equation}

Consider $0<p<p'\leq {\frac{1}{2}}$ and $0<z<{\frac{a}{2}}$ . By (6), for all $n\geq a-z\ (>z)$ ,

\begin{equation*} \bigg[\frac{\mathbb{P}_{p',z,a}(N=n+2)}{{\mathbb{P}}_{p,z,a}(N=n+2)}\bigg] \big/ \bigg[\frac{\mathbb{P}_{p',z,a}(N=n)}{{\mathbb{P}}_{p,z,a}(N=n)}\bigg] = \frac{p' q'}{pq}>1,\end{equation*}

i.e. the likelihood ratio $\mathbb{P}_{p',z,a}(N=n)/{\mathbb{P}}_{p,z,a}(N=n)$ increases by a factor of $p' q'/pq$ when n increases by 2. On the other hand, by (6) again, we have, for $n=a-z,a-z+2,\dots$ ,

\begin{align*} & \bigg[\frac{\mathbb{P}_{p',z,a}(N=n+1)}{{\mathbb{P}}_{p,z,a}(N=n+1)}\bigg] \big/ \bigg[\frac{\mathbb{P}_{p',z,a}(N=n)}{{\mathbb{P}}_{p,z,a}(N=n)}\bigg] \\[5pt] & \quad = \bigg[\bigg(\frac{p'q'}{pq}\bigg)^{({n+1})/{2}}\bigg(\frac{p q'}{p' q}\bigg)^{{z}/{2}}\bigg] \big/ \bigg[\bigg(\frac{p'q'}{pq}\bigg)^{{n}/{2}}\bigg(\frac{p'q}{pq'}\bigg)^{({a-z})/{2}}\bigg] \\[5pt] & \quad = \bigg(\frac{p}{p'}\bigg)^{({a-1})/{2}}\bigg(\frac{q'}{q}\bigg)^{({a+1})/{2}}< 1,\end{align*}

showing that the likelihood ratio $\mathbb{P}_{p',z,a}(N=n)/{\mathbb{P}}_{p,z,a}(N=n)$ is not monotonically increasing in n. The next theorem gives stochastic ordering results for the odd a case in terms of the usual stochastic order.

Theorem 4. Let $a\geq 3$ be an odd integer. For $0<z<{{a}/{2}}$ and $0\leq p<p' \leq {\frac{1}{2}}$ , ${\mathcal{L}}_{p,z,a}(N)$ is stochastically smaller than $\mathcal{L}_{p',z,a}(N)$ , and for ${{a}/{2}}<z<a$ and ${\frac{1}{2}} \leq p<p' \leq 1$ , ${\mathcal{L}}_{p,z,a}(N)$ is stochastically larger than $\mathcal{L}_{p',z,a}(N)$ .

The long and technical proof of Theorem 2 is given in Section 2, while Sections 3 and 4 present the proofs of Theorems 3 and 4, respectively. We close this section with a number of remarks on some implications of the above results and a conjecture for odd a related to the work of [8].

Remark 1. For $p={\frac{1}{2}}$ , the conditional distributions of N given $I=0$ and $I=1$ , denoted by $\mathcal{L}_{{{1}/{2}}, z,a}(N \mid I=0)$ and $\mathcal{L}_{{{1}/{2}}, z,a}(N \mid I=1)$ , have respective probability mass functions

\begin{alignat*}{2} \mathbb{P}_{{{1}/{2}},z,a}(N=n \mid I=0) & = \bigg(\frac{a}{a-z}\bigg) \mathbb{P}_{{{1}/{2}},z,a}(N=n, I=0), \quad & & n=z, z+2, \dots, \\[5pt] \mathbb{P}_{{{1}/{2}},z,a}(N=n \mid I=1) & = \bigg(\frac{a}{z}\bigg) \mathbb{P}_{{{1}/{2}},z,a}(N=n, I=1), & & n=a-z, a-z+2, \dots \end{alignat*}

So, for even a and $0<z<{{a}/{2}}$ , Theorem 2 is equivalent to saying that $\mathcal{L}_{{{1}/{2}}, z,a}(N \mid I=1)$ is larger than $\mathcal{L}_{{{1}/{2}}, z,a}(N \mid I=0)$ in the likelihood ratio order.

Remark 2. For even a, Theorem 3 does not cover the case ${{a}/{2}}<z<a$ and $p\le {\frac{1}{2}}$ . In fact, for ${{a}/{2}} <z<a$ and $0<p<p'\leq {\frac{1}{2}}$ , ${\mathcal{L}}_{p,z,a}(N)$ is neither stochastically smaller nor stochastically larger than $\mathbb{L}_{p',z,a}(N)$ . To see this, note that

\begin{align*} {\mathbb{P}}_{p,z,a}(N \leq a-z) &= {\mathbb{P}}_{p,z,a}(N=a-z) = p^{a-z} < (p')^{a-z}=\mathbb{P}_{p',z,a}(N=a-z)\\[5pt] &= \mathbb{P}_{p',z,a}(N \leq a-z). \end{align*}

On the other hand, ${\mathbb{P}}_{p,z,a}(N \leq n)> \mathbb{P}_{p',z,a}(N \leq n)$ for large n, as shown below. Since $|{\mathcal{S}}_{z,a}^+(n)|=|\mathcal{S}^-_{a-z,a}(n)|$ and $|{\mathcal{S}}_{z,a}^-(n)|=|\mathcal{S}^+_{a-z,a}(n)|$ , it follows from Theorem 2 that $|{\mathcal{S}}_{z,a}^-(n)|/|{\mathcal{S}}_{z,a}^+(n)|=|\mathcal{S}^+_{a-z,a}(n)|/|\mathcal{S}^-_{a-z,a}(n)|$ increases to 1 as $n\in \{z,z+2,\dots\}$ increases to $\infty$ . By (4), as $n \in \{z,z+2,\dots\}$ increases to $\infty$ ,

(7) \begin{equation} \bigg(\frac{pq}{p'q'}\bigg)^{{n}/{2}}\bigg(\frac{\mathbb{P}_{p',z,a}(N=n)}{{\mathbb{P}}_{p,z,a}(N=n)}\bigg) \longrightarrow \frac{({p'}/{q'})^{({a-z})/{2}} + ({q'}/{p'})^{{z}/{2}}}{({p}/{q})^{({a-z})/{2}} + ({q}/{p})^{{z}/{2}}}. \end{equation}

Since $pq<p'q'$ , we have $\lim_{n \to \infty} {\mathbb{P}}_{p,z,a}(N \geq n)/\mathbb{P}_{p',z,a}(N \geq n)=0$ by (7). So ${\mathbb{P}}_{p,z,a}(N \leq n)> \mathbb{P}_{p',z,a}(N \leq n)$ for large n.

Remark 3. In view of (6) and (7), it can be shown that for $0<z<a$ and $p, p' \in (0,1)$ ,

\begin{equation*} \lim_{n \to \infty} \frac{1}{n} \log \bigg(\frac{\mathbb{P}_{p',z,a}(N\geq n)} {{\mathbb{P}}_{p,z,a}(N \geq n)}\bigg) = {\frac{1}{2}} \log \bigg(\frac{p' q'}{pq}\bigg). \end{equation*}

Thus, ${\mathcal{L}}_{p,z,a}(N)$ has much lighter tails than $\mathcal{L}_{p',z,a}(N)$ for $\big|p-{\frac{1}{2}}\big| > \big|p'-{\frac{1}{2}}\big|$ .

Remark 4. For even a and $z={{a}/{2}}$ , it is shown in [8] that the distribution ${\mathcal{L}}_{p,z,a}(N)$ is stochastically maximized over $p \in [0,1]$ by $p={\frac{1}{2}}$ . Can an analogous result hold for odd a? For odd a, it seems natural to consider a random initial state z that takes on the two middle values $({a+1})/{2}$ and $({a-1})/{2}$ with equal probabilities. Then the distribution of the duration N is a mixture of the two distributions $\mathcal{L}_{p,({a+1})/{2},a}(N)$ and $\mathcal{L}_{p,({a-1})/{2},a}(N)$ with equal weights, denoted by ${\frac{1}{2}}\mathcal{L}_{p,({a+1})/{2},a}(N) + {\frac{1}{2}}\mathcal{L}_{p,({a-1})/{2},a}(N)$ . Note that for $p={\frac{1}{2}}$ , $\mathcal{L}_{{{1}/{2}},({a+1})/{2},a}(N)=\mathcal{L}_{{{1}/{2}},({a-1})/{2},a}(N)$ , and for $p+p'=1$ ,

\[ {\frac{1}{2}}\mathcal{L}_{p,({a+1})/{2},a}(N) + {\frac{1}{2}}\mathcal{L}_{p,({a-1})/{2},a}(N) = {\frac{1}{2}}\mathcal{L}_{p',({a+1})/{2},a}(N) + {\frac{1}{2}}\mathcal{L}_{p',({a-1})/{2},a}(N). \]

We conjecture that ${\frac{1}{2}}\mathcal{L}_{p,({a+1})/{2},a}(N) + {\frac{1}{2}}\mathcal{L}_{p,({a-1})/{2},a}(N)$ is stochastically maximized over $p \in [0,1]$ by $p={\frac{1}{2}}$ , which can be shown to hold for small odd a. Moreover, this conjecture is equivalent to saying that ${\frac{1}{2}}{\mathbb{P}}_{p,(a+1)/2,a}(N \geq n) + {\frac{1}{2}}{\mathbb{P}}_{p,(a-1)/2,a}(N \geq n)$ is maximized over $p \in [0,1]$ by $p={\frac{1}{2}}$ for all n. It may be verified directly for small n.

Remark 5. [5, II.7] introduces a model of randomized random walks where instead of successive jumps occurring at epochs $1,2,\dots$ , the time intervals between successive jumps are assumed to be i.i.d. exponential random variables with mean 1. This model is a compound Poisson process $Z_t=\sum_{n=1}^{\Pi_t} X_{n,p}$ , $t\geq 0$ , where $X_{n,p}$ ( $n=1,2,\dots$ ) are i.i.d. as defined in (3), and $\Pi_t$ is a Poisson process of constant rate 1 (independent of the $X_{n,p}$ ). (For a discussion of compound Poisson processes, see, e.g., [7, 16.9].) For $0<z<a$ , let $\mathcal{T}\;:\!=\;\inf\{t>0\colon z+Z_t \notin (0,a)\}$ , the first exit time of the process $z+Z_t$ from the interval (0,a). We denote the distribution of $\mathcal{T}$ by $\mathcal{L}_{p,z,a}(\mathcal{T})$ , which is the same as the distribution of $\sum_{i=1}^N \mathcal{E}_i$ where N is the duration of the gambler’s ruin game and $\mathcal{E}_i$ ( $i=1,2,\dots$ ) are i.i.d. exponential with mean 1 (independent of N). We write $\mathcal{L}_{p,z,a}(\mathcal{T}) = \mathcal{L}_{p,z,a}\big(\sum_{i=1}^N \mathcal{E}_i\big)$ . In view of this, if ${\mathcal{L}}_{p,z,a}(N)$ is stochastically smaller than $\mathcal{L}_{p',z,a}(N)$ , then $\mathcal{L}_{p,z,a}(\mathcal{T})$ is stochastically smaller than $\mathcal{L}_{p',z,a}(\mathcal{T})$ . In other words, the usual stochastic order relation concerning the distribution of N carries over to $\mathcal{T}$ . However, the likelihood ratio order relation does not carry over. It follows from Theorems 3 and 4 that, for $0<p<p'\le {\frac{1}{2}}$ and $0<z\leq {{a}/{2}}$ , $\mathcal{L}_{p,z,a}(\mathcal{T})$ is stochastically smaller than $\mathcal{L}_{p',z,a}(\mathcal{T})$ .

Remark 6. [4, XIV.6] discusses the connection of the gambler’s ruin game with Brownian motion as a limit, which is briefly described below. To have Brownian motion as a limit, the time and step size for the random walk in the gambler’s ruin problem may be rescaled such that there are r steps per unit time and each step causes a displacement equal to $\pm \delta$ . Given real values c and $0<\xi<\alpha$ , let

(8) \begin{equation} \delta \to 0, \quad r \to \infty, \quad p \to {\frac{1}{2}}, \quad z \to \infty, \quad a \to \infty \end{equation}

in such a way that

(9) \begin{equation} (p-q)\delta r \to c, \quad 4pq \delta^2 r \to 1, \quad z \delta \to \xi, \quad a \delta \to \alpha. \end{equation}

Then the duration N of the gambler’s ruin game with initial state z becomes, in the limit, the first exit time $\tau\;:\!=\;\inf\{t>0\colon \xi+ct+B_t \notin (0,\alpha)\}$ from the interval $(0,\alpha)$ , where $B_t$ is standard Brownian motion and $\xi+ct+B_t$ is Brownian motion with drift parameter c and initial state $\xi$ . Denote the density function of $\tau$ by $u_{c,\xi,\alpha}(t)$ , which may be decomposed as $u_{c,\xi,\alpha}(t)=u_{c,\xi,\alpha}^-(t)+u_{c,\xi,\alpha}^+(t)$ . Here, $u_{c,\xi,\alpha}^-(t)$ and $u_{c,\xi,\alpha}^+(t)$ denote, respectively, the density functions of $\tau$ when the Brownian motion process exits through the lower and upper boundaries, i.e., for $t>0$ ,

\begin{align*} \mathbb{P}(\tau \leq t,\, \xi+c \tau+B_\tau=0) & = \int_0^t u_{c,\xi,\alpha}^-(s)\,{\mathrm{d}} s, \\[5pt] \mathbb{P}(\tau \leq t,\, \xi+c \tau+B_\tau=\alpha) & = \int_0^t u_{c,\xi,\alpha}^+(s)\,{\mathrm{d}} s. \end{align*}

Since $u_{c,\xi,\alpha}^-(t)$ and $u_{c,\xi,\alpha}^+(t)$ are the continuous-time counterparts of ${\mathbb{P}}_{p,z,a}(N=n,I=0)$ and ${\mathbb{P}}_{p,z,a}(N=n,I=1)$ as given in (1) and (2), applying a standard limiting argument to (1) and (2) yields

(10) \begin{align} u_{c,\xi,\alpha}^-(t) = \pi\alpha^{-2}{\mathrm{e}}^{-c(ct+2\xi)/2}\sum_{\nu=1}^\infty\nu{\mathrm{e}}^{-\nu^2\pi^2t/2\alpha^2} \sin\frac{\pi \xi \nu}{\alpha}, \end{align}

(11) \begin{align} u_{c,\xi,\alpha}^+(t) = \pi\alpha^{-2}{\mathrm{e}}^{c(-ct+2\alpha-2\xi)/2}\sum_{\nu=1}^\infty\nu{\mathrm{e}}^{-\nu^2\pi^2t/2\alpha^2} \sin\frac{\pi (\alpha-\xi) \nu}{\alpha}, \end{align}

where (10) is [4, (6.15) (with $D=1$ ), p. 359] and (11) is due to $u_{c,\xi,\alpha}^+(t)=u_{-c,\alpha-\xi,\alpha}^-(t)$ by symmetry. In [4, Problem 22, p. 370], (10) and (11) are given in the following alternative form:

(12) \begin{align} u_{c,\xi,\alpha}^-(t) & = \frac{1}{\sqrt{2\pi t^3}\,}{\mathrm{e}}^{-c(ct+2\xi)/2}\sum_{k=-\infty}^{\infty} (\xi+2k\alpha){\mathrm{e}}^{-(\xi+2 k \alpha)^2/{2t}}, \end{align}

(13) \begin{align} u_{c,\xi,\alpha}^+(t) & = \frac{1}{\sqrt{2 \pi t^3}\,}{\mathrm{e}}^{c(-ct+2\alpha-2\xi)/2}\sum_{k=-\infty}^{\infty} (\alpha-\xi+2k\alpha){\mathrm{e}}^{-(\alpha-\xi+2k\alpha)^2/{2t}}. \end{align}

(See also [3] for the Laplace transforms of $u_{c,\xi,\alpha}^-(t)$ and $u_{c,\xi,\alpha}^+(t)$ .) Since a can be taken to be an even number as a increases to $\infty$ in (8) and (9), the monotonicity property of ${\mathbb{P}}_{p,z,a}(N=n,I=1)/{\mathbb{P}}_{p,z,a}(N=n,I=0)$ with $p={\frac{1}{2}}$ and $0<z<{{a}/{2}}$ in Theorem 2 carries over to the continuous-time counterpart $u_{c,\xi,\alpha}^+(t)/u_{c,\xi,\alpha}^-(t)$ with $c=0$ and $0<\xi<{\alpha}/{2}$ . Moreover, in (10) and (11), the term with $\nu=1$ is dominant for large t, so that $\lim_{t \to \infty} u_{0,\xi,\alpha}^+(t)/u_{0,\xi,\alpha}^-(t)=1$ . On the other hand, in (12) and (13), the term with $k=0$ is dominant for small t, so that $\lim_{t \to 0+} u_{0,\xi,\alpha}^+(t)/u_{0,\xi,\alpha}^-(t)=0$ for $0<\xi < {\alpha}/{2}$ . Hence, for $0<\xi<{\alpha}/{2}$ , as t increases from 0 to $\infty$ , $u_{0,\xi,\alpha}^+(t)/u_{0,\xi,\alpha}^-(t)$ monotonically increases from 0 to 1. (Equivalently, for $c=0$ and $0<\xi<{\alpha}/{2}$ , the conditional distribution of $\tau$ given $\xi +B_{\tau}=0$ (which has probability density $({\alpha}/({\alpha-\xi})) u_{0,\xi,\alpha}^-(t)$ ) is smaller, in the likelihood ratio order, than the conditional distribution of $\tau$ given $\xi+B_{\tau}=\alpha$ (which has probability density $({\alpha}/{\xi}) u_{0,\xi,\alpha}^+(t)$ ).) Furthermore, the monotone likelihood ratio property for N in Theorem 3 also carries over to $\tau$ . Specifically, for $0<\xi\leq {\alpha}/{2}$ , the family of distributions $\{\mathcal{L}_{c,\xi,\alpha}(\tau)\colon c \in (\!-\!\infty, 0]\}$ has monotone (increasing) likelihood ratio, while for ${\alpha}/{2}\leq \xi <\alpha$ , the family of distributions $\{\mathcal{L}_{c,\xi,\alpha}(\tau)\colon c \in [0,\infty)\}$ has monotone (decreasing) likelihood ratio. In particular, in terms of the likelihood ratio order, the distribution $\mathcal{L}_{c,{\alpha}/{2},\alpha}(\tau)$ is maximized over $c \in (\!-\!\infty, \infty)$ by $c=0$ . The first exit time $\tau$ of Brownian motion is a special case of the two-sided barrier problem in the subject of level-crossing problems for random processes. It is one of a limited number of cases where an explicit solution is available. See the survey articles [1, 2] for discussion of the related literature.

2. Proof of Theorem 2

To prove Theorem 2, we need to introduce some notation and establish a few lemmas. Let $a \ge 4$ be an even integer. For $ 0\le z \le a$ and $n\ge 1$ , let $T_{z,a}^+(n)\;:\!=\;|{\mathcal{S}}_{z,a}^+(n)|$ and $T_{z,a}^-(n)\;:\!=\;|{\mathcal{S}}_{z,a}^-(n)|$ . For $n \ge 2$ and $0<z<a$ , since

\begin{equation*} {\mathcal{S}}_{z,a}^+(n) = [{\mathcal{S}}_{z,a}^+(n) \cap (\{-1\}\times \{-1,1\}^{n-1})] \cup [{\mathcal{S}}_{z,a}^+(n) \cap (\{1\} \times \{-1,1\}^{n-1})],\end{equation*}

we have

(14) \begin{equation} T_{z,a}^+(n) = |{\mathcal{S}}_{z,a}^+(n)| = |\mathcal{S}_{z-1,a}^+(n-1)| + |\mathcal{S}_{z+1,a}^+(n-1)| = T_{z-1,a}^+(n-1) + T_{z+1,a}^+(n-1).\end{equation}

Let $T_{z,a}^+(0)=1$ or 0 according as $z=a$ or $0\le z<a$ . Then (14) also holds for $n=1$ and $0<z<a$ . That is,

(15) \begin{equation} T_{z,a}^+(n) = T_{z-1,a}^+(n-1) + T_{z+1,a}^+(n-1)\qquad\mathrm{for}\ n\ge 1\ \mathrm{and}\ 0<z<a.\end{equation}

Similarly,

(16) \begin{equation} T_{z,a}^-(n) = T_{z-1,a}^-(n-1) + T_{z+1,a}^-(n-1)\qquad\mathrm{for}\ n\ge 1\ \mathrm{and}\ 0<z<a,\end{equation}

where $T_{z,a}^-(0)=1$ or 0 according as $z=0$ or $0<z\le a$ . Let $T_{z,a}(n)=T_{z,a}^+(n)+T_{z,a}^-(n)$ for $n\ge 0$ and $0\le z \le a$ . By (15) and (16), we have

(17) \begin{equation} T_{z,a}(n) = T_{z-1,a}(n-1) + T_{z+1,a}(n-1)\qquad\mathrm{for}\ n\ge 1\ \mathrm{and}\ 0<z<a.\end{equation}

Applying (15) twice yields

(18) \begin{align} T_{z,a}^+(n) & = T_{z-1,a}^+(n-1) + T_{z+1,a}^+(n-1) \notag \\[5pt] & = T_{z-2,a}^+(n-2)+2 T_{z,a}^+(n-2)+T_{z+2,a}^+(n-2) \quad \mathrm{for}\ n\ge 2\ \mathrm{and}\ 2\le z \le a-2.\end{align}

Similarly,

(19) \begin{equation} T_{z,a}(n) = T_{z-2,a}(n-2) + 2T_{z,a}(n-2) + T_{z+2,a}(n-2)\quad \mathrm{for}\ n\ge 2\ \mathrm{and}\ 2\le z \le a-2.\end{equation}

We have, by symmetry,

(20) \begin{align} T_{z,a}(n)=T_{z',a}(n)\qquad\text{for}\ z+z'=a.\end{align}

Below we adopt the convention that ${0}/{0}\;:\!=\;0$ and ${c}/{0}\;:\!=\;\infty$ for $c>0$ .

We are now ready to state and prove four lemmas. In particular, the inequality (21) given in Lemma 1 is a key observation for the proof of Theorem 2.

Lemma 1. For even $a \ge 6$ and $2\le z \le {{a}/{2}}-1$ ,

(21) \begin{equation} \frac{T_{z,a}(n)}{T_{z-2,a}(n)+T_{z+2,a}(n)} \ge \frac{T_{z+2,a}(n)}{T_{z,a}(n)+T_{z+4,a}(n)}\qquad \mathrm{for}\ n\ge 0. \end{equation}

Proof. By (20),

(22) \begin{equation} \frac{T_{{{a}/{2}}-1,a}(n)}{T_{{{a}/{2}}-3,a}(n)+T_{{{a}/{2}}+1,a}(n)} = \frac{T_{{{a}/{2}}+1,a}(n)}{T_{{{a}/{2}}-1,a}(n)+T_{{{a}/{2}}+3,a}(n)}\qquad \mathrm{for}\ n\ge 0, \end{equation}

from which it follows that (21) holds for $z={{a}/{2}}-1$ .

We now prove (21) by induction on n. Since $T_{z+2,a}(0)=T_{z+2,a}(1)=0$ for $2\le z \le {{a}/{2}}-1$ , (21) holds for $n=0$ and $n=1$ . Suppose (21) holds for $2 \le z \le {{a}/{2}}-1$ and for $n\le m$ with some $m\ge 1$ . We need to show that

(23) \begin{equation} \frac{T_{z,a}(m+1)}{T_{z-2,a}(m+1)+T_{z+2,a}(m+1)} \ge \frac{T_{z+2,a}(m+1)}{T_{z,a}(m+1)+T_{z+4,a}(m+1)} \end{equation}

for $2\le z \le {{a}/{2}}-1$ . By (22), (23) holds for $z={{a}/{2}}-1$ . By (17), for $3\le z \le {{a}/{2}}-2$ , (23) is equivalent to

(24) \begin{multline} \frac{T_{z-1,a}(m)+T_{z+1,a}(m)}{T_{z-3,a}(m)+T_{z-1,a}(m)+T_{z+1,a}(m)+T_{z+3,a}(m)} \\[5pt] \ge \frac{T_{z+1,a}(m)+T_{z+3,a}(m)}{T_{z-1,a}(m)+T_{z+1,a}(m)+T_{z+3,a}(m)+T_{z+5,a}(m)}. \end{multline}

For $3 \le z \le {{a}/{2}}-2$ , we have, by the induction hypothesis,

(25) \begin{align} \frac{T_{z-1,a}(m)}{T_{z-3,a}(m)+T_{z+1,a}(m)} & \ge \frac{T_{z+1,a}(m)}{T_{z-1,a}(m)+T_{z+3,a}(m)}, \end{align}

(26) \begin{align} \frac{T_{z+1,a}(m)}{T_{z-1,a}(m)+T_{z+3,a}(m)} & \ge \frac{T_{z+3,a}(m)}{T_{z+1,a}(m)+T_{z+5,a}(m)}. \end{align}

Note that the right-hand side of (25) and the left-hand side of (26) are the same. Since for $c_i, c_i'\ge 0$ $(i=1,2)$ , ${c_1}/{c_2} \ge {c'_{\!\!1}}/{c'_{\!\!2}}$ implies

\[ \frac{c_1}{c_2} \ge \frac{c_1+c'_{\!\!1}}{c_2+c'_{\!\!2}} \ge \frac{c'_{\!\!1}}{c'_{\!\!2}}, \]

it follows from (25) and (26) that the left-hand side of (24) is greater than or equal to the right-hand side of (25) while the right-hand side of (24) is less than or equal to the left-hand side of (26). This establishes (24) (and hence (23)) for $3 \le z \le {{a}/{2}}-2$ .

It remains to prove (23) for $z=2$ ; i.e.,

(27) \begin{equation} \frac{T_{2,a}(m+1)}{T_{0,a}(m+1)+T_{4,a}(m+1)} \ge \frac{T_{4,a}(m+1)}{T_{2,a}(m+1)+T_{6,a}(m+1)}. \end{equation}

Note that $T_{0,a}(m+1)=0$ and that, for $a=6$ , (27) is an equality (since $T_{2,6}(m+1)=T_{4,6}(m+1)$ and $T_{6,6}(m+1)=0$ ). By (19), for (even) $a \ge 8$ , (27) is equivalent to

(28) \begin{multline} \frac{T_{0,a}(m-1)+2 T_{2,a}(m-1)+T_{4,a}(m-1)}{T_{2,a}(m-1)+2 T_{4,a}(m-1)+T_{6,a}(m-1)} \\[5pt] \ge \frac{T_{2,a}(m-1)+2 T_{4,a}(m-1)+T_{6,a}(m-1)}{T_{0,a}(m-1)+2 T_{2,a}(m-1)+2 T_{4,a}(m-1) + 2 T_{6,a}(m-1)+T_{8,a}(m-1)}. \end{multline}

Since $T_{2,a}(m-1)=T_{4,a}(m-1)=T_{6,a}(m-1)=0$ for $m=1$ and $a \ge 8$ , (28) holds for $m=1$ . We now assume $m>1$ (implying that $T_{0,a}(m-1)=T_{a,a}(m-1)=0$ ). By (20), for $a=8$ , (28) reduces to

(29) \begin{equation} \frac{2 T_{2,8}(m-1)+T_{4,8}(m-1)}{2 T_{2,8}(m-1)+2 T_{4,8}(m-1)} \ge \frac{ T_{2,8}(m-1)+ T_{4,8}(m-1)}{ 2T_{2,8}(m-1)+ T_{4,8}(m-1)}. \end{equation}

The induction hypothesis applied to $a=8$ and $z=2$ yields

\begin{equation*} \frac{T_{2,8}(m-1)}{T_{4,8}(m-1)}=\frac{T_{2,8}(m-1)}{T_{0,8}(m-1)+T_{4,8}(m-1)} \ge \frac{T_{4,8}(m-1)}{T_{2,8}(m-1)+T_{6,8}(m-1)} =\frac{T_{4,8}(m-1)}{2 T_{2,8}(m-1)}, \end{equation*}

which implies (or more precisely, is equivalent to) (29). To show (28) for (even) $a\ge 10$ , by the induction hypothesis applied to $a\ge 10$ and $z=2,4$ ( $\le {{a}/{2}}-1$ ), we have $A_1\ge A_2 \ge A_3$ , where

\begin{equation*} A_k= \frac{T_{2k,a}(m-1)}{T_{2k-2,a}(m-1)+T_{2k+2,a}(m-1)} \qquad \mathrm{for}\ k=1,2,3. \end{equation*}

Note that

$$A_1=\frac{T_{2,a}(m-1)}{T_{0,a}(m-1)+T_{4,a}(m-1)}=\frac{T_{2,a}(m-1)}{T_{4,a}(m-1)}.$$

If $T_{2,a}(m-1)=0$ , then necessarily $m-1$ ( $\geq 1$ ) is odd and $T_{4,a}(m-1)=T_{6,a}(m-1)=T_{8,a}(m-1)=0$ , so that (28) holds trivially. Suppose $T_{2,a}(m-1)>0$ . Then each of the two sides of (28) is a weighted average of $A_1$ , $A_2$ , and $A_3$ . Indeed, the left-hand side of (28) equals $c_1 A_1 +c_2 A_2$ with weights

\begin{align*} c_1&=\frac{2T_{4,a}(m-1)}{T_{2,a}(m-1)+2T_{4,a}(m-1)+T_{6,a}(m-1)},\\[5pt] c_2&=\frac{T_{2,a}(m-1)+T_{6,a}(m-1)}{T_{2,a}(m-1)+2T_{4,a}(m-1)+T_{6,a}(m-1)}, \end{align*}

while the right-hand side of (28) equals $c'_{\!\!1} A_1+c'_{\!\!2} A_2 +c'_{\!\!3} A_3$ with weights

\begin{align*} c'_{\!\!1}&=\frac{T_{4,a}(m-1)}{2T_{2,a}(m-1)+2T_{4,a}(m-1)+2T_{6,a}(m-1)+T_{8,a}(m-1)},\\[5pt] c'_{\!\!2}&=\frac{2T_{2,a}(m-1)+2T_{6,a}(m-1)}{2T_{2,a}(m-1)+2T_{4,a}(m-1)+2T_{6,a}(m-1)+T_{8,a}(m-1)},\\[5pt] c'_{\!\!3}&=\frac{T_{4,a}(m-1)+T_{8,a}(m-1)}{2T_{2,a}(m-1)+2T_{4,a}(m-1)+2T_{6,a}(m-1)+T_{8,a}(m-1)}. \end{align*}

Since $c_1 \ge c'_{\!\!1}$ , it follows from $A_1\ge A_2 \ge A_3$ that $c_1 A_1+c_2 A_2 \ge c'_{\!\!1} A_1 +c'_{\!\!2} A_2 +c'_{\!\!3} A_3$ . This shows (28) for $a \ge 10$ and completes the induction proof.

Remark 7. The proof of Lemma 1 makes use of the induction method on n with the help of the recursion (17), which is related to first-step analysis in Markov chains (see, e.g., [9]). After the first step, the initial state z moves either down to $z-1$ or up to $z+1$ . To apply the induction hypothesis, it is necessary to consider the boundary cases $z=2$ and $z={{a}/{2}}-1$ separately from $3 \leq z \leq {{a}/{2}}-2$ . (The induction hypothesis is applicable neither in the case that $z=2$ moves down to 1 nor in the case that $z={{a}/{2}}-1$ moves up to ${{a}/{2}}$ .) The proofs of Lemmas 2 and 3 and Theorem 2 also make use of the recursions (15), (18), and (19). Again, the boundary cases need to be treated separately.

Lemma 2. For even $n\ge 2$ , ${T_{z,a}^+(n)}/{T_{z,a}(n)}$ is increasing in $z \in \{2,4,\dots, a-2\}$ . For odd $n\ge 1$ , ${T_{z,a}^+(n)}/{T_{z,a}(n)}$ is increasing in $z \in \{1,3,\dots, a-1\}$ .

Proof. Let $\rho(n)=1$ or 2 according as n is odd or even. We show that, for $n \ge 1$ , ${T_{z,a}^+(n)}/{T_{z,a}(n)}$ is increasing in $z \in \{\rho(n),\rho(n)+2,\dots, a-\rho(n)\}$ ; i.e., for $n\ge 1$ ,

(30) \begin{equation} \frac{T_{z+2,a}^+(n)}{T_{z+2,a}(n)}\ge \frac{T_{z,a}^+(n)}{T_{z,a}(n)} \qquad \text{for } z=\rho(n),\rho(n)+2,\dots, a-\rho(n)-2. \end{equation}

We proceed by induction on n. Since ${T_{z,a}^+(1)}/{T_{z,a}(1)}=0$ for $z<a-1$ , and ${T_{a-1,a}^+(1)}/{T_{a-1,a}(1)}=1$ , (30) holds for $n=1$ . Suppose (30) holds for $n \le m$ with some $m\ge 1$ . We need to show that

(31) \begin{equation} \frac{T_{z+2,a}^+(m+1)}{T_{z+2,a}(m+1)}\ge \frac{T_{z,a}^+(m+1)}{T_{z,a}(m+1)} \qquad \text{for } z=\rho(m+1),\rho(m+1)+2,\dots, a-\rho(m+1)-2. \end{equation}

Consider the case that m is even. Then $m\ge 2$ and $\rho(m+1)=1$ . For $z=1,3,\dots,a-3$ , we have, by (15) and (17),

(32) \begin{align} \frac{T_{z,a}^+(m+1)}{T_{z,a}(m+1)} =\frac{T_{z-1,a}^+(m)+T_{z+1,a}^+(m)}{T_{z-1,a}(m)+T_{z+1,a}(m)}, \end{align}

(33) \begin{align} \frac{T_{z+2,a}^+(m+1)}{T_{z+2,a}(m+1)} = \frac{T_{z+1,a}^+(m)+T_{z+3,a}^+(m)}{T_{z+1,a}(m)+T_{z+3,a}(m)}. \end{align}

The right-hand side of (32) equals ${T_{z+1,a}^+(m)}/{T_{z+1,a}(m)}$ for $z=1$ and is less than or equal to ${T_{z+1,a}^+(m)}/{T_{z+1,a}(m)}$ for $z>1$ since, by the induction hypothesis, for $z=3,\dots, a-3$ ,

\begin{equation*} \frac{T_{z+1,a}^+(m)}{T_{z+1,a}(m)}\ge \frac{T_{z-1,a}^+(m)}{T_{z-1,a}(m)}. \end{equation*}

The right-hand side of (33) equals ${T_{z+1,a}^+(m)}/{T_{z+1,a}(m)}$ for $z=a-3$ and is greater than or equal to ${T_{z+1,a}^+(m)}/{T_{z+1,a}(m)}$ for $z<a-3$ since, by the induction hypothesis, for $z=1,\dots, a-5$ ,

\begin{equation*} \frac{T_{z+3,a}^+(m)}{T_{z+3,a}(m)}\ge \frac{T_{z+1,a}^+(m)}{T_{z+1,a}(m)}. \end{equation*}

This proves (31) for the case of even m. The case of odd m can be treated similarly.

Lemma 3. For even $a\ge 4$ and $n\ge 0$ ,

(34) \begin{align} \frac{T_{1,a}^+(n+2)}{T_{1,a}(n+2)} & \ge \frac{T_{1,a}^+(n)}{T_{1,a}(n)}, \end{align}

(35) \begin{align} \frac{T_{2,a}^+(n+2)}{T_{2,a}(n+2)} & \ge \frac{T_{2,a}^+(n)}{T_{2,a}(n)}. \end{align}

Proof. Note that (34) holds trivially for even n since both sides of (34) are ${0}/{0}$ for even n. We now prove (34) for odd $n\ge 1$ . By (15),

(36) \begin{equation} T_{1,a}^+(n+2)=T_{0,a}^+(n+1)+T_{2,a}^+(n+1)=T_{2,a}^+(n+1)=T_{1,a}^+(n)+T_{3,a}^+(n). \end{equation}

Similarly, by (17), $T_{1,a}(n+2)=T_{1,a}(n)+T_{3,a}(n)$ , which together with (36) implies that

\begin{equation*} \frac{T_{1,a}^+(n+2)}{T_{1,a}(n+2)} = \frac{T_{1,a}^+(n)+T_{3,a}^+(n)}{T_{1,a}(n)+T_{3,a}(n)} \ge \frac{T_{1,a}^+(n)}{T_{1,a}(n)}, \end{equation*}

where the inequality follows from ${T_{1,a}^+(n)}/{T_{1,a}(n)} \le {T_{3,a}^+(n)}/{T_{3,a}(n)}$ (by Lemma 2).

Next, to prove (35), it suffices to consider the case of even n. For $n=0$ , the right-hand side of (35) is 0, so (35) holds. For even $n\ge 2$ and $a=4$ , both sides of (35) equal ${\frac{1}{2}}$ by symmetry. For even $n\geq 2$ and $a\ge 6$ , we have, by (18) and (19),

\begin{align*} \frac{T_{2,a}^+(n+2)}{T_{2,a}(n+2)} & = \frac{T_{0,a}^+(n)+2T_{2,a}^+(n)+T_{4,a}^+(n)}{T_{0,a}(n)+2T_{2,a}(n)+T_{4,a}(n)} \\[5pt] & = \frac{2T_{2,a}^+(n)+T_{4,a}^+(n)}{2T_{2,a}(n)+T_{4,a}(n)} \ge \frac{ T_{2,a}^+(n)}{T_{2,a}(n)}, \end{align*}

where the inequality follows from ${T_{2,a}^+(n)}/{T_{2,a}(n)} \leq {T_{4,a}^+(n)}/{T_{4,a}(n)}$ (by Lemma 2). The proof is complete.

Lemma 4. Let $\alpha_1>0$ and $\alpha_i\geq \beta_i \ge 0$ , $i=1,2,3,4$ . Suppose

\begin{equation*} \frac{\beta_4}{\alpha_4} \ge \frac{\beta_1}{\alpha_1}, \qquad \frac{\beta_1+\beta_3}{\alpha_1+\alpha_3}\ge \frac{\beta_2}{\alpha_2}, \qquad \frac{\beta_2+\beta_4}{\alpha_2+\alpha_4}\ge \frac{\beta_3}{\alpha_3}, \qquad \frac{\alpha_2}{\alpha_1+\alpha_3}\ge \frac{\alpha_3}{\alpha_2+\alpha_4}. \end{equation*}

Then

\begin{equation*} \frac{\beta_1+\beta_4}{\alpha_1+\alpha_4}\ge \frac{\beta_2+\beta_3}{\alpha_2+\alpha_3}. \end{equation*}

Proof. If $\alpha_2=0$ then $\alpha_3=0$ since ${\alpha_2}/({\alpha_1+\alpha_3}) \ge {\alpha_3}/({\alpha_2+\alpha_4})$ . So

$$\frac{\beta_1+\beta_4}{\alpha_1+\alpha_4}\ge 0=\frac{\beta_2+\beta_3}{\alpha_2+\alpha_3}.$$

If $\alpha_3=0$ , then

\[ \frac{\beta_4}{\alpha_4} \ge \frac{\beta_1}{\alpha_1} = \frac{\beta_1+\beta_3}{\alpha_1+\alpha_3}\ge \frac{\beta_2}{\alpha_2}, \]

implying that

\[ \frac{\beta_1+\beta_4}{\alpha_1+\alpha_4}\ge \frac{\beta_2}{\alpha_2} = \frac{\beta_2+\beta_3}{\alpha_2+\alpha_3}. \]

Now suppose $\alpha_2>0$ and $\alpha_3>0$ . We have

\begin{align*} 0 & \leq \frac{\alpha_2\alpha_3}{\alpha_1+\alpha_3} \bigg[\frac{\beta_2+\beta_4}{\alpha_2+\alpha_4}-\frac{\beta_3}{\alpha_3}\bigg] + \alpha_2\bigg[\frac{\beta_1+\beta_3}{\alpha_1+\alpha_3}-\frac{\beta_2}{\alpha_2}\bigg] \\[5pt] & = \frac{\alpha_2(\alpha_2+\alpha_4)\beta_1+\alpha_2\alpha_3\beta_4 - (\alpha_1\alpha_2+\alpha_1\alpha_4+\alpha_3\alpha_4)\beta_2}{(\alpha_1+\alpha_3)(\alpha_2+\alpha_4)}, \\[5pt] 0 & \leq \frac{\alpha_2\alpha_3}{\alpha_2+\alpha_4} \bigg[\frac{\beta_1+\beta_3}{\alpha_1+\alpha_3}-\frac{\beta_2}{\alpha_2}\bigg] + \alpha_3\bigg[\frac{\beta_2+\beta_4}{\alpha_2+\alpha_4}-\frac{\beta_3}{\alpha_3}\bigg] \\[5pt] & = \frac{\alpha_2\alpha_3\beta_1+\alpha_3(\alpha_1+\alpha_3)\beta_4 - (\alpha_1\alpha_2+\alpha_1\alpha_4+\alpha_3\alpha_4)\beta_3}{(\alpha_1+\alpha_3)(\alpha_2+\alpha_4)}, \end{align*}

implying that

\begin{equation*} \frac{\alpha_2(\alpha_2+\alpha_4)\beta_1+\alpha_2\alpha_3\beta_4} {\alpha_1\alpha_2+\alpha_1\alpha_4+\alpha_3\alpha_4} \geq \beta_2, \qquad \frac{\alpha_2\alpha_3\beta_1+\alpha_3(\alpha_1+\alpha_3)\beta_4} {\alpha_1\alpha_2+\alpha_1\alpha_4+\alpha_3\alpha_4} \geq \beta_3. \end{equation*}

So $C \geq \beta_2+\beta_3$ , where

\begin{equation*} C\;:\!=\;\frac{\alpha_2(\alpha_2+\alpha_3+\alpha_4)\beta_1+\alpha_3(\alpha_1+\alpha_2+\alpha_3)\beta_4} {\alpha_1\alpha_2+\alpha_1\alpha_4+\alpha_3\alpha_4}. \end{equation*}

To show $({\beta_1+\beta_4})/({\alpha_1+\alpha_4}) \ge ({\beta_2+\beta_3})/({\alpha_2+\alpha_3})$ , since $C \geq \beta_2+\beta_3$ it suffices to verify that

(37) \begin{equation} C_1\;:\!=\;(\alpha_2+\alpha_3)(\beta_1+\beta_4) -(\alpha_1+\alpha_4) C\geq 0. \end{equation}

We have

\begin{align*} C_1 (\alpha_1 \alpha_2+\alpha_1 \alpha_4 +\alpha_3 \alpha_4) & = \alpha_4[\alpha_3(\alpha_1+\alpha_3)-\alpha_2(\alpha_2+\alpha_4)]\beta_1 \\[5pt] & \quad + \alpha_1[\alpha_2(\alpha_2+\alpha_4)-\alpha_1(\alpha_1+\alpha_3)] \beta_4 \\[5pt] & = [\alpha_2(\alpha_2+\alpha_4)-\alpha_3(\alpha_1+\alpha_3)](\alpha_1\beta_4-\alpha_4\beta_1) \geq 0, \end{align*}

since ${\alpha_2}/({\alpha_1+\alpha_3}) \geq {\alpha_3}/({\alpha_2+\alpha_4})$ and ${\beta_4}/{\alpha_4} \geq {\beta_1}/{\alpha_1}$ . This proves (37), and completes the proof.

Proof of Theorem 2. We claim that, for even $a\ge 4$ and $0<z<{{a}/{2}}$ ,

(38) \begin{equation} \frac{T_{z,a}^+(n+2)}{T_{z,a}(n+2)}\ge \frac{T_{z,a}^+(n)}{T_{z,a}(n)}, \qquad n\ge 0. \end{equation}

By Lemma 3, (38) holds for $z=1$ and $z=2$ . Consequently, (38) holds for $a=4$ and $a=6$ . Note also that

(39) \begin{equation} \frac{T_{{{a}/{2}},a}^+(n+2)}{T_{{{a}/{2}},a}(n+2)} \ge \frac{T_{{{a}/{2}},a}^+(n)}{T_{{{a}/{2}},a}(n)}, \qquad n\ge 0. \end{equation}

(If n and ${{a}/{2}}$ have opposite parity, both sides of (39) are ${0}/{0}=0$ . For n and ${{a}/{2}}$ of the same parity, ${T_{{{a}/{2}},a}^+(n)}/{T_{{{a}/{2}},a}(n)}=0$ or ${\frac{1}{2}}$ according as $n<{{a}/{2}}$ or $\ge {{a}/{2}}$ . This shows (39).)

We now prove (38) for $a \geq 8$ and $3 \leq z <{{a}/{2}}$ by induction on n. For $n=0$ and $n=1$ , the right-hand side of (38) equals 0 since $T_{z,a}^+(0)=T_{z,a}^+(1)=0$ for $0<z<{{a}/{2}}$ . So (38) holds for $n\le 1$ . Suppose (38) holds for $n\le m$ with some $m \ge 1$ . We need to show that

\begin{equation*} \frac{T_{z,a}^+(m+3)}{T_{z,a}(m+3)}\ge \frac{T_{z,a}^+(m+1)}{T_{z,a}(m+1)} \qquad \text{for even } a\ge 8 \text{ and } 3 \le z<{\frac{a}{2}}. \end{equation*}

By (15) and (17), this is equivalent to

(40) \begin{equation} \frac{T_{z-1,a}^+(m+2)+T_{z+1,a}^+(m+2)}{T_{z-1,a}(m+2)+T_{z+1,a}(m+2)}\ge \frac{T_{z-1,a}^+(m)+T_{z+1,a}^+(m)}{T_{z-1,a}(m)+T_{z+1,a}(m)} \end{equation}

for $a \ge 8$ and $3\le z <{{a}/{2}}$ . By (18) and (19) applied to the left-hand side of (40), (40) is equivalent to

(41) \begin{equation} \frac{T_{z-3,a}^+(m)+3T_{z-1,a}^+(m)+3T_{z+1,a}^+(m)+T_{z+3,a}^+(m)}{T_{z-3,a}(m)+3T_{z-1,a}(m)+3T_{z+1,a}(m)+T_{z+3,a}(m)}\ge \frac{T_{z-1,a}^+(m)+T_{z+1,a}^+(m)}{T_{z-1,a}(m)+T_{z+1,a}(m)} \end{equation}

for $a \ge 8$ and $3\le z <{{a}/{2}}$ . Note that (41) holds trivially if z and m are of the same parity. Suppose z and m have opposite parity. If $T_{z-1,a}(m+2)=0$ , then $m+2<z-1$ ( $<{{a}/{2}}-1$ ), so that both sides of (40) (and hence (41)) are 0.

Now suppose $T_{z-1,a}(m+2)>0$ . We first prove (41) for $z=3$ (and even m), in which case we have $T_{z-3,a}(m)=T_{z-3,a}^+(m)=0$ , so that (41) becomes

\begin{equation*} \frac{3T_{2,a}^+(m)+3T_{4,a}^+(m)+T_{6,a}^+(m)}{3T_{2,a}(m)+3T_{4,a}(m)+T_{6,a}(m)}\ge \frac{T_{2,a}^+(m)+T_{4,a}^+(m)}{T_{2,a}(m)+T_{4,a}(m)}. \end{equation*}

This inequality holds since, by Lemma 2,

\begin{equation*} \frac{T_{6,a}^+(m)}{T_{6,a}(m)}\ge \frac{T_{4,a}^+(m)}{T_{4,a}(m)}\ge \frac{T_{2,a}^+(m)}{T_{2,a}(m)}. \end{equation*}

We now prove (41) for $4\le z <{{a}/{2}}$ (in which case necessarily $a \ge 10$ ). Note that $T_{z-1,a}(m+2)>0$ implies $T_{z-3,a}(m)>0$ . By the induction hypothesis together with (39), we have

\begin{equation*} \frac{T_{z-1,a}^+(m+2)}{T_{z-1,a}(m+2)} \ge \frac{T_{z-1,a}^+(m)}{T_{z-1,a}(m)}, \qquad \frac{T_{z+1,a}^+(m+2)}{T_{z+1,a}(m+2)} \ge \frac{T_{z+1,a}^+(m)}{T_{z+1,a}(m)}. \end{equation*}

By (18) and (19) applied to the left-hand sides of each of these inequalities, we have

(42) \begin{align} \frac{T_{z-3,a}^+(m)+2T_{z-1,a}^+(m)+T_{z+1,a}^+(m)}{T_{z-3,a}(m)+2T_{z-1,a}(m)+T_{z+1,a}(m)} & \ge \frac{T_{z-1,a}^+(m)}{T_{z-1,a}(m)}, \end{align}

(43) \begin{align} \frac{T_{z-1,a}^+(m)+2T_{z+1,a}^+(m)+T_{z+3,a}^+(m)}{T_{z-1,a}(m)+2T_{z+1,a}(m)+T_{z+3,a}(m)} & \ge \frac{T_{z+1,a}^+(m)}{T_{z+1,a}(m)}. \end{align}

Noting that the left-hand side of (42) equals

\begin{equation*} c \bigg(\frac{T_{z-3,a}^+(m)+T_{z+1,a}^+(m)}{T_{z-3,a}(m)+T_{z+1,a}(m)}\bigg) + (1-c)\bigg(\frac{T_{z-1,a}^+(m)}{T_{z-1,a}(m)}\bigg), \end{equation*}

where

\begin{equation*} c=\frac{T_{z-3,a}(m)+T_{z+1,a}(m)}{T_{z-3,a}(m)+2T_{z-1,a}(m)+T_{z+1,a}(m)}>0, \end{equation*}

the inequality in (42) implies that

(44) \begin{equation} \frac{T_{z-3,a}^+(m)+T_{z+1,a}^+(m)}{T_{z-3,a}(m)+T_{z+1,a}(m)} \geq \frac{T_{z-1,a}^+(m)}{T_{z-1,a}(m)}. \end{equation}

Similarly, if $T_{z-1,a}(m)>0$ , then the inequality in (43) implies that

(45) \begin{equation} \frac{T_{z-1,a}^+(m)+T_{z+3,a}^+(m)}{T_{z-1,a}(m)+T_{z+3,a}(m)} \geq \frac{T_{z+1,a}^+(m)}{T_{z+1,a}(m)}. \end{equation}

If $T_{z-1,a}(m)=0$ , then $T_{z+1,a}(m)=T_{z+3,a}(m)=0$ (since $z-1 < z+3 \le a-(z-1)$ ), so the inequality in (45) holds trivially.

Let

\begin{alignat*}{4} \alpha_1 & = T_{z-3,a}(m), \qquad & \alpha_2 & = T_{z-1,a}(m), \qquad & \alpha_3 & = T_{z+1,a}(m), \qquad & \alpha_4 & = T_{z+3,a}(m), \\[5pt] \beta_1 & = T_{z-3,a}^+(m), & \beta_2 & = T_{z-1,a}^+(m), & \beta_3 & = T_{z+1,a}^+(m), & \beta_4 & = T_{z+3,a}^+(m). \end{alignat*}

Since $T_{z-1,a}(m+2)>0$ , we have $\alpha_1=T_{z-3,a}(m)>0$ . By (44) and (45),

\begin{equation*} \frac{\beta_1+\beta_3}{\alpha_1+\alpha_3} \ge \frac{\beta_2}{\alpha_2}, \qquad \frac{\beta_2+\beta_4}{\alpha_2+\alpha_4} \ge \frac{\beta_3}{\alpha_3}. \end{equation*}

Furthermore, by Lemma 1,

\begin{equation*} \frac{\alpha_2}{\alpha_1+\alpha_3}=\frac{T_{z-1,a}(m)}{T_{z-3,a}(m)+T_{z+1,a}(m)} \ge \frac{T_{z+1,a}(m)}{T_{z-1,a}(m)+T_{z+3,a}(m)} = \frac{\alpha_3}{\alpha_2+\alpha_4}, \end{equation*}

and by Lemma 2,

\begin{equation*} \frac{\beta_1}{\alpha_1}=\frac{T_{z-3,a}^+(m)}{T_{z-3,a}(m)} \le \frac{T_{z+3,a}^+(m)}{T_{z+3,a}(m)} = \frac{\beta_4}{\alpha_4}. \end{equation*}

It follows from Lemma 4 that

\begin{equation*} \frac{\beta_1+\beta_4}{\alpha_1+\alpha_4} \ge \frac{\beta_2+\beta_3}{\alpha_2+\alpha_3}, \end{equation*}

implying that

\begin{align*} \frac{T_{z-1,a}^+(m)+T_{z+1,a}^+(m)}{T_{z-1,a}(m)+T_{z+1,a}(m)} & = \frac{\beta_2+\beta_3}{\alpha_2+\alpha_3} \\[5pt] & \le \frac{\beta_1+3\beta_2+3\beta_3+\beta_4}{\alpha_1+3\alpha_2+3\alpha_3+\alpha_4} \\[5pt] & = \frac{T_{z-3,a}^+(m)+3T_{z-1,a}^+(m)+3T_{z+1,a}^+(m)+T_{z+3,a}^+(m)} {T_{z-3,a}(m)+3T_{z-1,a}(m)+3T_{z+1,a}(m)+T_{z+3,a}(m)}, \end{align*}

proving (41) for $4 \le z <{{a}/{2}}$ . This completes the proof of (38), which implies that

\begin{equation*} \frac{|{\mathcal{S}}_{z,a}^+(n)|}{|{\mathcal{S}}_{z,a}^+(n)|+|{\mathcal{S}}_{z,a}^-(n)|} = \frac{T_{z,a}^+(n)}{T_{z,a}(n)} \end{equation*}

is increasing as $n \in \{z,z+2,\dots\}$ increases. Finally, as $n \in \{z,z+2,\dots\}$ tends to $\infty$ , it follows from (1) and (2) (with $p={\frac{1}{2}}$ ) that

\begin{equation*} \frac{|{\mathcal{S}}_{z,a}^+(n)|}{|{\mathcal{S}}_{z,a}^-(n)|} = \frac{{\mathbb{P}}_{p,z,a}(N=n, I=1)}{{\mathbb{P}}_{p,z,a}(N=n, I=0)} = \frac{\sum_{1 \le \nu <a/2}\cos^{n-1}({\pi\nu}/{a})\sin({\pi\nu}/{a})\sin({\pi(a-z)\nu}/{a})} {\sum_{1 \le \nu <a/2}\cos^{n-1}({\pi\nu}/{a})\sin({\pi\nu}/{a})\sin({\pi z\nu}/{a})} \end{equation*}

approaches 1, implying that ${|{\mathcal{S}}_{z,a}^+(n)|}/({|{\mathcal{S}}_{z,a}^+(n)|+|{\mathcal{S}}_{z,a}^-(n)|})$ increases to ${\frac{1}{2}}$ in the limit. The proof of Theorem 2 is complete.

3. Proof of Theorem 3

Theorem 2 plays a key role in the following proof of Theorem 3.

Proof of Theorem 3. By (4), for $0<z<{{a}/{2}}$ and $n=z,z+2,\dots$ ,

\begin{align*} {\mathbb{P}}_{p,z,a}(N=n) & = (pq)^{{n}/{2}}\bigg[\bigg(\frac{p}{q}\bigg)^{({a-z})/{2}}|{\mathcal{S}}_{z,a}^+(n)| + \bigg(\frac{q}{p}\bigg)^{{z}/{2}}|{\mathcal{S}}_{z,a}^-(n)|\bigg] \\[5pt] & = (pq)^{{n}/{2}}\bigg[\bigg(\frac{p}{q}\bigg)^{({a-z})/{2}}\frac{T_{z,a}^+(n)}{T_{z,a}(n)} + \bigg(\frac{q}{p}\bigg)^{{z}/{2}}\bigg(1-\frac{T_{z,a}^+(n)}{T_{z,a}(n)}\bigg)\bigg] T_{z,a}(n) \\[5pt] & = (pq)^{{n}/{2}}\bigg\{\bigg[\bigg(\frac{p}{q}\bigg)^{({a-z})/{2}} - \bigg(\frac{q}{p}\bigg)^{{z}/{2}}\bigg] \frac{T_{z,a}^+(n)}{T_{z,a}(n)} + \bigg(\frac{q}{p}\bigg)^{{z}/{2}}\bigg\} T_{z,a}(n). \end{align*}

So, for $0<p<p'\leq {\frac{1}{2}}$ , $0<z<{{a}/{2}}$ , and $n=z,z+2,\dots$ ,

(46) \begin{equation} \frac{\mathbb{P}_{p',z,a}(N=n)}{{\mathbb{P}}_{p,z,a}(N=n)} = \bigg(\frac{p'q'}{pq}\bigg)^{{n}/{2}}H_{p,p',z,a}\bigg(\frac{T_{z,a}^+(n)}{T_{z,a}(n)}\bigg), \end{equation}

where

\begin{equation*} H_{p,p',z,a}(x) = \frac{[({p'}/{q'})^{({a-z})/{2}} - ({q'}/{p'})^{{z}/{2}}]x + ({q'}/{p'})^{{z}/{2}}} {[({p}/{q})^{({a-z})/{2}} - ({q}/{p})^{{z}/{2}}]x + ({q}/{p})^{{z}/{2}}} \qquad \text{for } 0\le x \leq 1. \end{equation*}

Note that

(47) \begin{align} &\frac{{\mathrm{d}}}{{\mathrm{d}} x}H_{p,p',z,a}(x) \nonumber \\[5pt] & \quad = \bigg\{\bigg[\bigg(\frac{p}{q}\bigg)^{({a-z})/{2}} - \bigg(\frac{q}{p}\bigg)^{{z}/{2}}\bigg]x + \bigg(\frac{q}{p}\bigg)^{{z}/{2}}\bigg\}^{-2} \bigg(\frac{qq'}{pp'}\bigg)^{{z}/{2}}\bigg[\bigg({p'}/{q'}\bigg)^{{{a}/{2}}} - \bigg(\frac{p}{q}\bigg)^{{{a}/{2}}}\bigg] > 0. \end{align}

Since, by Theorem 2, ${T_{z,a}^+(n)}/{T_{z,a}(n)}$ is increasing in $n \in \{z,z+2,\dots\}$ , it follows from (46) and (47) that ${\mathbb{P}_{p',z,a}(N=n)}/{{\mathbb{P}}_{p,z,a}(N=n)}$ is increasing in $n \in \{z,z+2,\dots\}$ . This proves that $\{{\mathcal{L}}_{p,z,a}(N)\colon 0\le p \le {\frac{1}{2}}\}$ has monotone (increasing) likelihood ratio. For ${{a}/{2}}<z<a$ , note that $\mathcal{L}_{p,z,a}(N)=\mathcal{L}_{p',z',a}(N)$ with $p'=1-p$ and $z'=a-z$ , implying that $\{{\mathcal{L}}_{p,z,a}(N)\colon {\frac{1}{2}} \le p \le 1 \}$ has monotone (decreasing) likelihood ratio, completing the proof.

4. Proof of Theorem 4

Proof of Theorem 4. Fix $0<z<{{a}/{2}}$ . We claim that, for $n \geq 0$ ,

(48) \begin{equation} f(p,n)\;:\!=\;\mathbb{P}_{p,z, a}(N>n) \text{ is increasing in } p \in \big[0,{\tfrac{1}{2}}\big]. \end{equation}

Let

(49) \begin{equation} S_z(n)\;:\!=\;\{(\omega_1,\dots,\omega_n) \in \{-1,1\}^n\colon 0<z+\omega_1+\cdots+\omega_i<a, i=1,\dots,n\}, \end{equation}

and let $(\omega_1,\dots,\omega_n)_z\;:\!=\;\big(z,z+\omega_1,z+\omega_1+\omega_2, \dots, z+\sum_{i=1}^n \omega_i\big)$ , which is the sample path starting at z with successive increments $\omega_1,\dots, \omega_n$ . Since z is fixed, for convenience we may identify $(\omega_1,\dots,\omega_n)$ with the corresponding sample path $(\omega_1,\dots,\omega_n)_z$ . In particular, we refer to $S_z(n)$ as the collection of all sample paths starting at z and strictly staying between 0 and a up to time n. (By abusing notation, for $(\omega_1,\dots,\omega_{n}) \in S_{z}(n)$ , we also write $(\omega_1,\dots,\omega_{n})_z \in S_{z}(n)$ .)

We now prove (48) by induction on n. Plainly, (48) holds for $n=0$ . Suppose (48) holds for $n\leq m$ with some $m\geq 0$ . We need to show that

(50) \begin{equation} f(p,m+1) \text{ is increasing in } p\in\big[0,{\tfrac{1}{2}}\big]. \end{equation}

By (49), $f(p,m+1)\;:\!=\;\mathbb{P}_{p,z, a}(N>m+1)=\mathbb{P}\{(X_{1,p},\dots, X_{m+1,p}) \in S_{z}(m+1)\}$ , where the $X_{i,p}$ are defined as in (3). We partition the sample paths of $S_{z}(m+1)$ into subsets $\Delta_i$ , $i=0,1,\dots, m+1$ , where $\Delta_0$ is the subset of those sample paths that always stay below $a-1$ , and $\Delta_i$ ( $i=1,\dots, m+1$ ) is the subset of those sample paths that visit $a-1$ at time i for the first time. (Note that for $i \geq 1$ , $\Delta_i=\emptyset$ if i and $a-z-1$ have opposite parity.) Then $f(p,m+1)=\sum_{i=0}^{m+1} g(p,m+1,i)$ , where $g(p,m+1,i)\;:\!=\;\mathbb{P}\{(X_{1,p},\dots, X_{m+1,p})_{z} \in \Delta_i\}$ . To prove (50), it suffices to show that, for $i=0,1,\dots,m+1$ , $g(p,m+1,i)$ is increasing in $p \in \big[0,{\frac{1}{2}}\big]$ . To show $g(p,m+1,0)$ is increasing in $p \in \big[0,{\frac{1}{2}}\big]$ , we have

\begin{align*} g(p,m+1,0) & = \mathbb{P}\{(X_{1,p},\dots, X_{m+1,p})_{z} \in \Delta_0\} \\[5pt] & = \mathbb{P}\{(X_{1,p},\dots, X_{m+1,p})_{z} \text{ stays strictly between } 0 \text{ and } a-1\} \\[5pt] & = \mathbb{P}_{p,z, a-1}(N>m+1), \end{align*}

which, by Theorems 1 and 3, is increasing in $p \in \big[0,{\frac{1}{2}}\big]$ .

To show that $g(p,m+1,i)$ is increasing in $p \in \big[0,{\frac{1}{2}}\big]$ for $i=1,\dots, m+1$ , we further partition the $\Delta_i$ into $\Delta_{i,j}$ ( $i\leq j\le m+1$ ) where $\Delta_{i,i}$ is the subset of those sample paths that after time i never revisit z, and $\Delta_{i,j}$ ( $j>i$ ) is the subset of those sample paths that after time i revisit z at time j for the first time. Let $h(p,m+1,i,j)\;:\!=\;\mathbb{P}\{(X_{1,p},\dots, X_{m+1,p})_{z} \in \Delta_{i,j}\}$ . We have $g(p,m+1,i)=\sum_{j=i}^{m+1} h(p,m+1,i,j)$ . It suffices to show that each $h(p,m+1,i,j)$ is increasing in $p \in \big[0,{\frac{1}{2}}\big]$ .

For $i<j\leq m+1$ , let

\begin{align*} A_{i,j}\;:\!=\;\{(\omega_1,\dots,\omega_j) \in \{-1,1\}^j \colon & 0<z+\omega_1+\dots+\omega_\ell<a-1,\ell=1,\dots,i-1; \\[5pt] & z+\omega_1+\cdots+\omega_i=a-1; \\[5pt] & z<a-1+\omega_{i+1}+\cdots+\omega_\ell<a, \ell=i+1,\dots, j-1; \\[5pt] & \omega_{i+1}+\cdots+\omega_j=-(a-z-1)\}, \end{align*}

and

\begin{align*} S_{z}(m+1-j) & \;:\!=\; \{(\omega_1,\dots, \omega_{m+1-j}) \in \{-1,1\}^{m+1-j} \colon \\[5pt] & \qquad 0<z+\omega_1+\cdots+\omega_\ell<a,\ \ell=1,\dots, m+1-j\} \\[5pt] & = \{(\omega_{j+1},\dots, \omega_{m+1}) \in \{-1,1\}^{m+1-j} \colon \\[5pt] & \qquad 0<z+\omega_{j+1}+\cdots+\omega_\ell<a,\ \ell=j+1,\dots, m+1\}. \end{align*}

Since $(\omega_1,\dots, \omega_{m+1})_{z} \in \Delta_{i,j}$ if and only if $(\omega_1,\dots, \omega_{m+1}) \in A_{i,j} \times S_{z}(m+1-j)$ ,

(51) \begin{align} h(p,m+1,i,j) & = \mathbb{P}\{(X_{1,p},\dots, X_{m+1,p})_{z} \in \Delta_{i,j}\} \notag \\[5pt] & = \mathbb{P}\{(X_{1,p},\dots, X_{m+1,p}) \in A_{i,j} \times S_{z}(m+1-j)\} \notag \\[5pt] & = \mathbb{P}\{(X_{1,p},\dots, X_{j,p}) \in A_{i,j}\} \mathbb{P}\{(X_{j+1,p},\dots, X_{m+1,p}) \in S_{z}(m+1-j)\} \notag \\[5pt] & = \mathbb{P}\{(X_{1,p},\dots, X_{j,p}) \in A_{i,j}\} \mathbb{P}_{p,z,a}(N>m+1-j). \end{align}

By the induction hypothesis, $\mathbb{P}_{p,z,a}(N>m+1-j)$ is increasing in $p \in \big[0,{\frac{1}{2}}\big]$ . Also,

\begin{equation*} \mathbb{P}\{(X_{1,p},\dots, X_{j,p}) \in A_{i,j}\} = \begin{cases} (pq)^{j/2} |A_{i,j}| & \text{if } j \text{ is even}, \\[5pt] 0& \text{otherwise}, \end{cases} \end{equation*}

which is increasing in $p \in \big[0,{\frac{1}{2}}\big]$ . By (51), $h(p,m+1,i,j)$ is increasing in $p \in \big[0,{\frac{1}{2}}\big]$ .

It remains to show that $h(p,m+1,i,i)$ is increasing in $p \in \big[0,{\frac{1}{2}}\big]$ . Observe that each sample path $(\omega_1,\dots, \omega_{m+1})_{z} \in \Delta_{i,i}$ ends above z at time $m+1$ , so that there are more $+1$ increments than $-1$ increments. It follows that the probability of each sample path in $\Delta_{i,i}$ is increasing in $p \in \big[0,{\frac{1}{2}}\big]$ . Consequently, $h(p,m+1,i,i)=\mathbb{P}\{(X_{1,p},\dots, X_{m+1,p})_{z} \in \Delta_{i,i}\}$ is increasing in $p \in \big[0,{\frac{1}{2}}\big]$ . This completes the induction proof of (48).

It follows from (48) that, for $0<z<{{a}/{2}}$ , the distribution ${\mathcal{L}}_{p,z,a}(N)$ is stochastically increasing in $p \in \big[0,{\frac{1}{2}}\big]$ . Since $\mathcal{L}_{p,z,a}(N)=\mathcal{L}_{p',z',a}(N)$ for $p'=1-p$ and $z'=a-z$ , it follows that $\mathcal{L}_{p,z,a}(N)$ is stochastically decreasing in $p \in \big[{\frac{1}{2}},1\big]$ for ${{a}/{2}}<z<a$ . The proof is complete.