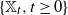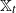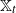1. Introduction
We consider a supercritical branching Lévy process. At time 0, we start with a single particle which moves according to a Lévy process
![]() $\{(\xi_t)_{t\ge 0},{\rm P}\}$
with Lévy exponent
$\{(\xi_t)_{t\ge 0},{\rm P}\}$
with Lévy exponent
![]() $\psi(\theta)=\log {\rm E}\big({\textrm{e}}^{{\textrm{i}} \theta \xi_1}\big)$
. The lifetime of each particle is exponentially distributed with parameter
$\psi(\theta)=\log {\rm E}\big({\textrm{e}}^{{\textrm{i}} \theta \xi_1}\big)$
. The lifetime of each particle is exponentially distributed with parameter
![]() $\beta$
, then it splits into k new particles with probability
$\beta$
, then it splits into k new particles with probability
![]() $p_k$
,
$p_k$
,
![]() $k\ge0$
. Once born, each particle will evolve independently, from its parent’s place of death, according to the same law as its parent, i.e. move according to the same Lévy process, and branch with the same branching rate and offspring distribution. We use
$k\ge0$
. Once born, each particle will evolve independently, from its parent’s place of death, according to the same law as its parent, i.e. move according to the same Lévy process, and branch with the same branching rate and offspring distribution. We use
![]() $\mathbb{P}$
to denote the law of the branching Lévy process. Expectations with respect to
$\mathbb{P}$
to denote the law of the branching Lévy process. Expectations with respect to
![]() $\mathbb{P}$
and P will be denoted by
$\mathbb{P}$
and P will be denoted by
![]() $\mathbb{E}$
and E respectively.
$\mathbb{E}$
and E respectively.
In this paper, we use ‘:=’ to denote a definition. For
![]() $a, b\in\mathbb{R}$
,
$a, b\in\mathbb{R}$
,
![]() $a \wedge b \,:\!=\, \min\{a, b\}$
. We will label each particle using the classical Ulam–Harris system. We write
$a \wedge b \,:\!=\, \min\{a, b\}$
. We will label each particle using the classical Ulam–Harris system. We write
![]() $\mathbb{T}$
for the set of all the particles in the tree, and o for the root of the tree. We also use the following notation:
$\mathbb{T}$
for the set of all the particles in the tree, and o for the root of the tree. We also use the following notation:
-
For any
 $u\in \mathbb{T}$
,
$u\in \mathbb{T}$
,
 $I_u^0$
denotes set of all the ancestors of u,
$I_u^0$
denotes set of all the ancestors of u,
 $I_u\,:\!=\,I_u^0\cup\{u\}$
, and
$I_u\,:\!=\,I_u^0\cup\{u\}$
, and
 $n^u$
is the number of particles in
$n^u$
is the number of particles in
 $I_u\setminus \{o\}$
.
$I_u\setminus \{o\}$
. -
For any
 $u\in \mathbb{T}$
,
$u\in \mathbb{T}$
,
 $\tau_u$
is the life length of u. Then
$\tau_u$
is the life length of u. Then
 $\{\tau_u,u\in\mathbb{T}\}$
are independent and identically distributed (i.i.d.), and exponentially distributed with parameter
$\{\tau_u,u\in\mathbb{T}\}$
are independent and identically distributed (i.i.d.), and exponentially distributed with parameter
 $\beta$
. Let
$\beta$
. Let
 $b_u$
and
$b_u$
and
 $\sigma_u$
be the birth and death times of u respectively. It is clear that
$\sigma_u$
be the birth and death times of u respectively. It is clear that
 $b_u=\sum_{v\in I_u^0}\tau_v$
and
$b_u=\sum_{v\in I_u^0}\tau_v$
and
 $\sigma_u=b_u+\tau_u$
. For any
$\sigma_u=b_u+\tau_u$
. For any
 $t\ge 0$
, let
$t\ge 0$
, let
 $\mathcal{F}_t^{\mathbb{T}}\, :\!=\, \sigma\{b_u\wedge t,\sigma_u\wedge t\colon u\in\mathbb{T}\}$
.
$\mathcal{F}_t^{\mathbb{T}}\, :\!=\, \sigma\{b_u\wedge t,\sigma_u\wedge t\colon u\in\mathbb{T}\}$
. -
For any
 $t\ge 0$
, let
$t\ge 0$
, let
 $\mathcal{L}_t$
be the set of all particles alive at time t.
$\mathcal{L}_t$
be the set of all particles alive at time t. -
Let
 $\{(X^u_s)_{s\ge 0}, u\in\mathbb{T}\}$
be i.i.d. with the same law as
$\{(X^u_s)_{s\ge 0}, u\in\mathbb{T}\}$
be i.i.d. with the same law as
 $\{(\xi_s)_{s\ge 0},{\rm P}\}$
and also independent of
$\{(\xi_s)_{s\ge 0},{\rm P}\}$
and also independent of
 $\{\tau_u,u\in\mathbb{T}\}$
.
$\{\tau_u,u\in\mathbb{T}\}$
. -
For
 $u\in\mathcal{L}_t$
, let
$u\in\mathcal{L}_t$
, let
 $\xi^u_t$
be the position of u at time t. Then, for
$\xi^u_t$
be the position of u at time t. Then, for
 $t\in [0, \sigma_o]$
,
$t\in [0, \sigma_o]$
,
 $\xi^o_t=X^o_t$
and, for any other
$\xi^o_t=X^o_t$
and, for any other
 $u\in \mathbb{T}$
, (1.1)where
$u\in \mathbb{T}$
, (1.1)where \begin{equation} \xi^u_t=\xi^{\pi(u)}_{\sigma_{\pi(u)}}+X^u_{t-b_u}=\sum_{v\in I_u^0}X^v_{\tau_v}+X^u_{t-b_u}, \qquad t\in [b_u, \sigma_u], \end{equation}
\begin{equation} \xi^u_t=\xi^{\pi(u)}_{\sigma_{\pi(u)}}+X^u_{t-b_u}=\sum_{v\in I_u^0}X^v_{\tau_v}+X^u_{t-b_u}, \qquad t\in [b_u, \sigma_u], \end{equation}
 $\pi(u)$
denotes the parent of u.
$\pi(u)$
denotes the parent of u.
-
For
 $t\ge 0$
,
$t\ge 0$
,
 $v\in \mathcal{L}_t$
, and
$v\in \mathcal{L}_t$
, and
 $u\in I_v$
, we set
$u\in I_v$
, we set
 $X_{u, t}\,:\!=\,\xi^u_{\sigma_u\wedge t}-\xi^u_{b_u\wedge t}$
. Note that
$X_{u, t}\,:\!=\,\xi^u_{\sigma_u\wedge t}-\xi^u_{b_u\wedge t}$
. Note that
 $X_{v, t}=X^v_{t-b_v}$
and
$X_{v, t}=X^v_{t-b_v}$
and
 $X_{u,t}=X^u_{\tau_u}$
for all
$X_{u,t}=X^u_{\tau_u}$
for all
 $u\in I^0_v$
.
$u\in I^0_v$
.
For
![]() $t\geq 0$
, define
$t\geq 0$
, define
![]() $\mathbb{X}_t\,:\!=\,\sum_{u\in\mathcal{L}_t}\delta_{\xi^u_t}$
. The measure-valued process
$\mathbb{X}_t\,:\!=\,\sum_{u\in\mathcal{L}_t}\delta_{\xi^u_t}$
. The measure-valued process
![]() $(\mathbb{X}_t)_{t\geq 0}$
is called a branching Lévy process. When
$(\mathbb{X}_t)_{t\geq 0}$
is called a branching Lévy process. When
![]() $\{(\xi_t)_{t\ge 0}, {\rm P}\}$
is a Brownian motion,
$\{(\xi_t)_{t\ge 0}, {\rm P}\}$
is a Brownian motion,
![]() $(\mathbb{X}_t)_{t\geq 0}$
is called a branching Brownian motion.
$(\mathbb{X}_t)_{t\geq 0}$
is called a branching Brownian motion.
Denote by
![]() $Z_t$
the number of particles alive at time t. It is well known that
$Z_t$
the number of particles alive at time t. It is well known that
![]() $(Z_t)_{\geq 0}$
is a continuous-time branching process. In this paper we consider the supercritical case, i.e.
$(Z_t)_{\geq 0}$
is a continuous-time branching process. In this paper we consider the supercritical case, i.e.
![]() $m\,:\!=\,\sum_k kp_k>1$
. Then
$m\,:\!=\,\sum_k kp_k>1$
. Then
![]() $\mathbb{P} (\mathcal{S})>0$
, where
$\mathbb{P} (\mathcal{S})>0$
, where
![]() $\mathcal{S}$
is the event of survival. The extinction probability
$\mathcal{S}$
is the event of survival. The extinction probability
![]() $\mathbb{P} (\mathcal{S}^\textrm{c})$
is the smallest root in (0,1) of the equation
$\mathbb{P} (\mathcal{S}^\textrm{c})$
is the smallest root in (0,1) of the equation
![]() $\sum_{k}p_k s^k =s$
; see, for instance, [Reference Athreya and Ney6, Section III.4]. Define
$\sum_{k}p_k s^k =s$
; see, for instance, [Reference Athreya and Ney6, Section III.4]. Define
The process
![]() $\big({\textrm{e}}^{-\lambda t}Z_t\big)_{t\ge 0}$
is a non-negative martingale and hence
$\big({\textrm{e}}^{-\lambda t}Z_t\big)_{t\ge 0}$
is a non-negative martingale and hence
For any two functions f and g on
![]() $[0,\infty)$
,
$[0,\infty)$
,
![]() $f\sim g$
as
$f\sim g$
as
![]() $s\to 0_+$
means that
$s\to 0_+$
means that
![]() $\lim_{s\downarrow 0}({f(s)}/{g(s)})=1$
. Similarly,
$\lim_{s\downarrow 0}({f(s)}/{g(s)})=1$
. Similarly,
![]() $f\sim g$
as
$f\sim g$
as
![]() $s\to \infty$
means that
$s\to \infty$
means that
![]() $\lim_{s\to\infty}({f(s)}/{g(s)})=1$
. Throughout this paper we assume the following two conditions hold.
$\lim_{s\to\infty}({f(s)}/{g(s)})=1$
. Throughout this paper we assume the following two conditions hold.
The first condition is that the offspring distribution satisfies the Kesten–Stigum condition:
-
(H1)
 $\sum_{k\ge 1} (k\log k) p_k<\infty$
.
$\sum_{k\ge 1} (k\log k) p_k<\infty$
.
Condition (H1) ensures that W is non-degenerate with
![]() $\mathbb{P} (W>0)=\mathbb{P} (\mathcal{S})$
. For more details, see [Reference Athreya and Ney6, Section III.7].
$\mathbb{P} (W>0)=\mathbb{P} (\mathcal{S})$
. For more details, see [Reference Athreya and Ney6, Section III.7].
The second condition is on the spatial motion:
-
(H2) There exist a complex constant
 $c_*$
with
$c_*$
with
 ${\textrm{Re}}(c_*)>0$
,
${\textrm{Re}}(c_*)>0$
,
 $\alpha\in(0,2)$
, and a function
$\alpha\in(0,2)$
, and a function
 $L(x)\,:\,\mathbb{R}_+\to \mathbb{R}_+$
slowly varying at
$L(x)\,:\,\mathbb{R}_+\to \mathbb{R}_+$
slowly varying at
 $\infty$
such that
$\infty$
such that
 $\psi(\theta)\sim -c_* \theta^{\alpha}L\big(\theta^{-1}\big)$
as
$\psi(\theta)\sim -c_* \theta^{\alpha}L\big(\theta^{-1}\big)$
as
 $\theta\to 0_+$
.
$\theta\to 0_+$
.
Since
![]() ${\textrm{e}}^{\psi(\theta)}={\rm E}\big({\textrm{e}}^{{\textrm{i}} \theta \xi_1}\big)$
, we have
${\textrm{e}}^{\psi(\theta)}={\rm E}\big({\textrm{e}}^{{\textrm{i}} \theta \xi_1}\big)$
, we have
![]() ${\textrm{Re}}(\psi)\le 0$
and
${\textrm{Re}}(\psi)\le 0$
and
![]() $\psi({-}\theta)=\overline{\psi(\theta)}$
. Thus,
$\psi({-}\theta)=\overline{\psi(\theta)}$
. Thus,
![]() $\psi(\theta)\sim -\overline{c_*} |\theta|^{\alpha}L\big(|\theta|^{-1}\big)$
as
$\psi(\theta)\sim -\overline{c_*} |\theta|^{\alpha}L\big(|\theta|^{-1}\big)$
as
![]() $\theta\to 0_-$
. Under condition (H2), we can prove (see Remark 2.1) that
$\theta\to 0_-$
. Under condition (H2), we can prove (see Remark 2.1) that
![]() ${\rm P} (|\xi_s|\ge x)\sim c s x^{-\alpha}L(x)$
as
${\rm P} (|\xi_s|\ge x)\sim c s x^{-\alpha}L(x)$
as
![]() $x\to\infty$
, i.e.
$x\to\infty$
, i.e.
![]() $|\xi_s|$
has regularly varying tails.
$|\xi_s|$
has regularly varying tails.
An important example satisfying (H2) is the strictly stable process.
Example 1.1.
(Stable process.) Let
![]() $\xi$
be a strictly
$\xi$
be a strictly
![]() $\alpha$
-stable process,
$\alpha$
-stable process,
![]() $\alpha\in (0,2)$
, on
$\alpha\in (0,2)$
, on
![]() $\mathbb{R}$
with Lévy measure
$\mathbb{R}$
with Lévy measure
where
![]() $c_1,c_2\ge 0$
,
$c_1,c_2\ge 0$
,
![]() $c_1+c_2>0$
, and if
$c_1+c_2>0$
, and if
![]() $\alpha=1$
,
$\alpha=1$
,
![]() $c_1=c_2=c$
. For
$c_1=c_2=c$
. For
![]() $\alpha\in(1,2)$
, by [Reference Sato36, Lemma 14.11, (14.19)] and the fact that
$\alpha\in(1,2)$
, by [Reference Sato36, Lemma 14.11, (14.19)] and the fact that
![]() $\Gamma({-}\alpha)=-\alpha\Gamma(1-\alpha)$
, we obtain that, for
$\Gamma({-}\alpha)=-\alpha\Gamma(1-\alpha)$
, we obtain that, for
![]() $\theta>0$
,
$\theta>0$
,
and, taking the conjugate on both sides of [Reference Sato36, Lemma 14.11 (14.19)], we get that
Thus, the Lévy exponent of
![]() $\xi$
is given, for
$\xi$
is given, for
![]() $\theta>0$
, by
$\theta>0$
, by
Similarly, by [Reference Sato36, Lemma 14.11 (14.18), (114.20)], we have, for
![]() $\theta>0$
,
$\theta>0$
,
 \begin{align} \psi(\theta) & = \left\{ \begin{array}{l@{\quad}l} \displaystyle\int\big({\textrm{e}}^{{\textrm{i}} \theta y}-1\big)\,n({\rm d}y), & \alpha\in (0,1), \\ \displaystyle\int({\textrm{e}}^{{\textrm{i}} \theta y}-1-{\textrm{i}} \theta y{\textbf{1}}_{|y|\le 1})\,n({\rm d}y)+{\textrm{i}} a\theta, & \alpha=1 \end{array}\right. \nonumber \\ & = \left\{ \begin{array}{ll} -\alpha\Gamma(1-\alpha)\big(c_1{\textrm{e}}^{-{\textrm{i}} \pi\alpha/2}+c_2{\textrm{e}}^{{\textrm{i}} \pi\alpha/2}\big)\theta^\alpha, &\quad \alpha\in(0,1), \\ -c\pi\theta+{\textrm{i}} a\theta, & \quad \alpha=1, \end{array}\right. \end{align}
\begin{align} \psi(\theta) & = \left\{ \begin{array}{l@{\quad}l} \displaystyle\int\big({\textrm{e}}^{{\textrm{i}} \theta y}-1\big)\,n({\rm d}y), & \alpha\in (0,1), \\ \displaystyle\int({\textrm{e}}^{{\textrm{i}} \theta y}-1-{\textrm{i}} \theta y{\textbf{1}}_{|y|\le 1})\,n({\rm d}y)+{\textrm{i}} a\theta, & \alpha=1 \end{array}\right. \nonumber \\ & = \left\{ \begin{array}{ll} -\alpha\Gamma(1-\alpha)\big(c_1{\textrm{e}}^{-{\textrm{i}} \pi\alpha/2}+c_2{\textrm{e}}^{{\textrm{i}} \pi\alpha/2}\big)\theta^\alpha, &\quad \alpha\in(0,1), \\ -c\pi\theta+{\textrm{i}} a\theta, & \quad \alpha=1, \end{array}\right. \end{align}
where
![]() $a\in\mathbb{R}$
is a constant. It is clear that
$a\in\mathbb{R}$
is a constant. It is clear that
![]() $\psi$
satisfies (H2). For more details on stable processes, we refer the reader to [Reference Sato36, Section 14].
$\psi$
satisfies (H2). For more details on stable processes, we refer the reader to [Reference Sato36, Section 14].
In Section 4 we give more examples satisfying condition (H2). Note that the non-symmetric 1-stable process does not satisfy (H2). However, in Example 4.1 we show that our main result still holds for the non-symmetric 1-stable process.
The maximal position
![]() $M_t\,:\!=\,\sup_{u\in\mathcal{L}_t}\xi^u_t$
of branching Brownian motions has been studied intensively. Assume that
$M_t\,:\!=\,\sup_{u\in\mathcal{L}_t}\xi^u_t$
of branching Brownian motions has been studied intensively. Assume that
![]() $\beta=1$
,
$\beta=1$
,
![]() $p_0=0$
, and
$p_0=0$
, and
![]() $m=2$
. The seminal paper [Reference Kolmogorov29] proved that
$m=2$
. The seminal paper [Reference Kolmogorov29] proved that
![]() $M_t/t\to \sqrt{2}$
in probability as
$M_t/t\to \sqrt{2}$
in probability as
![]() $t\to\infty$
. [Reference Bramson15] (see also [Reference Bramson16]) proved that, under some moment conditions,
$t\to\infty$
. [Reference Bramson15] (see also [Reference Bramson16]) proved that, under some moment conditions,
![]() $\mathbb{P} (M_t-m(t)\le x)\to 1-w(x)$
as
$\mathbb{P} (M_t-m(t)\le x)\to 1-w(x)$
as
![]() $t\to\infty$
for all
$t\to\infty$
for all
![]() $x\in \mathbb{R}$
, where
$x\in \mathbb{R}$
, where
![]() $m(t)=\sqrt{2}t-{3}/{2\sqrt{2}}\log t$
and w(x) is a traveling wave solution. For more works on
$m(t)=\sqrt{2}t-{3}/{2\sqrt{2}}\log t$
and w(x) is a traveling wave solution. For more works on
![]() $M_t$
, see [Reference Chauvin and Rouault19, Reference Chauvin and Rouault20, Reference Lalley and Sellke30, Reference Roberts35]. For inhomogeneous branching Brownian motions, many papers have discussed the growth rate of the maximal position; see [Reference Bocharov12–Reference Bocharov and Harris14] for the case with catalytic branching at the origin, and [Reference Lalley and Sellke31, Reference Lalley and Sellke32, Reference Nishimori and Shiozawa34, Reference Shiozawa37] for the case with some general branching mechanisms.
$M_t$
, see [Reference Chauvin and Rouault19, Reference Chauvin and Rouault20, Reference Lalley and Sellke30, Reference Roberts35]. For inhomogeneous branching Brownian motions, many papers have discussed the growth rate of the maximal position; see [Reference Bocharov12–Reference Bocharov and Harris14] for the case with catalytic branching at the origin, and [Reference Lalley and Sellke31, Reference Lalley and Sellke32, Reference Nishimori and Shiozawa34, Reference Shiozawa37] for the case with some general branching mechanisms.
Recently, the full statistics of the extremal configuration of branching Brownian motion have been studied. [Reference Arguin, Bovier and Kistler3, Reference Arguin, Bovier and Kistler4] studied the limit property of the extremal process of branching Brownian motion, proving that the random measure defined by
![]() $\mathcal{E}_t\,:\!=\,\sum_{u\in\mathcal{L}_t}\delta_{\xi^u_t-m(t)}$
converges weakly, and that the limiting process is a (randomly shifted) Poisson cluster process. Almost at the same time, [Reference Aïdékon, Berestycki, Brunet and Shi2] proved similar results using a totally different method.
$\mathcal{E}_t\,:\!=\,\sum_{u\in\mathcal{L}_t}\delta_{\xi^u_t-m(t)}$
converges weakly, and that the limiting process is a (randomly shifted) Poisson cluster process. Almost at the same time, [Reference Aïdékon, Berestycki, Brunet and Shi2] proved similar results using a totally different method.
For branching random walks, several authors have studied similar problems under an exponential moment assumption on the displacements of the offspring from the parent [Reference Aïdékon1, Reference Carmona and Hu18, Reference Hu and Shi27, Reference Madaule33]. When the displacements of the offspring from the parents are i.i.d. and have regularly varying tails, [Reference Durrett23] studied the limit property of its maximum displacement
![]() $M_n$
. More precisely, [Reference Durrett23] proved that
$M_n$
. More precisely, [Reference Durrett23] proved that
![]() $a_n^{-1}M_n$
converges weakly, where
$a_n^{-1}M_n$
converges weakly, where
![]() $a_n=m^{n/\alpha}L_0(m^n)$
and
$a_n=m^{n/\alpha}L_0(m^n)$
and
![]() $L_0$
is slowly varying at
$L_0$
is slowly varying at
![]() $\infty$
. Recently, the extremal processes of the branching random walks with regularly varying steps were studied in [Reference Bhattacharya, Hazra and Roy8, Reference Bhattacharya, Hazra and Roy9], where it was proved that the point random measure
$\infty$
. Recently, the extremal processes of the branching random walks with regularly varying steps were studied in [Reference Bhattacharya, Hazra and Roy8, Reference Bhattacharya, Hazra and Roy9], where it was proved that the point random measure
![]() $\sum_{|v|=n}\delta_{a_n^{-1}S_v}$
, where
$\sum_{|v|=n}\delta_{a_n^{-1}S_v}$
, where
![]() $S_v$
is the position of v, converges weakly to a Cox cluster process, which is quite different from the case with exponential moments. See also [Reference Bhattacharya, Maulik, Palmowski and Roy10, Reference Gantert25] for related works on branching random walks with heavy-tailed displacements.
$S_v$
is the position of v, converges weakly to a Cox cluster process, which is quite different from the case with exponential moments. See also [Reference Bhattacharya, Maulik, Palmowski and Roy10, Reference Gantert25] for related works on branching random walks with heavy-tailed displacements.
[Reference Shiozawa, Chen, Takeda and Uemura38] studied branching symmetric stable processes with branching rate
![]() $\mu$
being a measure on
$\mu$
being a measure on
![]() $\mathbb{R}$
in a Kato class with compact support (i.e. the support of
$\mathbb{R}$
in a Kato class with compact support (i.e. the support of
![]() $\mu$
is compact) and the offspring distribution
$\mu$
is compact) and the offspring distribution
![]() $\{p_n(x), n\geq 0\}$
being spatially dependent. Under some conditions on
$\{p_n(x), n\geq 0\}$
being spatially dependent. Under some conditions on
![]() $\mu$
and
$\mu$
and
![]() $\{p_n(x), n\geq 0\}$
, [Reference Shiozawa, Chen, Takeda and Uemura38] proved that the growth rate of the maximal displacement is exponential with rate given by the principal eigenvalue of the mean semigroup of the branching symmetric stable process. In this paper, we study the extremes of branching Lévy processes with constant branching rate
$\{p_n(x), n\geq 0\}$
, [Reference Shiozawa, Chen, Takeda and Uemura38] proved that the growth rate of the maximal displacement is exponential with rate given by the principal eigenvalue of the mean semigroup of the branching symmetric stable process. In this paper, we study the extremes of branching Lévy processes with constant branching rate
![]() $\beta$
(that is,
$\beta$
(that is,
![]() $\mu({\textrm{d}} x)=\beta\, {\textrm{d}} x$
) and spatial motion having regularly varying tails (see condition (H2)). Since
$\mu({\textrm{d}} x)=\beta\, {\textrm{d}} x$
) and spatial motion having regularly varying tails (see condition (H2)). Since
![]() $\beta\,{\textrm{d}} x$
is not compactly supported, we cannot get the growth rate of the maximal displacement from [Reference Shiozawa, Chen, Takeda and Uemura38]. As a corollary of our extreme limit result we get the growth rate of the maximal displacement, see Corollary 1.2.
$\beta\,{\textrm{d}} x$
is not compactly supported, we cannot get the growth rate of the maximal displacement from [Reference Shiozawa, Chen, Takeda and Uemura38]. As a corollary of our extreme limit result we get the growth rate of the maximal displacement, see Corollary 1.2.
The key idea of the proof in this paper is the ‘one large jump principle’ inspired by [Reference Bhattacharya, Hazra and Roy8, Reference Bhattacharya, Hazra and Roy9, Reference Durrett23]. Along the discrete times
![]() $n\delta$
, the branching Lévy process
$n\delta$
, the branching Lévy process
![]() $\{\mathbb{X}_{n\delta},n\ge 1\}$
is a branching random walk and the displacements from parents has the same law as
$\{\mathbb{X}_{n\delta},n\ge 1\}$
is a branching random walk and the displacements from parents has the same law as
![]() $\mathbb{X}_\delta$
. It is natural to think that we may get the results of this paper from the results for branching random walks by letting the time grid become finer and finer, and appropriately controlling the behavior between the time gaps. However, we cannot apply the results for branching random walks in [Reference Bhattacharya, Hazra and Roy8, Reference Bhattacharya, Hazra and Roy9, Reference Madaule33] to
$\mathbb{X}_\delta$
. It is natural to think that we may get the results of this paper from the results for branching random walks by letting the time grid become finer and finer, and appropriately controlling the behavior between the time gaps. However, we cannot apply the results for branching random walks in [Reference Bhattacharya, Hazra and Roy8, Reference Bhattacharya, Hazra and Roy9, Reference Madaule33] to
![]() $\{\mathbb{X}_{n\delta},n\ge 1\}$
. First, under condition (H2), the exponential moment assumption in [Reference Madaule33] is not satisfied. Second, [Reference Bhattacharya, Hazra and Roy8] assumes that the displacements are i.i.d., while the atoms of the random measure
$\{\mathbb{X}_{n\delta},n\ge 1\}$
. First, under condition (H2), the exponential moment assumption in [Reference Madaule33] is not satisfied. Second, [Reference Bhattacharya, Hazra and Roy8] assumes that the displacements are i.i.d., while the atoms of the random measure
![]() $\mathbb{X}_\delta$
, being particles alive at time
$\mathbb{X}_\delta$
, being particles alive at time
![]() $\delta$
in our branching Lévy process, are not independent. Last, although the displacements of offspring coming from the same parent are allowed to be dependent in [Reference Bhattacharya, Hazra and Roy9], [Reference Bhattacharya, Hazra and Roy9, Assumption 2.5], where the displacements from parents are given by a special form [Reference Bhattacharya, Hazra and Roy9, (2.9) and (2.10)]), seems to be very difficult to check for
$\delta$
in our branching Lévy process, are not independent. Last, although the displacements of offspring coming from the same parent are allowed to be dependent in [Reference Bhattacharya, Hazra and Roy9], [Reference Bhattacharya, Hazra and Roy9, Assumption 2.5], where the displacements from parents are given by a special form [Reference Bhattacharya, Hazra and Roy9, (2.9) and (2.10)]), seems to be very difficult to check for
![]() $\mathbb{X}_\delta$
.
$\mathbb{X}_\delta$
.
Branching Lévy processes are closely related to the Fisher–Kolmogorov–Petrovsky–Piskunov (Fisher–KPP) equation when the classical Laplacian
![]() $\Delta$
is replaced by the infinitesimal generator of the corresponding Lévy process. For any
$\Delta$
is replaced by the infinitesimal generator of the corresponding Lévy process. For any
![]() $g\in C_\textrm{b}^+(\mathbb{R})$
, define
$g\in C_\textrm{b}^+(\mathbb{R})$
, define
![]() $u_g(t,x)=\mathbb{E}\big(\exp\big\{{-}\sum_{v\in\mathcal{L}_t}g\big(\xi^v_t+x\big)\big\}\big)$
. By the Markov and branching properties, we have
$u_g(t,x)=\mathbb{E}\big(\exp\big\{{-}\sum_{v\in\mathcal{L}_t}g\big(\xi^v_t+x\big)\big\}\big)$
. By the Markov and branching properties, we have
 \begin{equation} u_g(t,x) = {\rm E}\big({\textrm{e}}^{-g(\xi_t+x)}\big) + {\rm E}\int_0^t \varphi\big(u_g\big(t-s,\xi_s+x\big)\big)\,\textrm{d}s,\end{equation}
\begin{equation} u_g(t,x) = {\rm E}\big({\textrm{e}}^{-g(\xi_t+x)}\big) + {\rm E}\int_0^t \varphi\big(u_g\big(t-s,\xi_s+x\big)\big)\,\textrm{d}s,\end{equation}
where
![]() $\varphi(s)=\beta\big(\sum_k s^kp_k-s\big)$
. Then
$\varphi(s)=\beta\big(\sum_k s^kp_k-s\big)$
. Then
![]() $1-u_g$
is a mild solution to
$1-u_g$
is a mild solution to
with initial data
![]() $u(0,x)=1-{\textrm{e}}^{-g(x)}$
, where
$u(0,x)=1-{\textrm{e}}^{-g(x)}$
, where
![]() $\mathcal{A}$
is the infinitesimal generator of
$\mathcal{A}$
is the infinitesimal generator of
![]() $\xi$
. [Reference Cabré and Roquejoffre17] proved that, under the assumption that the density of
$\xi$
. [Reference Cabré and Roquejoffre17] proved that, under the assumption that the density of
![]() $\xi$
is comparable to that of a symmetric
$\xi$
is comparable to that of a symmetric
![]() $\alpha$
-stable process, the frontal position of
$\alpha$
-stable process, the frontal position of
![]() $1-u$
is exponential in time. Using our main result, we give another proof of [Reference Cabré and Roquejoffre17, Theorem 1.5] and also partially generalize it; see Remark 5.1.
$1-u$
is exponential in time. Using our main result, we give another proof of [Reference Cabré and Roquejoffre17, Theorem 1.5] and also partially generalize it; see Remark 5.1.
1.1. Main results
Put
![]() ${\mathbb{R}}_0=({-}\infty,\infty)\setminus \{0\}$
, and
${\mathbb{R}}_0=({-}\infty,\infty)\setminus \{0\}$
, and
![]() $\overline{\mathbb{R}}_0=[{-}\infty,\infty]\setminus\{0\}$
with the topology generated by the set {
$\overline{\mathbb{R}}_0=[{-}\infty,\infty]\setminus\{0\}$
with the topology generated by the set {
![]() $(a,b)$
,
$(a,b)$
,
![]() $({-}b,-a), (a,\infty], [{-}\infty,-a) \,:\, 0<a<b\le \infty$
}. Note that, for any
$({-}b,-a), (a,\infty], [{-}\infty,-a) \,:\, 0<a<b\le \infty$
}. Note that, for any
![]() $a>0$
,
$a>0$
,
![]() $[a,\infty]$
and
$[a,\infty]$
and
![]() $[{-}\infty,-a]$
are compact subsets of
$[{-}\infty,-a]$
are compact subsets of
![]() $\overline{\mathbb{R}}_0$
. Denote by
$\overline{\mathbb{R}}_0$
. Denote by
![]() $\mathcal{B}_\textrm{b}^+\big(\overline{\mathbb{R}}_0\big)$
the set of all bounded non-negative Borel functions on
$\mathcal{B}_\textrm{b}^+\big(\overline{\mathbb{R}}_0\big)$
the set of all bounded non-negative Borel functions on
![]() $\overline{\mathbb{R}}_0$
. Let
$\overline{\mathbb{R}}_0$
. Let
![]() $C_\textrm{c}^+\big(\overline{\mathbb{R}}_0\big)$
be the set of all non-negative continuous functions on
$C_\textrm{c}^+\big(\overline{\mathbb{R}}_0\big)$
be the set of all non-negative continuous functions on
![]() $\overline{\mathbb{R}}_0$
such that
$\overline{\mathbb{R}}_0$
such that
![]() $g=0$
on
$g=0$
on
![]() $({-}\delta,0)\cup(0,\delta)$
for some
$({-}\delta,0)\cup(0,\delta)$
for some
![]() $\delta>0$
. Denote by
$\delta>0$
. Denote by
![]() $\mathcal{M}\big(\overline{\mathbb{R}}_0\big) $
the set of all Radon measures endowed with the topology of vague convergence (denoted by
$\mathcal{M}\big(\overline{\mathbb{R}}_0\big) $
the set of all Radon measures endowed with the topology of vague convergence (denoted by
![]() $\overset{\textrm{v}}{\to}$
), generated by the maps
$\overset{\textrm{v}}{\to}$
), generated by the maps
![]() $\mu\to \int f \,{\textrm{d}}\mu$
for all
$\mu\to \int f \,{\textrm{d}}\mu$
for all
![]() $f\in C_\textrm{c}^+\big(\overline{\mathbb{R}}_0\big)$
. Then
$f\in C_\textrm{c}^+\big(\overline{\mathbb{R}}_0\big)$
. Then
![]() $\mathcal{M}\big(\overline{\mathbb{R}}_0\big)$
is a metrizable space, see [Reference Kallenberg28, Theorem 4.2, p. 112]. For any
$\mathcal{M}\big(\overline{\mathbb{R}}_0\big)$
is a metrizable space, see [Reference Kallenberg28, Theorem 4.2, p. 112]. For any
![]() $g\in\mathcal{B}_\textrm{b}^+\big(\overline{\mathbb{R}}_0\big)$
and
$g\in\mathcal{B}_\textrm{b}^+\big(\overline{\mathbb{R}}_0\big)$
and
![]() $\mu\in\mathcal{M}\big(\overline{\mathbb{R}}_0\big)$
, we write
$\mu\in\mathcal{M}\big(\overline{\mathbb{R}}_0\big)$
, we write
![]() $\mu(g)\,:\!=\,\int_{\overline{\mathbb{R}}_0} g(x)\,\mu({\rm d} x)$
. A sequence of random elements
$\mu(g)\,:\!=\,\int_{\overline{\mathbb{R}}_0} g(x)\,\mu({\rm d} x)$
. A sequence of random elements
![]() $\nu_n$
in
$\nu_n$
in
![]() $\mathcal{M}\big(\overline{\mathbb{R}}_0\big)$
converges weakly to
$\mathcal{M}\big(\overline{\mathbb{R}}_0\big)$
converges weakly to
![]() $\nu$
, denoted as
$\nu$
, denoted as
![]() $\nu_n\overset{\textrm{d}}{\to}\nu$
, if and only if, for all
$\nu_n\overset{\textrm{d}}{\to}\nu$
, if and only if, for all
![]() $g\in C_\textrm{c}^+\big(\overline{\mathbb{R}}_0\big)$
,
$g\in C_\textrm{c}^+\big(\overline{\mathbb{R}}_0\big)$
,
![]() $\nu_n(g)$
converges weakly to
$\nu_n(g)$
converges weakly to
![]() $\nu(g)$
.
$\nu(g)$
.
We claim that there exists a non-decreasing function
![]() $h_t$
with
$h_t$
with
![]() $h_t\uparrow\infty$
such that
$h_t\uparrow\infty$
such that
where
![]() $\lambda$
is defined by (1.2). In fact, using [Reference Bingham, Goldie and Teugels11, Theorem 1.5.4], there exists a non-increasing function g such that
$\lambda$
is defined by (1.2). In fact, using [Reference Bingham, Goldie and Teugels11, Theorem 1.5.4], there exists a non-increasing function g such that
![]() $g(x)\sim x^{-\alpha}L(x)$
as
$g(x)\sim x^{-\alpha}L(x)$
as
![]() $x\to\infty$
. Then
$x\to\infty$
. Then
![]() $g(x)\to 0$
as
$g(x)\to 0$
as
![]() $x\to\infty$
. Define
$x\to\infty$
. Define
![]() $h_t\,:\!=\,\inf\{x>0\,:\, g(x)\le {\textrm{e}}^{-\lambda t}\}$
. It is clear that
$h_t\,:\!=\,\inf\{x>0\,:\, g(x)\le {\textrm{e}}^{-\lambda t}\}$
. It is clear that
![]() $h_t$
is non-decreasing and
$h_t$
is non-decreasing and
![]() $h_t\uparrow\infty$
. By the definition of
$h_t\uparrow\infty$
. By the definition of
![]() $h_t$
, for any
$h_t$
, for any
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
![]() $g(h_t/(1+\varepsilon)) \ge {\textrm{e}}^{-\lambda t} \ge g(h_t(1+\varepsilon))$
, which implies that
$g(h_t/(1+\varepsilon)) \ge {\textrm{e}}^{-\lambda t} \ge g(h_t(1+\varepsilon))$
, which implies that
 \begin{align*} (1+\varepsilon)^{-\alpha} & = (1+\varepsilon)^{-\alpha}\lim_{t\to\infty}\frac{L(h_t)}{L(h_t/(1+\varepsilon))} = \lim_{t\to\infty}\frac{g(h_t)}{g(h_t/(1+\varepsilon))} \\ & \le \liminf_{t\to\infty}{\textrm{e}}^{\lambda t}g(h_t) \le \limsup_{t\to\infty}{\textrm{e}}^{\lambda t}g(h_t) \\ & \le \lim_{t\to\infty}\frac{g(h_t)}{g(h_t(1+\varepsilon))} = (1+\varepsilon)^{\alpha} \lim_{t\to\infty}\frac{L(h_t)}{L(h_t(1+\varepsilon))} = (1+\varepsilon)^{\alpha}.\end{align*}
\begin{align*} (1+\varepsilon)^{-\alpha} & = (1+\varepsilon)^{-\alpha}\lim_{t\to\infty}\frac{L(h_t)}{L(h_t/(1+\varepsilon))} = \lim_{t\to\infty}\frac{g(h_t)}{g(h_t/(1+\varepsilon))} \\ & \le \liminf_{t\to\infty}{\textrm{e}}^{\lambda t}g(h_t) \le \limsup_{t\to\infty}{\textrm{e}}^{\lambda t}g(h_t) \\ & \le \lim_{t\to\infty}\frac{g(h_t)}{g(h_t(1+\varepsilon))} = (1+\varepsilon)^{\alpha} \lim_{t\to\infty}\frac{L(h_t)}{L(h_t(1+\varepsilon))} = (1+\varepsilon)^{\alpha}.\end{align*}
Since
![]() $\varepsilon$
is arbitrary, we get
$\varepsilon$
is arbitrary, we get
![]() $\lim_{t\to\infty}{\textrm{e}}^{\lambda t}h_t^{-\alpha}L(h_t)=\lim_{t\to\infty}{\textrm{e}}^{\lambda t} g(h_t)=1$
. In particular,
$\lim_{t\to\infty}{\textrm{e}}^{\lambda t}h_t^{-\alpha}L(h_t)=\lim_{t\to\infty}{\textrm{e}}^{\lambda t} g(h_t)=1$
. In particular,
![]() $h_t={\textrm{e}}^{\lambda t/\alpha}$
if
$h_t={\textrm{e}}^{\lambda t/\alpha}$
if
![]() $L=1$
. In Lemma 2.1 we prove that
$L=1$
. In Lemma 2.1 we prove that
![]() ${\textrm{e}}^{\lambda t}{\rm P}(h_t^{-1}\xi_s\in\cdot)\overset{\textrm{v}}{\to } sv_\alpha({\cdot})$
, where
${\textrm{e}}^{\lambda t}{\rm P}(h_t^{-1}\xi_s\in\cdot)\overset{\textrm{v}}{\to } sv_\alpha({\cdot})$
, where
with
![]() $q_1$
and
$q_1$
and
![]() $q_2$
being non-negative numbers, uniquely determined by
$q_2$
being non-negative numbers, uniquely determined by
![]() $c_*=\alpha\Gamma(1-\alpha)(q_1{\textrm{e}}^{-{\textrm{i}} \pi\alpha/2} + q_2{\textrm{e}}^{{\textrm{i}} \pi\alpha/2})$
if
$c_*=\alpha\Gamma(1-\alpha)(q_1{\textrm{e}}^{-{\textrm{i}} \pi\alpha/2} + q_2{\textrm{e}}^{{\textrm{i}} \pi\alpha/2})$
if
![]() $\alpha\neq 1$
and
$\alpha\neq 1$
and
![]() $q_1=q_2={\textrm{Re}}(c_*)/\pi$
if
$q_1=q_2={\textrm{Re}}(c_*)/\pi$
if
![]() $\alpha=1$
.
$\alpha=1$
.
Now we are ready to state our main result. Define a renormalized version of
![]() $\mathbb{X}_t$
by
$\mathbb{X}_t$
by
In this paper we will investigate the limit of
![]() $\mathcal{N}_t$
as
$\mathcal{N}_t$
as
![]() $t\to\infty$
.
$t\to\infty$
.
Theorem 1.1.
Under
![]() $\mathbb{P}$
,
$\mathbb{P}$
,
![]() $\mathcal{N}_t$
converges weakly to a random measure
$\mathcal{N}_t$
converges weakly to a random measure
![]() $\mathcal{N}_\infty \in \mathcal{M}\big(\overline{\mathbb{R}}_0\big)$
defined on some extension
$\mathcal{N}_\infty \in \mathcal{M}\big(\overline{\mathbb{R}}_0\big)$
defined on some extension
![]() $(\Omega,{\mathcal{G}},P)$
of the probability space on which the branching Lévy process is defined, with Laplace transform given by
$(\Omega,{\mathcal{G}},P)$
of the probability space on which the branching Lévy process is defined, with Laplace transform given by
where
![]() $\lambda$
is defined in (1.2) and W is the martingale limit defined in (1.3). Moreover,
$\lambda$
is defined in (1.2) and W is the martingale limit defined in (1.3). Moreover,
![]() $\mathcal{N}_\infty=\sum_{j}T_j\delta_{e_j}$
, where, given W,
$\mathcal{N}_\infty=\sum_{j}T_j\delta_{e_j}$
, where, given W,
![]() $\sum_{j}\delta_{e_j}$
is a Poisson random measure with intensity
$\sum_{j}\delta_{e_j}$
is a Poisson random measure with intensity
![]() $\vartheta Wv_\alpha({\textrm{d}} x)$
,
$\vartheta Wv_\alpha({\textrm{d}} x)$
,
![]() $\{T_j,j\ge 1\}$
is a sequence of i.i.d. random variables with common law
$\{T_j,j\ge 1\}$
is a sequence of i.i.d. random variables with common law
where
![]() $v_\alpha({\textrm{d}} x)$
is given by (1.8),
$v_\alpha({\textrm{d}} x)$
is given by (1.8),
![]() $Z_r$
is the number of particles alive at time r,
$Z_r$
is the number of particles alive at time r,
![]() $\vartheta=\int_0^\infty{\textrm{e}}^{-\lambda r}\mathbb{P}(Z_r>0)\,{\rm d}r$
, and
$\vartheta=\int_0^\infty{\textrm{e}}^{-\lambda r}\mathbb{P}(Z_r>0)\,{\rm d}r$
, and
![]() $\sum_{j}\delta_{e_j}$
and
$\sum_{j}\delta_{e_j}$
and
![]() $\{T_j,j\ge 1\}$
are independent.
$\{T_j,j\ge 1\}$
are independent.
Theorem 1.1 says that, given W,
![]() $\mathcal{N}_\infty$
is an integer-valued random measure with the locations of the atoms being a Poisson random measure with intensity
$\mathcal{N}_\infty$
is an integer-valued random measure with the locations of the atoms being a Poisson random measure with intensity
![]() $\vartheta Wv_\alpha({\textrm{d}} x)$
and with weights being i.i.d. with common distribution given by (1.10).
$\vartheta Wv_\alpha({\textrm{d}} x)$
and with weights being i.i.d. with common distribution given by (1.10).
The proof of Theorem 1.1 consists of two steps. First, we use the idea of ‘one large jump’, which has been used in [Reference Bhattacharya, Hazra and Roy8, Reference Bhattacharya, Hazra and Roy9, Reference Durrett23] for branching random walks, to deduce that
![]() $\mathcal{N}_t$
has the same limit as the family of random measures defined by
$\mathcal{N}_t$
has the same limit as the family of random measures defined by
By ‘one large jump’ we mean that with large probability, for all
![]() $v \in \mathcal{L}_t$
, at most one of the ancestors of v has a large enough movement. Then we prove that with large probability, for all u born before
$v \in \mathcal{L}_t$
, at most one of the ancestors of v has a large enough movement. Then we prove that with large probability, for all u born before
![]() $t-s$
,
$t-s$
,
![]() $\big|h_t^{-1}X_{u,t}\big|$
is small. Thus, the main contribution to
$\big|h_t^{-1}X_{u,t}\big|$
is small. Thus, the main contribution to
![]() $\widetilde{\mathcal{N}}_t$
is
$\widetilde{\mathcal{N}}_t$
is
Remark 1.1. Given a function f, we use
![]() $D_f$
to denote its set of discontinuity points. Then, by Theorem 1.1,
$D_f$
to denote its set of discontinuity points. Then, by Theorem 1.1,
![]() $\mathcal{N}_t(f)\overset{\textrm{d}}{\to}\mathcal{N}_\infty(f)$
for any bounded measurable function f on
$\mathcal{N}_t(f)\overset{\textrm{d}}{\to}\mathcal{N}_\infty(f)$
for any bounded measurable function f on
![]() $\overline{\mathbb{R}}_0$
with compact support satisfying
$\overline{\mathbb{R}}_0$
with compact support satisfying
![]() $\mathcal{N}_{\infty}(D_f)=0$
P-a.s. Furthermore, for any
$\mathcal{N}_{\infty}(D_f)=0$
P-a.s. Furthermore, for any
![]() $k\ge1$
,
$k\ge1$
,
where
![]() $\{B_j\}$
are relatively compact subsets of
$\{B_j\}$
are relatively compact subsets of
![]() $\overline{\mathbb{R}}_0$
satisfying
$\overline{\mathbb{R}}_0$
satisfying
![]() $\mathcal{N}_\infty(\partial B_j)=0$
,
$\mathcal{N}_\infty(\partial B_j)=0$
,
![]() $j=1,\ldots,k$
, P-a.s. See [Reference Kallenberg28, Theorem 4.4] for a proof.
$j=1,\ldots,k$
, P-a.s. See [Reference Kallenberg28, Theorem 4.4] for a proof.
Now we list the positions of all particles alive at time t in decreasing order,
![]() $M_{t,1}\ge M_{t,2}\ge \cdots \ge M_{t,Z_t},$
and for
$M_{t,1}\ge M_{t,2}\ge \cdots \ge M_{t,Z_t},$
and for
![]() $n>Z_t$
define
$n>Z_t$
define
![]() $M_{t,n}\,:\!=\,-\infty$
. In particular,
$M_{t,n}\,:\!=\,-\infty$
. In particular,
![]() $M_{t,1}=\max_{v\in\mathcal{L}_t}\xi^v_t$
is the rightmost position of the particles alive at time t. Note that
$M_{t,1}=\max_{v\in\mathcal{L}_t}\xi^v_t$
is the rightmost position of the particles alive at time t. Note that
![]() $v_\alpha(0,\infty)=\infty$
if and only if
$v_\alpha(0,\infty)=\infty$
if and only if
![]() $q_1>0$
. By the definition of
$q_1>0$
. By the definition of
![]() $\mathcal{N}_\infty$
in Theorem 1.1, we have that if
$\mathcal{N}_\infty$
in Theorem 1.1, we have that if
![]() $q_1=0$
then
$q_1=0$
then
![]() $P(\mathcal{N}_\infty(0,\infty)=0)=P\big(\sum_j {\textbf{1}}_{e_j>0}=0\big)=1$
. If
$P(\mathcal{N}_\infty(0,\infty)=0)=P\big(\sum_j {\textbf{1}}_{e_j>0}=0\big)=1$
. If
![]() $q_1>0$
then
$q_1>0$
then
and since, for any
![]() $x>0$
,
$x>0$
,
![]() $v_\alpha(x,\infty)<\infty$
, we have
$v_\alpha(x,\infty)<\infty$
, we have
Thus, on the set
![]() $\mathcal{S}$
, we can order the atoms of
$\mathcal{S}$
, we can order the atoms of
![]() $\mathcal{N}_\infty$
on
$\mathcal{N}_\infty$
on
![]() $(0,\infty)$
in decreasing order:
$(0,\infty)$
in decreasing order:
![]() $M_{(1)}\ge M_{(2)}\ge \cdots \ge M_{(k)}\ge \cdots\to 0$
. On the set
$M_{(1)}\ge M_{(2)}\ge \cdots \ge M_{(k)}\ge \cdots\to 0$
. On the set
![]() $\mathcal{S}^\textrm{c}$
,
$\mathcal{S}^\textrm{c}$
,
![]() $\mathcal{N}_{\infty}$
is null; then we define
$\mathcal{N}_{\infty}$
is null; then we define
![]() $M_{(k)}=-\infty$
for
$M_{(k)}=-\infty$
for
![]() $k\geq 1$
.
$k\geq 1$
.
Define
![]() $\mathbb{P}^*({\cdot}) \,:\!=\, \mathbb{P}(\cdot\mid\mathcal{S})$
$\mathbb{P}^*({\cdot}) \,:\!=\, \mathbb{P}(\cdot\mid\mathcal{S})$
![]() $(P^*({\cdot})\,:\!=\,P(\cdot\mid\mathcal{S}))$
and let
$(P^*({\cdot})\,:\!=\,P(\cdot\mid\mathcal{S}))$
and let
![]() $\mathbb{E}^*$
$\mathbb{E}^*$
![]() $(E^*)$
be the corresponding expectation. As a consequence of Theorem 1.1, we have the following corollary.
$(E^*)$
be the corresponding expectation. As a consequence of Theorem 1.1, we have the following corollary.
Corollary 1.1.
If
![]() $q_1>0$
then, for any
$q_1>0$
then, for any
![]() $n\ge1$
,
$n\ge1$
,
Moreover,
![]() $M_{(k)}>0$
,
$M_{(k)}>0$
,
![]() $k\geq 1$
,
$k\geq 1$
,
![]() $P^*$
-a.s.
$P^*$
-a.s.
In particular, for the rightmost position
![]() $R_t\,:\!=\,M_{t,1}=\max_{v\in\mathcal{L}_t}\xi^v_t$
, we have the following result.
$R_t\,:\!=\,M_{t,1}=\max_{v\in\mathcal{L}_t}\xi^v_t$
, we have the following result.
Corollary 1.2.
If
![]() $q_1>0$
then
$q_1>0$
then
![]() $\big(h^{-1}_t R_t;\, \mathbb{P}^*\big) \overset{\textrm{d}}{\to} \big(M_{(1)};\, P^*\big)$
, where the law of
$\big(h^{-1}_t R_t;\, \mathbb{P}^*\big) \overset{\textrm{d}}{\to} \big(M_{(1)};\, P^*\big)$
, where the law of
![]() $\big(M_{(1)};\, P^*\big)$
is given by
$\big(M_{(1)};\, P^*\big)$
is given by
Proof. Using Corollary 1.1,
![]() $\big(h^{-1}_tR_t;\, \mathbb{P}^*\big)\overset{\textrm{d}}{\to}\big(M_{(1)};\, P^*\big),$
and
$\big(h^{-1}_tR_t;\, \mathbb{P}^*\big)\overset{\textrm{d}}{\to}\big(M_{(1)};\, P^*\big),$
and
![]() $M_{(1)}>0$
$M_{(1)}>0$
![]() $P^*$
-a.s. For any
$P^*$
-a.s. For any
![]() $x>0$
,
$x>0$
,
![]() $P^*(M_{(1)}\le x) = P^*(\mathcal{N}_\infty(x,\infty)=0) = P^*\big(\sum_j {\textbf{1}}_{(x,\infty)}(e_j)=0\big) = \mathbb{E}^*\big({\textrm{e}}^{-\vartheta W v_\alpha(x,\infty)}\big) = \mathbb{E}^*\big({\textrm{e}}^{-\alpha^{-1}q_1\vartheta W x^{-\alpha}}\big)$
. The proof is now complete.
$P^*(M_{(1)}\le x) = P^*(\mathcal{N}_\infty(x,\infty)=0) = P^*\big(\sum_j {\textbf{1}}_{(x,\infty)}(e_j)=0\big) = \mathbb{E}^*\big({\textrm{e}}^{-\vartheta W v_\alpha(x,\infty)}\big) = \mathbb{E}^*\big({\textrm{e}}^{-\alpha^{-1}q_1\vartheta W x^{-\alpha}}\big)$
. The proof is now complete.
Remark 1.2. Similarly, we can order the particles alive at time t in an increasing order:
![]() $L_{t,1}\le L_{t,2}\le \cdots\le L_{t,Z_t}$
. When
$L_{t,1}\le L_{t,2}\le \cdots\le L_{t,Z_t}$
. When
![]() $q_2=0$
,
$q_2=0$
,
![]() $P(\mathcal{N}_\infty({-}\infty,0)=0)=P\big(\sum_j {\textbf{1}}_{e_j<0}=0\big)=1$
. When
$P(\mathcal{N}_\infty({-}\infty,0)=0)=P\big(\sum_j {\textbf{1}}_{e_j<0}=0\big)=1$
. When
![]() $q_2>0$
, on the set
$q_2>0$
, on the set
![]() $\mathcal{S}$
, we can order the atoms of
$\mathcal{S}$
, we can order the atoms of
![]() $\mathcal{N}_\infty$
on
$\mathcal{N}_\infty$
on
![]() $({-}\infty,0)$
as
$({-}\infty,0)$
as
![]() $L_{(1)}\le L_{(2)}\le \cdots \le L_{(k)}\le \cdots\to 0$
. Note that
$L_{(1)}\le L_{(2)}\le \cdots \le L_{(k)}\le \cdots\to 0$
. Note that
![]() $\{M_{(k)},k\ge1\}$
and
$\{M_{(k)},k\ge1\}$
and
![]() $\{L_{(k)},k\ge 1\}$
cover all the atoms of
$\{L_{(k)},k\ge 1\}$
cover all the atoms of
![]() $\mathcal{N}_\infty$
. Similar to Corollaries 1.1 and 1.2, we have the following weak convergence of
$\mathcal{N}_\infty$
. Similar to Corollaries 1.1 and 1.2, we have the following weak convergence of
![]() $(L_{t,1}, L_{t,2},\ldots,L_{t,n})$
: if
$(L_{t,1}, L_{t,2},\ldots,L_{t,n})$
: if
![]() $q_2>0$
then, for any
$q_2>0$
then, for any
![]() $n\ge1$
,
$n\ge1$
,
and the distribution of
![]() $L_{(1)}$
under
$L_{(1)}$
under
![]() $P^*$
is as follows: for any
$P^*$
is as follows: for any
![]() $x<0$
,
$x<0$
,
 $P^*(L_{(1)}\le x) = P^*(\mathcal{N}_\infty({-}\infty,x]>0) = P^*\big(\sum_j{\textbf{1}}_{({-}\infty,x]}(e_j)>0\big) = 1 - \mathbb{E}^*\big({\textrm{e}}^{-\vartheta W v_\alpha({-}\infty,x]}\big) = 1 - \mathbb{E}^*\Big({\textrm{e}}^{-\alpha^{-1}q_2\vartheta W |x|^{-\alpha}}\Big)$
.
$P^*(L_{(1)}\le x) = P^*(\mathcal{N}_\infty({-}\infty,x]>0) = P^*\big(\sum_j{\textbf{1}}_{({-}\infty,x]}(e_j)>0\big) = 1 - \mathbb{E}^*\big({\textrm{e}}^{-\vartheta W v_\alpha({-}\infty,x]}\big) = 1 - \mathbb{E}^*\Big({\textrm{e}}^{-\alpha^{-1}q_2\vartheta W |x|^{-\alpha}}\Big)$
.
The rest of the paper is organized as follows. In Section 2 we introduce the one large jump principle and give the proof of Theorem 1.1 based on Proposition 2.1, which will be proved in Section 2.3. The proof of Corollary 1.1 is given in Section 3. In Section 4 we give more examples satisfying condition (H2) and conditions which are weaker than (H2), but sufficient for the main result of this paper. We discuss the front position of the Fisher–KPP equation (1.6) in Section 5.
2. Proof of Theorem 1.1
2.1. Preliminaries
Recall that
![]() $h_t$
is a function satisfying (1.7). Let
$h_t$
is a function satisfying (1.7). Let
![]() $C_\textrm{b}^0(\mathbb{R})$
be the set of all bounded continuous functions vanishing in a neighborhood of 0. It is clear that if
$C_\textrm{b}^0(\mathbb{R})$
be the set of all bounded continuous functions vanishing in a neighborhood of 0. It is clear that if
![]() $g\in C_\textrm{c}^+\big(\overline{\mathbb{R}}_0\big)$
then
$g\in C_\textrm{c}^+\big(\overline{\mathbb{R}}_0\big)$
then
![]() $g^*(x)\,:\!=\,{\textbf{1}}_{\mathbb{R}_{0}}(x) g(x) \in C_\textrm{b}^0(\mathbb{R})$
.
$g^*(x)\,:\!=\,{\textbf{1}}_{\mathbb{R}_{0}}(x) g(x) \in C_\textrm{b}^0(\mathbb{R})$
.
Lemma 2.1.
For any
![]() $g\in C_\textrm{b}^0(\mathbb{R})$
and
$g\in C_\textrm{b}^0(\mathbb{R})$
and
![]() $s>0$
,
$s>0$
,
![]() $\lim_{t\to\infty}{\textrm{e}}^{\lambda t}{\rm E}\big(g\big(h_t^{-1}\xi_s\big)\big) = s\int_{\mathbb{R}_0}g(x)\,v_\alpha({\rm d}x)$
.
$\lim_{t\to\infty}{\textrm{e}}^{\lambda t}{\rm E}\big(g\big(h_t^{-1}\xi_s\big)\big) = s\int_{\mathbb{R}_0}g(x)\,v_\alpha({\rm d}x)$
.
Proof. Let
![]() $\nu_t$
be the law of
$\nu_t$
be the law of
![]() $h_t^{-1}\xi_s$
. Then, by (H2), as
$h_t^{-1}\xi_s$
. Then, by (H2), as
![]() $t\to\infty$
,
$t\to\infty$
,
where
Note that the left-hand side of (2.1) is the characteristic function of an infinitely divisible random variable
![]() $Y_t$
with Lévy measure
$Y_t$
with Lévy measure
![]() ${\textrm{e}}^{\lambda t}\nu_t$
, and, by (1.4),
${\textrm{e}}^{\lambda t}\nu_t$
, and, by (1.4),
![]() ${\textrm{e}}^{s\widetilde{\psi}(\theta)}$
is the characteristic function of a strictly
${\textrm{e}}^{s\widetilde{\psi}(\theta)}$
is the characteristic function of a strictly
![]() $\alpha$
-stable random variable Y with Lévy measure
$\alpha$
-stable random variable Y with Lévy measure
![]() $sv_\alpha(dx)$
. Thus,
$sv_\alpha(dx)$
. Thus,
![]() $Y_t$
weakly converges to Y. The desired result follows immediately from [Reference Sato36, Theorem 8.7 (1)].
$Y_t$
weakly converges to Y. The desired result follows immediately from [Reference Sato36, Theorem 8.7 (1)].
It is well known (see [Reference Bingham, Goldie and Teugels11, Theorem 1.5.6], for instance) that, for any
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $a_\varepsilon>0$
such that, for any
$a_\varepsilon>0$
such that, for any
![]() $y>a_{\varepsilon}$
and
$y>a_{\varepsilon}$
and
![]() $x>a_{\varepsilon}$
,
$x>a_{\varepsilon}$
,
which is occasionally called Potter’s bound.
Lemma 2.2.
There exists
![]() $c_0>0$
such that, for any
$c_0>0$
such that, for any
![]() $s>0$
and
$s>0$
and
![]() $x>2+2a_{0.5}$
,
$x>2+2a_{0.5}$
,
![]() $G_s(x)\,:\!=\,{\rm P}(|\xi_s|>x)\le c_0 s x^{-\alpha}L(x)$
.
$G_s(x)\,:\!=\,{\rm P}(|\xi_s|>x)\le c_0 s x^{-\alpha}L(x)$
.
Proof. By [Reference Durrett24, (3.3.1)], for any
![]() $x>2$
,
$x>2$
,
where in the last equality we used the symmetry of
![]() $\|\psi(\theta)\|$
. By (H2), it is clear that there exists
$\|\psi(\theta)\|$
. By (H2), it is clear that there exists
![]() $c_1>0$
such that
$c_1>0$
such that
![]() $\|\psi(\theta)\| \le c_1\theta^{\alpha}L\big(\theta^{-1}\big)$
,
$\|\psi(\theta)\| \le c_1\theta^{\alpha}L\big(\theta^{-1}\big)$
,
![]() $|\theta|\le 1$
. Thus, for
$|\theta|\le 1$
. Thus, for
![]() $x>2+2a_{0.5}$
, using (2.2) with
$x>2+2a_{0.5}$
, using (2.2) with
![]() $\varepsilon=0.5$
, we get
$\varepsilon=0.5$
, we get
The proof is now complete.
Remark 2.1. It follows from Lemma 2.1 that
![]() $\lim_{t\to\infty}{\textrm{e}}^{\lambda t}{\rm P}(|\xi_s|\ge h_t) = s({q_1+q_2})/{\alpha}$
, which implies that
$\lim_{t\to\infty}{\textrm{e}}^{\lambda t}{\rm P}(|\xi_s|\ge h_t) = s({q_1+q_2})/{\alpha}$
, which implies that
![]() ${\rm P}(|\xi_s|\ge x) \sim (({q_1+q_2})/{\alpha})sx^{-\alpha}L(x)$
,
${\rm P}(|\xi_s|\ge x) \sim (({q_1+q_2})/{\alpha})sx^{-\alpha}L(x)$
,
![]() $x\to\infty$
.
$x\to\infty$
.
Now we recall the many-to-one formula which is useful in computing expectations. We only list some special cases that we use here; see [Reference Hardy and Harris26, Theorem 8.5] for general cases.
Recall that, for any
![]() $u\in\mathbb{T}$
,
$u\in\mathbb{T}$
,
![]() $n^u$
is the number of particles in
$n^u$
is the number of particles in
![]() $I_u\setminus \{o\}$
.
$I_u\setminus \{o\}$
.
Lemma 2.3. (Many-to-one formula.) Let
![]() $\{n_t\}$
be a Poisson process with parameter
$\{n_t\}$
be a Poisson process with parameter
![]() $\beta$
on some probability space
$\beta$
on some probability space
![]() $(\Omega,{\mathcal{G}},P)$
. Then, for any
$(\Omega,{\mathcal{G}},P)$
. Then, for any
![]() $g\in\mathcal{B}_\textrm{b}^+(\mathbb{R})$
,
$g\in\mathcal{B}_\textrm{b}^+(\mathbb{R})$
,
![]() $\mathbb{E}\big(\sum_{v\in\mathcal{L}_t}g(n^v)\big) = {\textrm{e}}^{\lambda t}E(g(n_t))$
and, for any
$\mathbb{E}\big(\sum_{v\in\mathcal{L}_t}g(n^v)\big) = {\textrm{e}}^{\lambda t}E(g(n_t))$
and, for any
![]() $0\le s< t$
,
$0\le s< t$
,
![]() $\mathbb{E}\big(\sum_{v\in\mathcal{L}_t}{\textbf{1}}_{b_v\le t-s}\big) = {\textrm{e}}^{\lambda t}P(n_t-n_{t-s}=0) = {\textrm{e}}^{\lambda t}{\textrm{e}}^{-\beta s}$
.
$\mathbb{E}\big(\sum_{v\in\mathcal{L}_t}{\textbf{1}}_{b_v\le t-s}\big) = {\textrm{e}}^{\lambda t}P(n_t-n_{t-s}=0) = {\textrm{e}}^{\lambda t}{\textrm{e}}^{-\beta s}$
.
2.2. Proof of the Theorem 1.1
Recall that, on some extension
![]() $(\Omega, {\mathcal{G}}, P)$
of the probability space on which the branching Lévy process is defined, given W,
$(\Omega, {\mathcal{G}}, P)$
of the probability space on which the branching Lévy process is defined, given W,
![]() $\sum_{j}\delta_{e_j}$
is a Poisson random measure with intensity
$\sum_{j}\delta_{e_j}$
is a Poisson random measure with intensity
![]() $\vartheta Wv_\alpha({\textrm{d}} x)$
,
$\vartheta Wv_\alpha({\textrm{d}} x)$
,
![]() $\{T_j, j\ge 1\}$
is a sequence of i.i.d. random variables with common law
$\{T_j, j\ge 1\}$
is a sequence of i.i.d. random variables with common law
where
![]() $\vartheta=\int_0^\infty{\textrm{e}}^{-\lambda r}\mathbb{P}(Z_r>0)\,{\rm d}r$
, and
$\vartheta=\int_0^\infty{\textrm{e}}^{-\lambda r}\mathbb{P}(Z_r>0)\,{\rm d}r$
, and
![]() $\sum_{j}\delta_{e_j}$
and
$\sum_{j}\delta_{e_j}$
and
![]() $\{T_j, j\ge 1\}$
are independent.
$\{T_j, j\ge 1\}$
are independent.
Lemma 2.4.
Let
![]() $\mathcal{N}_\infty=\sum_{j}T_j\delta_{e_j}$
. Then
$\mathcal{N}_\infty=\sum_{j}T_j\delta_{e_j}$
. Then
![]() $\mathcal{N}_\infty\in\mathcal{M}\big(\overline{\mathbb{R}}_0\big)$
and the Laplace transform of
$\mathcal{N}_\infty\in\mathcal{M}\big(\overline{\mathbb{R}}_0\big)$
and the Laplace transform of
![]() $\mathcal{N}_\infty$
is given by
$\mathcal{N}_\infty$
is given by
Proof. First note that, for any
![]() $a>0$
,
$a>0$
,
![]() $\vartheta Wv_\alpha([{-}\infty,-a]\cup [a,\infty])<\infty$
,
$\vartheta Wv_\alpha([{-}\infty,-a]\cup [a,\infty])<\infty$
,
![]() $\mathbb{P} $
-a.s. Thus, given W,
$\mathbb{P} $
-a.s. Thus, given W,
![]() $\sum_{j}{\textbf{1}}_{|e_j|\ge a}$
is Poisson distributed with parameter
$\sum_{j}{\textbf{1}}_{|e_j|\ge a}$
is Poisson distributed with parameter
![]() $\vartheta Wv_\alpha([{-}\infty,-a]\cup [a,\infty])$
, which implies that
$\vartheta Wv_\alpha([{-}\infty,-a]\cup [a,\infty])$
, which implies that
![]() $\sum_{j}{\textbf{1}}_{|e_j|\ge a}<\infty$
, a.s. Thus, by the definition of
$\sum_{j}{\textbf{1}}_{|e_j|\ge a}<\infty$
, a.s. Thus, by the definition of
![]() $\mathcal{N}_\infty$
,
$\mathcal{N}_\infty$
,
 $$ P(\mathcal{N}_\infty([{-}\infty,-a]\cup [a,\infty])<\infty) = P\Bigg(\sum_{j}{\textbf{1}}_{|e_j|\ge a}<\infty\Bigg) = 1. $$
$$ P(\mathcal{N}_\infty([{-}\infty,-a]\cup [a,\infty])<\infty) = P\Bigg(\sum_{j}{\textbf{1}}_{|e_j|\ge a}<\infty\Bigg) = 1. $$
So
![]() $\mathcal{N}_\infty\in\mathcal{M}\big(\overline{\mathbb{R}}_0\big)$
. Note that
$\mathcal{N}_\infty\in\mathcal{M}\big(\overline{\mathbb{R}}_0\big)$
. Note that
 \begin{align*} \phi(\theta) \,:\!=\, E\big({\textrm{e}}^{-\theta T_j}\big) & = \vartheta^{-1}\sum_{k\ge 1}{\textrm{e}}^{-\theta k}\int_0^\infty{\textrm{e}}^{-\lambda r}\mathbb{P}(Z_r=k)\,{\rm d}r \\ & = \vartheta^{-1}\int_0^\infty{\textrm{e}}^{-\lambda r}\mathbb{E}\big({\textrm{e}}^{-\theta Z_r},Z_r>0\big)\,{\rm d}r \\ & = 1 - \vartheta^{-1}\int_0^\infty{\textrm{e}}^{-\lambda r}\mathbb{E}\big(1-{\textrm{e}}^{-\theta Z_r}\big)\,{\rm d}r. \end{align*}
\begin{align*} \phi(\theta) \,:\!=\, E\big({\textrm{e}}^{-\theta T_j}\big) & = \vartheta^{-1}\sum_{k\ge 1}{\textrm{e}}^{-\theta k}\int_0^\infty{\textrm{e}}^{-\lambda r}\mathbb{P}(Z_r=k)\,{\rm d}r \\ & = \vartheta^{-1}\int_0^\infty{\textrm{e}}^{-\lambda r}\mathbb{E}\big({\textrm{e}}^{-\theta Z_r},Z_r>0\big)\,{\rm d}r \\ & = 1 - \vartheta^{-1}\int_0^\infty{\textrm{e}}^{-\lambda r}\mathbb{E}\big(1-{\textrm{e}}^{-\theta Z_r}\big)\,{\rm d}r. \end{align*}
Thus, for any
![]() $g\in C_\textrm{c}^+\big(\overline{\mathbb{R}}_0\big)$
,
$g\in C_\textrm{c}^+\big(\overline{\mathbb{R}}_0\big)$
,
 \begin{align*} E\big({\textrm{e}}^{-\mathcal{N}_\infty(g)}\big) = E\big({\textrm{e}}^{-\sum_j T_j g(e_j)}\big) & = E\Bigg(\prod_j \phi(g(e_j))\Bigg) \\ & = \mathbb{E}\bigg(\exp\bigg\{{-}\vartheta W\int_{\mathbb{R}_0}(1-\phi(g(x)))\,v_\alpha({\rm d}x)\bigg\}\bigg) \\ & = \mathbb{E}\bigg(\exp\bigg\{{-}W\int_0^\infty{\textrm{e}}^{-\lambda r}\int_{\mathbb{R}_0} \mathbb{E}\big(1-{\textrm{e}}^{-Z_{r} g(x)}\big)\,v_\alpha({\rm d}x)\,{\rm d}r\bigg\}\bigg). \end{align*}
\begin{align*} E\big({\textrm{e}}^{-\mathcal{N}_\infty(g)}\big) = E\big({\textrm{e}}^{-\sum_j T_j g(e_j)}\big) & = E\Bigg(\prod_j \phi(g(e_j))\Bigg) \\ & = \mathbb{E}\bigg(\exp\bigg\{{-}\vartheta W\int_{\mathbb{R}_0}(1-\phi(g(x)))\,v_\alpha({\rm d}x)\bigg\}\bigg) \\ & = \mathbb{E}\bigg(\exp\bigg\{{-}W\int_0^\infty{\textrm{e}}^{-\lambda r}\int_{\mathbb{R}_0} \mathbb{E}\big(1-{\textrm{e}}^{-Z_{r} g(x)}\big)\,v_\alpha({\rm d}x)\,{\rm d}r\bigg\}\bigg). \end{align*}
The proof is now complete.
To prove Theorem 1.1 we use the idea of ‘one large jump’, which has been used in [Reference Bhattacharya, Hazra and Roy8, Reference Bhattacharya, Hazra and Roy9, Reference Durrett23] for branching random walks. By ‘one large jump’ we mean that with large probability, for all
![]() $v \in \mathcal{L}_t$
, at most one of the random variables
$v \in \mathcal{L}_t$
, at most one of the random variables
![]() $\{|X_{u,t}| \,:\, u \in I_v\}$
is bigger than
$\{|X_{u,t}| \,:\, u \in I_v\}$
is bigger than
![]() $h_t\theta/t$
(
$h_t\theta/t$
(
![]() $\theta>0$
). Thus, by (1.1), to investigate the limit property of
$\theta>0$
). Thus, by (1.1), to investigate the limit property of
![]() $\mathcal{N}_t$
defined by (1.9), we consider the limit of the point process defined by
$\mathcal{N}_t$
defined by (1.9), we consider the limit of the point process defined by
![]() $\widetilde{\mathcal{N}}_t \,:\!=\, \sum_{v\in\mathcal{L}_t}\sum_{u\in I_v}\delta_{h_t^{-1}X_{u,t}}$
.
$\widetilde{\mathcal{N}}_t \,:\!=\, \sum_{v\in\mathcal{L}_t}\sum_{u\in I_v}\delta_{h_t^{-1}X_{u,t}}$
.
Proposition 2.1.
Under
![]() $\mathbb{P}$
, as
$\mathbb{P}$
, as
![]() $t\to\infty$
,
$t\to\infty$
,
![]() $\widetilde{\mathcal{N}}_t\overset{\textrm{d}}{\to}\mathcal{N}_\infty$
.
$\widetilde{\mathcal{N}}_t\overset{\textrm{d}}{\to}\mathcal{N}_\infty$
.
The proof of this proposition is postponed to the next subsection. The following lemma formalizes the well-known one large jump principle (see, e.g., Steps 3 and 4 in [Reference Durrett23, Section 2]) at the level of point processes. Because of Lemma 2.5, it suffices to investigate the weak convergence of
![]() $\widetilde{\mathcal{N}}_t$
, which is much easier compared to that of
$\widetilde{\mathcal{N}}_t$
, which is much easier compared to that of
![]() ${\mathcal{N}}_t$
.
${\mathcal{N}}_t$
.
Lemma 2.5.
Assume
![]() $g \in C_\textrm{c}^+\big(\overline{\mathbb{R}}_0\big)$
. For any
$g \in C_\textrm{c}^+\big(\overline{\mathbb{R}}_0\big)$
. For any
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
![]() $\lim_{t\to\infty}\mathbb{P}(|\mathcal{N}_t(g)-\widetilde{\mathcal{N}}_t(g)|>\varepsilon)=0$
.
$\lim_{t\to\infty}\mathbb{P}(|\mathcal{N}_t(g)-\widetilde{\mathcal{N}}_t(g)|>\varepsilon)=0$
.
Proof. Since
![]() $g \in C_\textrm{c}^+\big(\overline{\mathbb{R}}_0\big)$
, we have Supp
$g \in C_\textrm{c}^+\big(\overline{\mathbb{R}}_0\big)$
, we have Supp
![]() $(g) \subset \{x \,:\, |x|> \delta\}$
for some
$(g) \subset \{x \,:\, |x|> \delta\}$
for some
![]() $\delta> 0$
.
$\delta> 0$
.
Step 1: For any
![]() $\theta > 0$
, let
$\theta > 0$
, let
![]() $A_t(\theta)$
denote the event that, for all
$A_t(\theta)$
denote the event that, for all
![]() $v \in \mathcal{L}_t$
, at most one of the random variables
$v \in \mathcal{L}_t$
, at most one of the random variables
![]() $\{|X_{u,t}| \,:\, u \in I_v\}$
is bigger than
$\{|X_{u,t}| \,:\, u \in I_v\}$
is bigger than
![]() $h_t\theta/t$
. We claim that
$h_t\theta/t$
. We claim that
Note that
 \begin{align} \mathbb{P}\Big(A_t(\theta)^\textrm{c}\mid\mathcal{F}_t^\mathbb{T}\Big) \le \sum_{v\in\mathcal{L}_t}\mathbb{P} \Bigg(\sum_{u\in I_v}{\textbf{1}}_{\{|X_{u,t}|>h_t\theta/t\}} \ge 2 \mid \mathcal{F}_t^\mathbb{T}\Bigg). \end{align}
\begin{align} \mathbb{P}\Big(A_t(\theta)^\textrm{c}\mid\mathcal{F}_t^\mathbb{T}\Big) \le \sum_{v\in\mathcal{L}_t}\mathbb{P} \Bigg(\sum_{u\in I_v}{\textbf{1}}_{\{|X_{u,t}|>h_t\theta/t\}} \ge 2 \mid \mathcal{F}_t^\mathbb{T}\Bigg). \end{align}
By Lemma 2.2 and (2.2) with
![]() $\varepsilon=0.5$
, we have, for
$\varepsilon=0.5$
, we have, for
![]() $h_t\theta/t>2+2a_{0.5}$
and
$h_t\theta/t>2+2a_{0.5}$
and
![]() $h_t>a_{0.5}$
,
$h_t>a_{0.5}$
,
 \begin{align} \mathbb{P}\Big(|X_{u,t}|>h_t\theta/t \mid \mathcal{F}_t^\mathbb{T}\Big) & = {\rm P}(|\xi_s|>h_t\theta/t)|_{s=\tau_{u,t}} \nonumber \\ & \le c_0 \tau_{u,t} h_t^{-\alpha}t^\alpha\theta^{-\alpha}L(h_t\theta/t) \nonumber \\ & \le 2c_0 \theta^{-\alpha} t^{1+\alpha} h_t^{-\alpha}L(h_t)\big[(\theta/t)^{1/2}+(\theta/t)^{-1/2}\big] \,:\!=\, p_t. \end{align}
\begin{align} \mathbb{P}\Big(|X_{u,t}|>h_t\theta/t \mid \mathcal{F}_t^\mathbb{T}\Big) & = {\rm P}(|\xi_s|>h_t\theta/t)|_{s=\tau_{u,t}} \nonumber \\ & \le c_0 \tau_{u,t} h_t^{-\alpha}t^\alpha\theta^{-\alpha}L(h_t\theta/t) \nonumber \\ & \le 2c_0 \theta^{-\alpha} t^{1+\alpha} h_t^{-\alpha}L(h_t)\big[(\theta/t)^{1/2}+(\theta/t)^{-1/2}\big] \,:\!=\, p_t. \end{align}
Recall that the number of elements in
![]() $I_v$
is
$I_v$
is
![]() $n^v+1$
. Since they are conditioned on
$n^v+1$
. Since they are conditioned on
![]() $\mathcal{F}_t^\mathbb{T}$
, the
$\mathcal{F}_t^\mathbb{T}$
, the
![]() $\{X_{u,t}, u\in I_v\}$
are independent, and by (2.5) we get
$\{X_{u,t}, u\in I_v\}$
are independent, and by (2.5) we get
 \begin{align*} \mathbb{P}\Bigg(\sum_{u\in I_v}{\textbf{1}}_{\{|X_{u,t}|>h_t\theta/t\}}\ge 2 \mid \mathcal{F}_t^\mathbb{T}\Bigg) & \le \sum_{m=2}^{n^v+1}\left(\begin{array}{c}n^v+1\\m\end{array}\right)p_t^m \\ & = p_t^2\sum_{m=0}^{n^v-1}\left(\begin{array}{c}n^v+1\\m+2\end{array}\right) p_t^m \\ & \le p_t^2\sum_{m=0}^{n^v-1} n^v(n^v+1)\left(\begin{array}{c}n^v-1\\m\end{array}\right) p_t^m \\ & = p_t^2 n^v(n^v+1)(1+p_t)^{n^v-1}. \end{align*}
\begin{align*} \mathbb{P}\Bigg(\sum_{u\in I_v}{\textbf{1}}_{\{|X_{u,t}|>h_t\theta/t\}}\ge 2 \mid \mathcal{F}_t^\mathbb{T}\Bigg) & \le \sum_{m=2}^{n^v+1}\left(\begin{array}{c}n^v+1\\m\end{array}\right)p_t^m \\ & = p_t^2\sum_{m=0}^{n^v-1}\left(\begin{array}{c}n^v+1\\m+2\end{array}\right) p_t^m \\ & \le p_t^2\sum_{m=0}^{n^v-1} n^v(n^v+1)\left(\begin{array}{c}n^v-1\\m\end{array}\right) p_t^m \\ & = p_t^2 n^v(n^v+1)(1+p_t)^{n^v-1}. \end{align*}
Thus, by (2.4) and the many-to-one formula (Lemma 2.3),
 \begin{align} \mathbb{P}\big(A_t(\theta)^\textrm{c}\big) = \mathbb{E}\big(\mathbb{P}\big(A_t(\theta)^\textrm{c}\mid\mathcal{F}_t^\mathbb{T}\big)\big) & \le {\textrm{e}}^{\lambda t}p_t^2E\big(n_t(n_t+1)(1+p_t)^{n_t-1}\big) \nonumber \\ & = {\textrm{e}}^{\lambda t} p_t^2\big(2\beta+(1+p_t)\beta^2\big){\textrm{e}}^{\beta p_t}, \end{align}
\begin{align} \mathbb{P}\big(A_t(\theta)^\textrm{c}\big) = \mathbb{E}\big(\mathbb{P}\big(A_t(\theta)^\textrm{c}\mid\mathcal{F}_t^\mathbb{T}\big)\big) & \le {\textrm{e}}^{\lambda t}p_t^2E\big(n_t(n_t+1)(1+p_t)^{n_t-1}\big) \nonumber \\ & = {\textrm{e}}^{\lambda t} p_t^2\big(2\beta+(1+p_t)\beta^2\big){\textrm{e}}^{\beta p_t}, \end{align}
where
![]() $n_t$
is a Poisson process with parameter
$n_t$
is a Poisson process with parameter
![]() $\beta$
on some probability space
$\beta$
on some probability space
![]() $(\Omega, {\mathcal{G}}, P)$
. Since
$(\Omega, {\mathcal{G}}, P)$
. Since
![]() ${\textrm{e}}^{\lambda t}h_t^{-\alpha}L(h_t)\to1$
, (2.3) follows immediately from (2.5) and (2.6).
${\textrm{e}}^{\lambda t}h_t^{-\alpha}L(h_t)\to1$
, (2.3) follows immediately from (2.5) and (2.6).
Step 2: Let
![]() $\varrho>\beta+1$
, to be chosen later. Let
$\varrho>\beta+1$
, to be chosen later. Let
![]() $B_t(\varrho)$
be the event that, for all
$B_t(\varrho)$
be the event that, for all
![]() $v \in \mathcal{L}_t$
,
$v \in \mathcal{L}_t$
,
![]() $n_t^v\le \varrho t$
. Using the many-to-one formula,
$n_t^v\le \varrho t$
. Using the many-to-one formula,
 \begin{align*} \mathbb{P}\big(B_t(\varrho)^\textrm{c}\big) \le \mathbb{E}\Bigg(\sum_{v\in\mathcal{L}_t}{\textbf{1}}_{n^v>\varrho t}\Bigg) & = {\textrm{e}}^{\lambda t}P(n_t>\varrho t) \\ & \le {\textrm{e}}^{\lambda t} \inf_{r>0}{\textrm{e}}^{-r \varrho t}E\big({\textrm{e}}^{r n _t}\big) \\ & = {\textrm{e}}^{\lambda t} \inf_{r>0}\exp\big\{\big(\big({\textrm{e}}^r-1\big)\beta-r\varrho\big)t\big\} \\ & = {\textrm{e}}^{\lambda t}\exp\{{-}(\varrho(\log\varrho-\log\beta)-\varrho+\beta) t\}. \end{align*}
\begin{align*} \mathbb{P}\big(B_t(\varrho)^\textrm{c}\big) \le \mathbb{E}\Bigg(\sum_{v\in\mathcal{L}_t}{\textbf{1}}_{n^v>\varrho t}\Bigg) & = {\textrm{e}}^{\lambda t}P(n_t>\varrho t) \\ & \le {\textrm{e}}^{\lambda t} \inf_{r>0}{\textrm{e}}^{-r \varrho t}E\big({\textrm{e}}^{r n _t}\big) \\ & = {\textrm{e}}^{\lambda t} \inf_{r>0}\exp\big\{\big(\big({\textrm{e}}^r-1\big)\beta-r\varrho\big)t\big\} \\ & = {\textrm{e}}^{\lambda t}\exp\{{-}(\varrho(\log\varrho-\log\beta)-\varrho+\beta) t\}. \end{align*}
Choose
![]() $\varrho$
large enough that
$\varrho$
large enough that
![]() $\varrho(\log \varrho-\log \beta)-\varrho+\beta>\lambda$
; then
$\varrho(\log \varrho-\log \beta)-\varrho+\beta>\lambda$
; then
![]() $\lim_{t\to\infty}\mathbb{P}\big(B_t(\varrho)^\textrm{c}\big) = 0$
.
$\lim_{t\to\infty}\mathbb{P}\big(B_t(\varrho)^\textrm{c}\big) = 0$
.
Step 3: Since
![]() $g\in C_\textrm{c}^+\big(\overline{\mathbb{R}}_0\big)$
, g is uniformly continuous, i.e. for any
$g\in C_\textrm{c}^+\big(\overline{\mathbb{R}}_0\big)$
, g is uniformly continuous, i.e. for any
![]() $a>0$
there exists
$a>0$
there exists
![]() $\eta>0$
such that
$\eta>0$
such that
![]() $|g(x_1)-g(x_2)|\le a$
whenever
$|g(x_1)-g(x_2)|\le a$
whenever
![]() $|x_1-x_2|<\eta$
.
$|x_1-x_2|<\eta$
.
Now consider
![]() $\theta$
small enough that
$\theta$
small enough that
![]() $\varrho\theta<\eta\wedge(\delta/2)$
. Let
$\varrho\theta<\eta\wedge(\delta/2)$
. Let
![]() $v^{\prime}\in I_v$
be such that
$v^{\prime}\in I_v$
be such that
![]() $|X_{v^{\prime},t}|=\max_{u\in I_v}\{|X_{u,t}|\}$
. We note that, on the event
$|X_{v^{\prime},t}|=\max_{u\in I_v}\{|X_{u,t}|\}$
. We note that, on the event
![]() $A_t(\theta)$
,
$A_t(\theta)$
,
![]() $|X_{u,t}|\le \theta h_t/t\le h_t\delta/2$
for any
$|X_{u,t}|\le \theta h_t/t\le h_t\delta/2$
for any
![]() $u\in I_v\setminus\{v^{\prime}\}$
and
$u\in I_v\setminus\{v^{\prime}\}$
and
![]() $t>1$
, and thus
$t>1$
, and thus
![]() $g(X_{u,t}/h_t)=0$
, which implies that
$g(X_{u,t}/h_t)=0$
, which implies that
Thus it follows that, on the event
![]() $A_t(\theta)$
,
$A_t(\theta)$
,
 \begin{equation} \big|\mathcal{N}_t(g)-\widetilde{\mathcal{N}}_t(g)\big| = \Bigg|\sum_{v\in \mathcal{L}_t}\big[g\big(\xi^v_t/h_t\big)-g\big(X_{v^{\prime},t}/h_t\big)\big]\Bigg|. \end{equation}
\begin{equation} \big|\mathcal{N}_t(g)-\widetilde{\mathcal{N}}_t(g)\big| = \Bigg|\sum_{v\in \mathcal{L}_t}\big[g\big(\xi^v_t/h_t\big)-g\big(X_{v^{\prime},t}/h_t\big)\big]\Bigg|. \end{equation}
Since
![]() $\xi^v_t=\sum_{u\in I_v}X_{u,t}$
, on the event
$\xi^v_t=\sum_{u\in I_v}X_{u,t}$
, on the event
![]() $A_t(\theta)\cap B_t(\varrho)$
we have
$A_t(\theta)\cap B_t(\varrho)$
we have
 $$ h_t^{-1}|\xi_t^v-X_{v^{\prime},t}| = h_t^{-1}\Bigg|\sum_{u\in I_v\setminus \{v^{\prime}\}} X_{u,t}\Bigg| \le \theta t^{-1} n^v \le \varrho \theta < \eta\wedge(\delta/2). $$
$$ h_t^{-1}|\xi_t^v-X_{v^{\prime},t}| = h_t^{-1}\Bigg|\sum_{u\in I_v\setminus \{v^{\prime}\}} X_{u,t}\Bigg| \le \theta t^{-1} n^v \le \varrho \theta < \eta\wedge(\delta/2). $$
Note that if
![]() $|X_{v^{\prime},t}/h_t|\le \delta/2$
, then
$|X_{v^{\prime},t}/h_t|\le \delta/2$
, then
![]() $|\xi_t^v|/h_t< \delta$
, which implies that
$|\xi_t^v|/h_t< \delta$
, which implies that
![]() $g\big(\xi^v_t/h_t\big)-g\big(X_{v^{\prime},t}/h_t\big)=0$
. Thus,
$g\big(\xi^v_t/h_t\big)-g\big(X_{v^{\prime},t}/h_t\big)=0$
. Thus,
It follows from this and (2.7) that, on the event
![]() $A_t(\theta)\cap B_t(\varrho)$
,
$A_t(\theta)\cap B_t(\varrho)$
,
 \begin{align*} \big|\mathcal{N}_t(g)-\widetilde{\mathcal{N}}_t(g)\big| & \le a\sum_{v\in \mathcal{L}_t }{\textbf{1}}_{\big\{\big|X_{v^{\prime},t}\big| >h_t\delta/2\big\}} \\ & \le a \sum_{v\in \mathcal{L}_t }\sum_{u\in I_v}{\textbf{1}}_{\big\{\big|X_{u,t}\big|> h_t\delta/2\big\}} = a \widetilde{\mathcal{N}}_t\{[{-}\infty,-\delta/2)\cup (\delta/2,\infty]\}. \end{align*}
\begin{align*} \big|\mathcal{N}_t(g)-\widetilde{\mathcal{N}}_t(g)\big| & \le a\sum_{v\in \mathcal{L}_t }{\textbf{1}}_{\big\{\big|X_{v^{\prime},t}\big| >h_t\delta/2\big\}} \\ & \le a \sum_{v\in \mathcal{L}_t }\sum_{u\in I_v}{\textbf{1}}_{\big\{\big|X_{u,t}\big|> h_t\delta/2\big\}} = a \widetilde{\mathcal{N}}_t\{[{-}\infty,-\delta/2)\cup (\delta/2,\infty]\}. \end{align*}
Let
![]() $f\in C_\textrm{c}^+\big(\overline{\mathbb{R}}_0\big)$
satisfy
$f\in C_\textrm{c}^+\big(\overline{\mathbb{R}}_0\big)$
satisfy
![]() $f(x)=1$
for
$f(x)=1$
for
![]() $|x|\ge \delta/2$
. Then
$|x|\ge \delta/2$
. Then
![]() $|\mathcal{N}_t(g)-\widetilde{\mathcal{N}}_t(g)|\le a\widetilde{\mathcal{N}}_t(f)$
.
$|\mathcal{N}_t(g)-\widetilde{\mathcal{N}}_t(g)|\le a\widetilde{\mathcal{N}}_t(f)$
.
Combining Steps 1–3, we get
 \begin{align*} \limsup_{t\to\infty}\mathbb{P}\big(\big|\mathcal{N}_t(g)-\widetilde{\mathcal{N}}_t(g)\big|>\varepsilon\big) & \le \limsup_{t\to\infty}\mathbb{P}\big(A_t(\theta)^\textrm{c}\big) + \mathbb{P}\big(B_t(\varrho)^\textrm{c}\big) + \mathbb{P}\big(\widetilde{\mathcal{N}}_t(f)>a^{-1}\varepsilon\big) \\ & = \limsup_{t\to\infty}\mathbb{P}\big(\widetilde{\mathcal{N}}_t(f)>a^{-1}\varepsilon\big) = P\big(\mathcal{N}_\infty(f)>a^{-1}\varepsilon\big), \end{align*}
\begin{align*} \limsup_{t\to\infty}\mathbb{P}\big(\big|\mathcal{N}_t(g)-\widetilde{\mathcal{N}}_t(g)\big|>\varepsilon\big) & \le \limsup_{t\to\infty}\mathbb{P}\big(A_t(\theta)^\textrm{c}\big) + \mathbb{P}\big(B_t(\varrho)^\textrm{c}\big) + \mathbb{P}\big(\widetilde{\mathcal{N}}_t(f)>a^{-1}\varepsilon\big) \\ & = \limsup_{t\to\infty}\mathbb{P}\big(\widetilde{\mathcal{N}}_t(f)>a^{-1}\varepsilon\big) = P\big(\mathcal{N}_\infty(f)>a^{-1}\varepsilon\big), \end{align*}
where the final equality follows from Proposition 2.1 (the proof of Proposition 2.1 does not use the result in this lemma). Then, letting
![]() $a\to0$
, we get the desired result.
$a\to0$
, we get the desired result.
Proof of Theorem 1.1. Using Lemma 2.4, Proposition 2.1, and Lemma 2.5, the results of Theorem 1.1 follow immediately.
2.3. Proof of Proposition 2.1
To prove the weak convergence of
![]() $\widetilde{\mathcal{N}}_t$
, we first cut the tree at time
$\widetilde{\mathcal{N}}_t$
, we first cut the tree at time
![]() $t-s$
. We divide the particles born before time t into two parts: the particles born before time
$t-s$
. We divide the particles born before time t into two parts: the particles born before time
![]() $t-s$
and after
$t-s$
and after
![]() $t-s$
. Define
$t-s$
. Define
Lemma 2.6.
For any
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $g \in C_\textrm{c}^+\big(\overline{\mathbb{R}}_0\big)$
,
$g \in C_\textrm{c}^+\big(\overline{\mathbb{R}}_0\big)$
,
![]() $\lim_{s\to\infty}\limsup_{t\to\infty} \mathbb{P}\big(\big|\widetilde{\mathcal{N}}_t(g)-\widetilde{\mathcal{N}}_{s,t}(g)\big|>\varepsilon\big)$
$\lim_{s\to\infty}\limsup_{t\to\infty} \mathbb{P}\big(\big|\widetilde{\mathcal{N}}_t(g)-\widetilde{\mathcal{N}}_{s,t}(g)\big|>\varepsilon\big)$
![]() $= 0$
.
$= 0$
.
Proof. Since
![]() $g \in C_\textrm{c}^+\big(\overline{\mathbb{R}}_0\big)$
, we have Supp
$g \in C_\textrm{c}^+\big(\overline{\mathbb{R}}_0\big)$
, we have Supp
![]() $(g)\subset\{x\,:\,|x|>\delta\}$
for some
$(g)\subset\{x\,:\,|x|>\delta\}$
for some
![]() $\delta > 0$
.
$\delta > 0$
.
Let
![]() $J_{s,t}$
be the event that, for all u with
$J_{s,t}$
be the event that, for all u with
![]() $b_u\le t-s$
,
$b_u\le t-s$
,
![]() $|X_{u,t}|\le h_t \delta/2$
. On
$|X_{u,t}|\le h_t \delta/2$
. On
![]() $J_{s,t}$
,
$J_{s,t}$
,
![]() $\widetilde{\mathcal{N}}_t(g)-\widetilde{\mathcal{N}}_{s,t}(g)=0$
, and thus we only need to show that
$\widetilde{\mathcal{N}}_t(g)-\widetilde{\mathcal{N}}_{s,t}(g)=0$
, and thus we only need to show that
Recall that
![]() $G_s(x)\,:\!=\,{\rm P}(|\xi_s|>x)$
. By Lemma 2.2, for t large enough that
$G_s(x)\,:\!=\,{\rm P}(|\xi_s|>x)$
. By Lemma 2.2, for t large enough that
![]() $h_t\delta/2\ge 2+2a_{0.5}$
,
$h_t\delta/2\ge 2+2a_{0.5}$
,
 \begin{align} \mathbb{P}\big(J_{s,t}^\textrm{c}\big) = 1 - \mathbb{P}(J_{s,t}) & = 1 - \mathbb{E}\Bigg(\prod_{u:b_u\le t-s}\big(1-G_{\tau_{u,t}}(h_t\delta/2)\big)\Bigg) \nonumber \\ & \le \mathbb{E}\Bigg(\sum_{u:b_u\le t-s}G_{\tau_{u,t}}(h_t\delta/2)\Bigg) \nonumber \\ & \le c_0h_t^{-\alpha}(\delta/2)^{-\alpha}L(h_t\delta/2) \mathbb{E}\Bigg(\sum_{u:b_u\le t-s}\tau_{u,t}\Bigg). \end{align}
\begin{align} \mathbb{P}\big(J_{s,t}^\textrm{c}\big) = 1 - \mathbb{P}(J_{s,t}) & = 1 - \mathbb{E}\Bigg(\prod_{u:b_u\le t-s}\big(1-G_{\tau_{u,t}}(h_t\delta/2)\big)\Bigg) \nonumber \\ & \le \mathbb{E}\Bigg(\sum_{u:b_u\le t-s}G_{\tau_{u,t}}(h_t\delta/2)\Bigg) \nonumber \\ & \le c_0h_t^{-\alpha}(\delta/2)^{-\alpha}L(h_t\delta/2) \mathbb{E}\Bigg(\sum_{u:b_u\le t-s}\tau_{u,t}\Bigg). \end{align}
In the first inequality we used
![]() $1-\prod_{i=1}^n(1-x_i) \le \sum_{i=1}^n x_i$
,
$1-\prod_{i=1}^n(1-x_i) \le \sum_{i=1}^n x_i$
,
![]() $x_i\in(0,1)$
. By the definition of
$x_i\in(0,1)$
. By the definition of
![]() $\tau_{u,t}$
,
$\tau_{u,t}$
,
 \begin{align} \sum_{u:b_u\le t-s}\tau_{u,t} & = \sum_{u:b_u\le t-s}\int_0^t {\textbf{1}}_{(b_u,\sigma_u)}(r)\,{\rm d}r \nonumber \\ & = \int_0^{t-s}\sum_{u} {\textbf{1}}_{(b_u,\sigma_u)}(r)\,{\rm d}r + \int_{t-s}^t\sum_{u} {\textbf{1}}_{b_u<t-s,\sigma_u>r}\,{\rm d}r. \end{align}
\begin{align} \sum_{u:b_u\le t-s}\tau_{u,t} & = \sum_{u:b_u\le t-s}\int_0^t {\textbf{1}}_{(b_u,\sigma_u)}(r)\,{\rm d}r \nonumber \\ & = \int_0^{t-s}\sum_{u} {\textbf{1}}_{(b_u,\sigma_u)}(r)\,{\rm d}r + \int_{t-s}^t\sum_{u} {\textbf{1}}_{b_u<t-s,\sigma_u>r}\,{\rm d}r. \end{align}
For the first part, noting that
![]() $r\in(b_u,\sigma_u)$
is equivalent to
$r\in(b_u,\sigma_u)$
is equivalent to
![]() $u\in \mathcal{L}_r$
, we get
$u\in \mathcal{L}_r$
, we get
For the second part, using the many-to-one formula we have
 $$ \mathbb{E}\Bigg(\sum_{u} {\textbf{1}}_{b_u<t-s,\sigma_u>r}\Bigg) = \mathbb{E}\Bigg(\sum_{u\in \mathcal{L}_r} {\textbf{1}}_{b_u<t-s}\Bigg) = {\textrm{e}}^{\lambda r}{\textrm{e}}^{-\beta (r+s-t)}. $$
$$ \mathbb{E}\Bigg(\sum_{u} {\textbf{1}}_{b_u<t-s,\sigma_u>r}\Bigg) = \mathbb{E}\Bigg(\sum_{u\in \mathcal{L}_r} {\textbf{1}}_{b_u<t-s}\Bigg) = {\textrm{e}}^{\lambda r}{\textrm{e}}^{-\beta (r+s-t)}. $$
Thus,
Combining (2.11), (2.12), and (2.13),
Therefore, by (2.10),
It follows from (1.7) that
![]() $\lim_{t\to\infty}{\textrm{e}}^{\lambda t}h_t^{-\alpha}L(h_t\delta/2)=1$
. First letting
$\lim_{t\to\infty}{\textrm{e}}^{\lambda t}h_t^{-\alpha}L(h_t\delta/2)=1$
. First letting
![]() $t\to\infty$
and then
$t\to\infty$
and then
![]() $s\to\infty$
in (2.14), we get (2.9) immediately. The proof is now complete.
$s\to\infty$
in (2.14), we get (2.9) immediately. The proof is now complete.
Now we consider the weak convergence of
![]() $\widetilde{\mathcal{N}}_{{s,t}}$
. Recall the definition of
$\widetilde{\mathcal{N}}_{{s,t}}$
. Recall the definition of
![]() $\widetilde{\mathcal{N}}_{s,t}$
in (2.8). Note that the atoms of
$\widetilde{\mathcal{N}}_{s,t}$
in (2.8). Note that the atoms of
![]() $\widetilde{\mathcal{N}}_{s,t}$
are
$\widetilde{\mathcal{N}}_{s,t}$
are
![]() $\big\{h_t^{-1}X_{u,t}, t-s< b_u\le t\big\}$
. Thus
$\big\{h_t^{-1}X_{u,t}, t-s< b_u\le t\big\}$
. Thus
![]() $\widetilde{\mathcal{N}}_{s,t}=\sum_{u:t-s< b_u<t}Z^u_t \delta_{h_t^{-1}X_{u,t}}$
, where
$\widetilde{\mathcal{N}}_{s,t}=\sum_{u:t-s< b_u<t}Z^u_t \delta_{h_t^{-1}X_{u,t}}$
, where
![]() $Z_t^u$
is the number of offspring of u alive at time t. Using the tree structure, we can split all the particles born after
$Z_t^u$
is the number of offspring of u alive at time t. Using the tree structure, we can split all the particles born after
![]() $t-s$
according to the branches generated by the particles alive at
$t-s$
according to the branches generated by the particles alive at
![]() $t-s$
. More precisely,
$t-s$
. More precisely,
where, for
![]() $w\in\mathcal{L}_{t-s}$
,
$w\in\mathcal{L}_{t-s}$
,
![]() $D_t^w\,:\!=\,\{u\,:\, w\in I_u, t-s< b_u\le t\}$
is the set of all the offspring of w before time t. By the branching property,
$D_t^w\,:\!=\,\{u\,:\, w\in I_u, t-s< b_u\le t\}$
is the set of all the offspring of w before time t. By the branching property,
![]() $M_{s,t}^w$
are i.i.d. with a common law which is the same as that of
$M_{s,t}^w$
are i.i.d. with a common law which is the same as that of
![]() $M_{s,t}\,:\!=\,\sum_{u\in D_s }Z^u_{s}\delta_{h_t^{-1}X_{u,s}}$
, where
$M_{s,t}\,:\!=\,\sum_{u\in D_s }Z^u_{s}\delta_{h_t^{-1}X_{u,s}}$
, where
![]() $D_s=\{u\,:\, 0<b_u\le s\}$
.
$D_s=\{u\,:\, 0<b_u\le s\}$
.
Lemma 2.7.
For any
![]() $j=1,\ldots,n$
, let
$j=1,\ldots,n$
, let
![]() $\gamma_j(t)$
be a (0, 1]-valued function on
$\gamma_j(t)$
be a (0, 1]-valued function on
![]() $(0, \infty)$
. Suppose
$(0, \infty)$
. Suppose
![]() $a_t$
is a positive function with
$a_t$
is a positive function with
![]() $\lim_{t\to\infty}a_t=\infty$
such that
$\lim_{t\to\infty}a_t=\infty$
such that
![]() $\lim_{t\to\infty}a_t(1-\gamma_j(t))= c_j<\infty$
. Then
$\lim_{t\to\infty}a_t(1-\gamma_j(t))= c_j<\infty$
. Then
![]() $\lim_{t\to\infty}a_t\big(1-\prod_{j=1}^n \gamma_j(t)\big)= \sum_{j=1}^n c_j$
.
$\lim_{t\to\infty}a_t\big(1-\prod_{j=1}^n \gamma_j(t)\big)= \sum_{j=1}^n c_j$
.
Proof. Note that
![]() $1-\prod_{j=1}^n \gamma_j(t)=\sum_{j=1}^n\prod_{k=1}^{j-1}\gamma_{k}(t)(1-\gamma_j(t))$
. Since
$1-\prod_{j=1}^n \gamma_j(t)=\sum_{j=1}^n\prod_{k=1}^{j-1}\gamma_{k}(t)(1-\gamma_j(t))$
. Since
![]() $\gamma_j(t)\to 1$
we get that, as
$\gamma_j(t)\to 1$
we get that, as
![]() $t\to\infty$
,
$t\to\infty$
,
 \begin{equation*} a_t\Bigg(1-\prod_{j=1}^n \gamma_j(t)\Bigg) = \sum_{j=1}^n\prod_{k=1}^{j-1}\gamma_{k}(t) a_t(1-\gamma_j(t))\to \sum_{j=1}^n c_j. \end{equation*}
\begin{equation*} a_t\Bigg(1-\prod_{j=1}^n \gamma_j(t)\Bigg) = \sum_{j=1}^n\prod_{k=1}^{j-1}\gamma_{k}(t) a_t(1-\gamma_j(t))\to \sum_{j=1}^n c_j. \end{equation*}
Proof of Proposition 2.1. By Lemma 2.6, we only need to consider the convergence of
![]() $\widetilde{\mathcal{N}}_{s,t}$
. Assume that Supp
$\widetilde{\mathcal{N}}_{s,t}$
. Assume that Supp
![]() $(g)\subset\{x\,:\,|x|>\delta\}$
for some
$(g)\subset\{x\,:\,|x|>\delta\}$
for some
![]() $\delta > 0$
. Using the Markov property and the decomposition of
$\delta > 0$
. Using the Markov property and the decomposition of
![]() $\widetilde{\mathcal{N}}_{s,t}$
in (2.15), we have
$\widetilde{\mathcal{N}}_{s,t}$
in (2.15), we have
We claim that
 \begin{equation} \lim_{t\to\infty}\big(1-\mathbb{E}\big({\textrm{e}}^{-M_{s,t}(g)}\big)\big){\textrm{e}}^{\lambda t} = \int_{\mathbb{R}_0} \mathbb{E}\Bigg[\sum_{u\in D_s}\tau_{u,s}1-{\textrm{e}}^{-Z_s^u g(x)}\Bigg]\,v_\alpha({\rm d}x). \end{equation}
\begin{equation} \lim_{t\to\infty}\big(1-\mathbb{E}\big({\textrm{e}}^{-M_{s,t}(g)}\big)\big){\textrm{e}}^{\lambda t} = \int_{\mathbb{R}_0} \mathbb{E}\Bigg[\sum_{u\in D_s}\tau_{u,s}1-{\textrm{e}}^{-Z_s^u g(x)}\Bigg]\,v_\alpha({\rm d}x). \end{equation}
By the definition of
![]() $M_{s,t}$
, we have
$M_{s,t}$
, we have
 $$ \Big(1-\mathbb{E}\Big({\textrm{e}}^{-M_{s,t}(g)}\mid\mathcal{F}_s^\mathbb{T}\Big)\Big){\textrm{e}}^{\lambda t} = {\textrm{e}}^{\lambda t}\Bigg(1-\prod_{u\in D_s}\mathbb{E}\Big({\textrm{e}}^{-Z_{s}^ug\big(h_t^{-1}X_{u,s}\big)}\mid\mathcal{F}_s^\mathbb{T}\Big)\Bigg). $$
$$ \Big(1-\mathbb{E}\Big({\textrm{e}}^{-M_{s,t}(g)}\mid\mathcal{F}_s^\mathbb{T}\Big)\Big){\textrm{e}}^{\lambda t} = {\textrm{e}}^{\lambda t}\Bigg(1-\prod_{u\in D_s}\mathbb{E}\Big({\textrm{e}}^{-Z_{s}^ug\big(h_t^{-1}X_{u,s}\big)}\mid\mathcal{F}_s^\mathbb{T}\Big)\Bigg). $$
Note that, given
![]() $\mathcal{F}_s^\mathbb{T}$
,
$\mathcal{F}_s^\mathbb{T}$
,
![]() $X_{u,s}\overset{\textrm{d}}{=}\xi_{\tau_{u,s}}$
. Thus, by Lemma 2.1 (with s replaced by
$X_{u,s}\overset{\textrm{d}}{=}\xi_{\tau_{u,s}}$
. Thus, by Lemma 2.1 (with s replaced by
![]() $\tau_{u,s}$
and g replaced by
$\tau_{u,s}$
and g replaced by
![]() $1-{\textrm{e}}^{-Z^u_s g(x)}$
),
$1-{\textrm{e}}^{-Z^u_s g(x)}$
),
Hence, it follows from Lemma 2.7 that
Moreover, for
![]() $h_t\delta\ge 2+2a_{0.5}$
,
$h_t\delta\ge 2+2a_{0.5}$
,
 \begin{align} {\textrm{e}}^{\lambda t}\big(1-\mathbb{E}\big[{\textrm{e}}^{-M_{s,t}(g)}\mid\mathcal{F}_s^\mathbb{T}\big]\big) & \le {\textrm{e}}^{\lambda t}\mathbb{E}\big(M_{s,t}(g)\mid\mathcal{F}_s^\mathbb{T}\big) \nonumber \\ & \le \|g\|_\infty{\textrm{e}}^{\lambda t}\sum_{u\in D_s}Z_s^u G_{\tau_{u,s}}(h_t\delta) \nonumber \\ & \le c_0 \|g\|_\infty \delta^{-\alpha}{\textrm{e}}^{\lambda t}h_t^{-\alpha}L(h_t\delta)\sum_{u\in D_s}\tau_{u,s}Z_s^u \nonumber \\ & \le C\sum_{u\in D_s}\tau_{u,s}Z_s^u, \end{align}
\begin{align} {\textrm{e}}^{\lambda t}\big(1-\mathbb{E}\big[{\textrm{e}}^{-M_{s,t}(g)}\mid\mathcal{F}_s^\mathbb{T}\big]\big) & \le {\textrm{e}}^{\lambda t}\mathbb{E}\big(M_{s,t}(g)\mid\mathcal{F}_s^\mathbb{T}\big) \nonumber \\ & \le \|g\|_\infty{\textrm{e}}^{\lambda t}\sum_{u\in D_s}Z_s^u G_{\tau_{u,s}}(h_t\delta) \nonumber \\ & \le c_0 \|g\|_\infty \delta^{-\alpha}{\textrm{e}}^{\lambda t}h_t^{-\alpha}L(h_t\delta)\sum_{u\in D_s}\tau_{u,s}Z_s^u \nonumber \\ & \le C\sum_{u\in D_s}\tau_{u,s}Z_s^u, \end{align}
where C is a constant not depending on t. The third inequality follows from Lemma 2.2, and the final inequality from the fact that
![]() ${\textrm{e}}^{\lambda t}h_t^{-\alpha}L(h_t\delta)\to 1$
. Since
${\textrm{e}}^{\lambda t}h_t^{-\alpha}L(h_t\delta)\to 1$
. Since
![]() $\tau_{u,s}=\int_0^s{\textbf{1}}_{(b_u,\sigma_u)}(r)\,{\rm d}r$
,
$\tau_{u,s}=\int_0^s{\textbf{1}}_{(b_u,\sigma_u)}(r)\,{\rm d}r$
,
 \begin{align*} \mathbb{E}\Bigg(\sum_{u\in D_s}\tau_{u,s}Z_s^u\Bigg) & = \int_0^s\mathbb{E}\Bigg(\sum_{u\in D_s} {\textbf{1}}_{(b_u,\sigma_u)}(r) Z^u_s\Bigg)\,{\rm d}r \\ & = \int_0^s\mathbb{E}\Bigg(\sum_{u\in\mathcal{L}_r-\{o\}}Z^u_s\Bigg)\,{\rm d}r \le \int_0^s \mathbb{E} (Z_s)\,{\rm d}r = s{\textrm{e}}^{\lambda s}<\infty. \end{align*}
\begin{align*} \mathbb{E}\Bigg(\sum_{u\in D_s}\tau_{u,s}Z_s^u\Bigg) & = \int_0^s\mathbb{E}\Bigg(\sum_{u\in D_s} {\textbf{1}}_{(b_u,\sigma_u)}(r) Z^u_s\Bigg)\,{\rm d}r \\ & = \int_0^s\mathbb{E}\Bigg(\sum_{u\in\mathcal{L}_r-\{o\}}Z^u_s\Bigg)\,{\rm d}r \le \int_0^s \mathbb{E} (Z_s)\,{\rm d}r = s{\textrm{e}}^{\lambda s}<\infty. \end{align*}
Thus, by (2.18), (2.19), and the dominated convergence theorem, the claim (2.17) holds.
By (2.17) and the fact that
![]() $\lim_{t\to\infty}{\textrm{e}}^{-\lambda t}Z_{t-s}={\textrm{e}}^{-\lambda s}W$
, we have
$\lim_{t\to\infty}{\textrm{e}}^{-\lambda t}Z_{t-s}={\textrm{e}}^{-\lambda s}W$
, we have
 $$ \lim_{t\to\infty}\big[\mathbb{E}\big({\textrm{e}}^{-M_{s,t}(g)}\big)\big]^{Z_{t-s}} = \exp\Bigg\{{-}{\textrm{e}}^{-\lambda s}W\int_{\mathbb{R}_0} \mathbb{E}\Bigg[\sum_{u\in D_s}\tau_{u,s}\big(1-{\textrm{e}}^{-Z_s^u g(x)}\big)\Bigg]\,v_\alpha({\rm d}x)\Bigg\}. $$
$$ \lim_{t\to\infty}\big[\mathbb{E}\big({\textrm{e}}^{-M_{s,t}(g)}\big)\big]^{Z_{t-s}} = \exp\Bigg\{{-}{\textrm{e}}^{-\lambda s}W\int_{\mathbb{R}_0} \mathbb{E}\Bigg[\sum_{u\in D_s}\tau_{u,s}\big(1-{\textrm{e}}^{-Z_s^u g(x)}\big)\Bigg]\,v_\alpha({\rm d}x)\Bigg\}. $$
Thus, by (2.16) and the bounded convergence theorem,
 $$ \lim_{t\to\infty}\mathbb{E}\big({\textrm{e}}^{-\widetilde{\mathcal{N}}_{s,t}(g)}\big) = \mathbb{E}\Bigg(\exp\Bigg\{{-}{\textrm{e}}^{-\lambda s}W\int_{\mathbb{R}_0} \mathbb{E}\Bigg[\sum_{u\in D_s}\tau_{u,s}\big(1-{\textrm{e}}^{-Z_s^u g(x)}\big)\Bigg]\,v_\alpha({\rm d}x)\Bigg\}\Bigg). $$
$$ \lim_{t\to\infty}\mathbb{E}\big({\textrm{e}}^{-\widetilde{\mathcal{N}}_{s,t}(g)}\big) = \mathbb{E}\Bigg(\exp\Bigg\{{-}{\textrm{e}}^{-\lambda s}W\int_{\mathbb{R}_0} \mathbb{E}\Bigg[\sum_{u\in D_s}\tau_{u,s}\big(1-{\textrm{e}}^{-Z_s^u g(x)}\big)\Bigg]\,v_\alpha({\rm d}x)\Bigg\}\Bigg). $$
By the definition of
![]() $\tau_{u,s}$
, we have
$\tau_{u,s}$
, we have
Using the Markov property and the branching property, the
![]() $Z^u_s$
,
$Z^u_s$
,
![]() $u\in \mathcal{L}_r$
, are i.i.d. with the same distribution as
$u\in \mathcal{L}_r$
, are i.i.d. with the same distribution as
![]() $Z_{s-r}$
, and independent of
$Z_{s-r}$
, and independent of
![]() $\mathcal{L}_r$
. Thus,
$\mathcal{L}_r$
. Thus,
 \begin{align*} \mathbb{E}\sum_{u\in D_s}\tau_{u,s}\big(1-{\textrm{e}}^{-Z_s^u g(x)}\big) & = \int_0^s\mathbb{E}\big(Z_r-{\textbf{1}}_{\{o\in\mathcal{L}_r\}}\big)\mathbb{E}\big(1-{\textrm{e}}^{-Z_{s-r}g(x)}\big)\,{\rm d}r \\ & = \int_0^s\big({\textrm{e}}^{\lambda r}-{\textrm{e}}^{-\beta r}\big)\mathbb{E}\big(1-{\textrm{e}}^{-Z_{s-r} g(x)}\big)\,{\rm d}r, \end{align*}
\begin{align*} \mathbb{E}\sum_{u\in D_s}\tau_{u,s}\big(1-{\textrm{e}}^{-Z_s^u g(x)}\big) & = \int_0^s\mathbb{E}\big(Z_r-{\textbf{1}}_{\{o\in\mathcal{L}_r\}}\big)\mathbb{E}\big(1-{\textrm{e}}^{-Z_{s-r}g(x)}\big)\,{\rm d}r \\ & = \int_0^s\big({\textrm{e}}^{\lambda r}-{\textrm{e}}^{-\beta r}\big)\mathbb{E}\big(1-{\textrm{e}}^{-Z_{s-r} g(x)}\big)\,{\rm d}r, \end{align*}
which implies that
and
The final inequality follows from the fact that Supp
![]() $(g) \subset \{x \,:\,|x|> \delta\}$
. Since
$(g) \subset \{x \,:\,|x|> \delta\}$
. Since
![]() $v_\alpha({\textbf{1}}_{\{|x|>\delta\}})<\infty$
, using the dominated convergence theorem we get
$v_\alpha({\textbf{1}}_{\{|x|>\delta\}})<\infty$
, using the dominated convergence theorem we get
 $$ \lim_{s\to\infty}{\textrm{e}}^{-\lambda s}\int_{\mathbb{R}_0} \mathbb{E}\Bigg[\sum_{u\in D_s}\tau_{u,s}\big(1-{\textrm{e}}^{-Z_s^u g(x)}\big)\Bigg]\,v_\alpha({\rm d}x) = \int_0^\infty{\textrm{e}}^{-\lambda r}\int_{\mathbb{R}_0}\mathbb{E}\big(1-{\textrm{e}}^{-Z_{r} g(x)}\big)\,v_\alpha({\rm d}x)\,{\rm d}r, $$
$$ \lim_{s\to\infty}{\textrm{e}}^{-\lambda s}\int_{\mathbb{R}_0} \mathbb{E}\Bigg[\sum_{u\in D_s}\tau_{u,s}\big(1-{\textrm{e}}^{-Z_s^u g(x)}\big)\Bigg]\,v_\alpha({\rm d}x) = \int_0^\infty{\textrm{e}}^{-\lambda r}\int_{\mathbb{R}_0}\mathbb{E}\big(1-{\textrm{e}}^{-Z_{r} g(x)}\big)\,v_\alpha({\rm d}x)\,{\rm d}r, $$
which implies that
By Lemmas 2.6 and 2.4,
![]() $\lim_{t\to\infty}\mathbb{E}\Big({\textrm{e}}^{-\widetilde{\mathcal{N}}_{t}(g)}\Big) = E\big({\textrm{e}}^{-\mathcal{N}_\infty(g)}\big)$
. The proof is now complete.
$\lim_{t\to\infty}\mathbb{E}\Big({\textrm{e}}^{-\widetilde{\mathcal{N}}_{t}(g)}\Big) = E\big({\textrm{e}}^{-\mathcal{N}_\infty(g)}\big)$
. The proof is now complete.
3. Joint convergence of the order statistics
Proof of Corollary 1.1. Since
![]() $q_1>0$
, we have, for all
$q_1>0$
, we have, for all
![]() $k\ge 1$
,
$k\ge 1$
,
![]() $M_{(k)}>0$
,
$M_{(k)}>0$
,
![]() $P^*$
-a.s.
$P^*$
-a.s.
Note that, for any
![]() $x\in\overline{\mathbb{R}}_0$
,
$x\in\overline{\mathbb{R}}_0$
,
![]() $\mathcal{N}_{\infty}(\{x\})=0,$
a.s. Since
$\mathcal{N}_{\infty}(\{x\})=0,$
a.s. Since
![]() $\{M_{t,k}\le h_t x\}=\{\mathcal{N}_t(x,\infty)\le k-1\}$
for any
$\{M_{t,k}\le h_t x\}=\{\mathcal{N}_t(x,\infty)\le k-1\}$
for any
![]() $x>0$
, by Remark 1.1 with
$x>0$
, by Remark 1.1 with
![]() $B_k=(x_k,\infty)$
, we have, for any
$B_k=(x_k,\infty)$
, we have, for any
![]() $n\ge 1$
and
$n\ge 1$
and
![]() $x_1,x_2,x_3,\ldots,x_{n}>0$
,
$x_1,x_2,x_3,\ldots,x_{n}>0$
,
 \begin{align*} \mathbb{P}(M_{t,1}\le h_t x_1, & M_{t,2}\le h_t x_2, M_{t,3}\le h_t x_3,\ldots, M_{t,n}\le h_t x_{n}) \\[3pt] & = \mathbb{P}(\mathcal{N}_{t}(x_k,\infty)\le k-1, k=1,\ldots,n) \\[3pt] & \to P(\mathcal{N}_{\infty}(x_k,\infty)\le k-1,k=1,\ldots,n) \\[3pt] & = P\big(M_{(1)}\le x_1 ,M_{(2)}\le x_2, M_{(3)}\le x_3,\ldots, M_{(n)}\le x_{n}\big) \quad \text{as } t\to\infty. \end{align*}
\begin{align*} \mathbb{P}(M_{t,1}\le h_t x_1, & M_{t,2}\le h_t x_2, M_{t,3}\le h_t x_3,\ldots, M_{t,n}\le h_t x_{n}) \\[3pt] & = \mathbb{P}(\mathcal{N}_{t}(x_k,\infty)\le k-1, k=1,\ldots,n) \\[3pt] & \to P(\mathcal{N}_{\infty}(x_k,\infty)\le k-1,k=1,\ldots,n) \\[3pt] & = P\big(M_{(1)}\le x_1 ,M_{(2)}\le x_2, M_{(3)}\le x_3,\ldots, M_{(n)}\le x_{n}\big) \quad \text{as } t\to\infty. \end{align*}
Thus, as
![]() $t\to\infty$
,
$t\to\infty$
,
 \begin{align} \mathbb{P}^*\big(M_{t,1}\le h_t & x_1, M_{t,2}\le h_t x_2,\ldots, M_{t,n}\le h_t x_{n}\big) \nonumber \\[3pt] & = \mathbb{P}(\mathcal{S})^{-1}\big[\mathbb{P}\big(M_{t,k}\le h_t x_k,k=1,\ldots,n\big) - \mathbb{P}\big(M_{t,k}\le h_t x_k,k=1,\ldots,n, \mathcal{S}^\textrm{c}\big)\big] \nonumber \\[3pt] & \to \mathbb{P}(\mathcal{S})^{-1}\big[P\big(M_{(k)}\le x_k,k=1,\ldots,n\big)-\mathbb{P}\big(\mathcal{S}^\textrm{c}\big)\big]\nonumber\\[3pt] & = P^*\big(M_{(k)}\le x_k,k=1,\ldots,n\big), \end{align}
\begin{align} \mathbb{P}^*\big(M_{t,1}\le h_t & x_1, M_{t,2}\le h_t x_2,\ldots, M_{t,n}\le h_t x_{n}\big) \nonumber \\[3pt] & = \mathbb{P}(\mathcal{S})^{-1}\big[\mathbb{P}\big(M_{t,k}\le h_t x_k,k=1,\ldots,n\big) - \mathbb{P}\big(M_{t,k}\le h_t x_k,k=1,\ldots,n, \mathcal{S}^\textrm{c}\big)\big] \nonumber \\[3pt] & \to \mathbb{P}(\mathcal{S})^{-1}\big[P\big(M_{(k)}\le x_k,k=1,\ldots,n\big)-\mathbb{P}\big(\mathcal{S}^\textrm{c}\big)\big]\nonumber\\[3pt] & = P^*\big(M_{(k)}\le x_k,k=1,\ldots,n\big), \end{align}
where in the final equality we used the fact that on the event of extinction,
![]() $M_{(k)}=-\infty$
,
$M_{(k)}=-\infty$
,
![]() $k\ge 1$
.
$k\ge 1$
.
Now we consider the case
![]() $x_1,\ldots,x_n\in \mathbb{R}$
with
$x_1,\ldots,x_n\in \mathbb{R}$
with
![]() $x_i\le 0$
for some i and
$x_i\le 0$
for some i and
![]() $x_j>0$
,
$x_j>0$
,
![]() $j\neq i$
. By (3.1), for any
$j\neq i$
. By (3.1), for any
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
 \begin{multline*} \limsup_{t\to\infty}\mathbb{P}^*\big(M_{t,1}\le h_t x_1 ,M_{t,2}\le h_t x_2,\ldots, M_{t,n}\le h_t x_{n}\big) \\ \le \lim_{t\to\infty}\mathbb{P}^*\big(M_{t,j}\le h_t x_j, j\neq i, M_{t,i}\le h_t \varepsilon\big) = P^*\big(M_{(j)}\le x_j,j\neq i, M_{(i)}\le \varepsilon\big). \end{multline*}
\begin{multline*} \limsup_{t\to\infty}\mathbb{P}^*\big(M_{t,1}\le h_t x_1 ,M_{t,2}\le h_t x_2,\ldots, M_{t,n}\le h_t x_{n}\big) \\ \le \lim_{t\to\infty}\mathbb{P}^*\big(M_{t,j}\le h_t x_j, j\neq i, M_{t,i}\le h_t \varepsilon\big) = P^*\big(M_{(j)}\le x_j,j\neq i, M_{(i)}\le \varepsilon\big). \end{multline*}
The right-hand side of the display above tends to 0 as
![]() $\varepsilon\to0$
since
$\varepsilon\to0$
since
![]() $M_{(i)}>0$
a.s. Thus,
$M_{(i)}>0$
a.s. Thus,
Similarly, this can be shown to hold for any
![]() $x_1,\ldots,x_n\in \mathbb{R}$
.
$x_1,\ldots,x_n\in \mathbb{R}$
.
The proof is now complete.
4. Examples and an extension
This section provides more examples satisfying (H2) and an extension.
Lemma 4.1.
Assume that
![]() $L^*$
is a positive function on
$L^*$
is a positive function on
![]() $(0,\infty)$
slowly varying at
$(0,\infty)$
slowly varying at
![]() $\infty$
such that
$\infty$
such that
![]() $l_\varepsilon(x)\,:\!=\,\sup_{y\in(0,x]}y^{\varepsilon}L^*(y)<\infty$
for any
$l_\varepsilon(x)\,:\!=\,\sup_{y\in(0,x]}y^{\varepsilon}L^*(y)<\infty$
for any
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $x>0$
. Then, for any
$x>0$
. Then, for any
![]() $\varepsilon>0$
, there exist
$\varepsilon>0$
, there exist
![]() $c_\varepsilon, C_\varepsilon>0$
such that, for any
$c_\varepsilon, C_\varepsilon>0$
such that, for any
![]() $y>0$
and
$y>0$
and
![]() $a>c_\varepsilon$
,
$a>c_\varepsilon$
,
Proof. By [Reference Bingham, Goldie and Teugels11, Theorem 1.5.6], for any
![]() $\varepsilon>0$
there exists
$\varepsilon>0$
there exists
![]() $c_\varepsilon>0$
such that, for any
$c_\varepsilon>0$
such that, for any
![]() $a \ge c_\varepsilon$
and
$a \ge c_\varepsilon$
and
![]() $y \ge a^{-1}c_\varepsilon$
,
$y \ge a^{-1}c_\varepsilon$
,
Thus, for any
![]() $a>c_\varepsilon$
,
$a>c_\varepsilon$
,
Hence, for
![]() $a>c_\varepsilon$
and
$a>c_\varepsilon$
and
![]() $0<y\le a^{-1}c_\varepsilon$
,
$0<y\le a^{-1}c_\varepsilon$
,
Combining (4.1) and (4.2), there exists
![]() $C_\varepsilon>0$
such that, for any
$C_\varepsilon>0$
such that, for any
![]() $y>0$
and
$y>0$
and
![]() $a>c_\varepsilon$
,
$a>c_\varepsilon$
,
Example 4.1. Let
![]() $n({\rm d}y) = c_1x^{-(1+\alpha)}L^*(x){\textbf{1}}_{(0,\infty)}(x){\rm d}x + c_2|x|^{-(1+\alpha)}L^*(|x|){\textbf{1}}_{({-}\infty,0)}(x){\rm d}x$
, where
$n({\rm d}y) = c_1x^{-(1+\alpha)}L^*(x){\textbf{1}}_{(0,\infty)}(x){\rm d}x + c_2|x|^{-(1+\alpha)}L^*(|x|){\textbf{1}}_{({-}\infty,0)}(x){\rm d}x$
, where
![]() $\alpha\in(0,2)$
,
$\alpha\in(0,2)$
,
![]() $c_1,c_2\ge0$
,
$c_1,c_2\ge0$
,
![]() $c_1+c_2>0$
, and
$c_1+c_2>0$
, and
![]() $L^*$
is a positive function on
$L^*$
is a positive function on
![]() $(0, \infty)$
slowly varying at
$(0, \infty)$
slowly varying at
![]() $\infty$
such that
$\infty$
such that
![]() $\sup_{y\in(0,x]}y^{\varepsilon}L^*(y)<\infty$
for any
$\sup_{y\in(0,x]}y^{\varepsilon}L^*(y)<\infty$
for any
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $x>0$
.
$x>0$
.
-
(i) For
 $\alpha\in(0,1)$
, assume that the Lévy exponent of
$\alpha\in(0,1)$
, assume that the Lévy exponent of
 $\xi$
has the form where
$\xi$
has the form where $$\psi(\theta)={\textrm{i}} a\theta - b^2\theta^2 + \int\big({\textrm{e}}^{{\textrm{i}} \theta y}-1\big)\,n({\rm d}y),$$
$$\psi(\theta)={\textrm{i}} a\theta - b^2\theta^2 + \int\big({\textrm{e}}^{{\textrm{i}} \theta y}-1\big)\,n({\rm d}y),$$
 $a\in\mathbb{R}$
,
$a\in\mathbb{R}$
,
 $b\ge0$
. Using Lemma 4.1 with
$b\ge0$
. Using Lemma 4.1 with
 $\varepsilon\in (0, (1-\alpha)\wedge \alpha)$
we have, by the dominated convergence theorem, as
$\varepsilon\in (0, (1-\alpha)\wedge \alpha)$
we have, by the dominated convergence theorem, as
 $\theta\to 0_+$
, Thus as
$\theta\to 0_+$
, Thus as \begin{align*} \int _0^\infty\big({\textrm{e}}^{{\textrm{i}} \theta y}-1\big)\,n({\rm d}y) & = \theta^\alpha\int_0^\infty\big({\textrm{e}}^{{\textrm{i}} y}-1\big)y^{-1-\alpha}L^*\big(\theta^{-1}y\big)\,{\rm d}y \\ & \sim \theta^\alpha L^*\big(\theta^{-1}\big)\int_0^\infty\big({\textrm{e}}^{{\textrm{i}} y}-1\big)y^{-1-\alpha}\,{\rm d}y = -\alpha\Gamma(1-\alpha){\textrm{e}}^{-{\textrm{i}} \pi\alpha/2}\theta^\alpha L^*\big(\theta^{-1}\big), \\ \int_{-\infty}^0\big({\textrm{e}}^{{\textrm{i}} \theta y}-1\big)\,n({\rm d}y) & = \theta^\alpha \int _0^\infty \big({\textrm{e}}^{-{\textrm{i}} y}-1\big)y^{-1-\alpha}L^*\big(\theta^{-1}y\big)\,{\rm d}y \\ & \sim \theta^\alpha L^*\big(\theta^{-1}\big)\int_0^\infty \big({\textrm{e}}^{-{\textrm{i}} y}-1\big)y^{-1-\alpha}\,{\rm d}y = -\alpha\Gamma(1-\alpha){\textrm{e}}^{{\textrm{i}} \pi\alpha/2}\theta^\alpha L^*\big(\theta^{-1}\big). \end{align*}
\begin{align*} \int _0^\infty\big({\textrm{e}}^{{\textrm{i}} \theta y}-1\big)\,n({\rm d}y) & = \theta^\alpha\int_0^\infty\big({\textrm{e}}^{{\textrm{i}} y}-1\big)y^{-1-\alpha}L^*\big(\theta^{-1}y\big)\,{\rm d}y \\ & \sim \theta^\alpha L^*\big(\theta^{-1}\big)\int_0^\infty\big({\textrm{e}}^{{\textrm{i}} y}-1\big)y^{-1-\alpha}\,{\rm d}y = -\alpha\Gamma(1-\alpha){\textrm{e}}^{-{\textrm{i}} \pi\alpha/2}\theta^\alpha L^*\big(\theta^{-1}\big), \\ \int_{-\infty}^0\big({\textrm{e}}^{{\textrm{i}} \theta y}-1\big)\,n({\rm d}y) & = \theta^\alpha \int _0^\infty \big({\textrm{e}}^{-{\textrm{i}} y}-1\big)y^{-1-\alpha}L^*\big(\theta^{-1}y\big)\,{\rm d}y \\ & \sim \theta^\alpha L^*\big(\theta^{-1}\big)\int_0^\infty \big({\textrm{e}}^{-{\textrm{i}} y}-1\big)y^{-1-\alpha}\,{\rm d}y = -\alpha\Gamma(1-\alpha){\textrm{e}}^{{\textrm{i}} \pi\alpha/2}\theta^\alpha L^*\big(\theta^{-1}\big). \end{align*}
 $\theta\to 0_+$
,
$\theta\to 0_+$
,
 $\psi(\theta)\sim-\alpha\Gamma(1-\alpha)\big({\textrm{e}}^{-{\textrm{i}} \pi\alpha/2}c_1+{\textrm{e}}^{{\textrm{i}} \pi\alpha/2}c_2\big)\theta^\alpha L^*\big(\theta^{-1}\big)$
.
$\psi(\theta)\sim-\alpha\Gamma(1-\alpha)\big({\textrm{e}}^{-{\textrm{i}} \pi\alpha/2}c_1+{\textrm{e}}^{{\textrm{i}} \pi\alpha/2}c_2\big)\theta^\alpha L^*\big(\theta^{-1}\big)$
.
-
(ii) For
 $\alpha\in(1,2)$
, assume that the Lévy exponent of
$\alpha\in(1,2)$
, assume that the Lévy exponent of
 $\xi$
has the form where
$\xi$
has the form where $$\psi(\theta)=-b^2\theta^2+\int \big({\textrm{e}}^{{\textrm{i}} \theta y}-1-{\textrm{i}} \theta y\big)\,n({\rm d}y),$$
$$\psi(\theta)=-b^2\theta^2+\int \big({\textrm{e}}^{{\textrm{i}} \theta y}-1-{\textrm{i}} \theta y\big)\,n({\rm d}y),$$
 $b\ge0$
. Using Lemma 4.1 with
$b\ge0$
. Using Lemma 4.1 with
 $\varepsilon\in (0, (2-\alpha)\wedge(\alpha-1))$
, we have, by the dominated convergence theorem, as
$\varepsilon\in (0, (2-\alpha)\wedge(\alpha-1))$
, we have, by the dominated convergence theorem, as
 $\theta\to 0_+$
, Thus, as
$\theta\to 0_+$
, Thus, as \begin{align*} \int _0^\infty\big({\textrm{e}}^{{\textrm{i}} \theta y}-1-{\textrm{i}} \theta y\big)\,n({\rm d}y) & = \theta^\alpha \int_0^\infty\big(e^{{\textrm{i}} y}-1-{\textrm{i}} y\big)y^{-1-\alpha}L^*\big(\theta^{-1}y\big)\,{\rm d}y \\ & \sim \theta^\alpha L^*\big(\theta^{-1}\big)\int_0^\infty({\textrm{e}}^{{\textrm{i}} y}-1+{\textrm{i}} y)y^{-1-\alpha}\,{\rm d}y \\ & = -\alpha\Gamma(1-\alpha){\textrm{e}}^{-{\textrm{i}} \pi\alpha/2}\theta^\alpha L^*\big(\theta^{-1}\big), \\ \int _{-\infty}^0 \big({\textrm{e}}^{{\textrm{i}} \theta y}-1-{\textrm{i}} \theta y\big)\,n({\rm d}y) & = \theta^\alpha \int_0^\infty ({\textrm{e}}^{-{\textrm{i}} y}-1+{\textrm{i}} y)y^{-1-\alpha}L^*\big(\theta^{-1}y\big)\,{\rm d}y \\ & \sim \theta^\alpha L^*\big(\theta^{-1}\big)\int _0^\infty \big({\textrm{e}}^{-{\textrm{i}} y}-1+{\textrm{i}} y\big)y^{-1-\alpha}\,{\rm d}y \\ & = -\alpha\Gamma(1-\alpha){\textrm{e}}^{{\textrm{i}} \pi\alpha/2}\theta^\alpha L^*\big(\theta^{-1}\big). \end{align*}
\begin{align*} \int _0^\infty\big({\textrm{e}}^{{\textrm{i}} \theta y}-1-{\textrm{i}} \theta y\big)\,n({\rm d}y) & = \theta^\alpha \int_0^\infty\big(e^{{\textrm{i}} y}-1-{\textrm{i}} y\big)y^{-1-\alpha}L^*\big(\theta^{-1}y\big)\,{\rm d}y \\ & \sim \theta^\alpha L^*\big(\theta^{-1}\big)\int_0^\infty({\textrm{e}}^{{\textrm{i}} y}-1+{\textrm{i}} y)y^{-1-\alpha}\,{\rm d}y \\ & = -\alpha\Gamma(1-\alpha){\textrm{e}}^{-{\textrm{i}} \pi\alpha/2}\theta^\alpha L^*\big(\theta^{-1}\big), \\ \int _{-\infty}^0 \big({\textrm{e}}^{{\textrm{i}} \theta y}-1-{\textrm{i}} \theta y\big)\,n({\rm d}y) & = \theta^\alpha \int_0^\infty ({\textrm{e}}^{-{\textrm{i}} y}-1+{\textrm{i}} y)y^{-1-\alpha}L^*\big(\theta^{-1}y\big)\,{\rm d}y \\ & \sim \theta^\alpha L^*\big(\theta^{-1}\big)\int _0^\infty \big({\textrm{e}}^{-{\textrm{i}} y}-1+{\textrm{i}} y\big)y^{-1-\alpha}\,{\rm d}y \\ & = -\alpha\Gamma(1-\alpha){\textrm{e}}^{{\textrm{i}} \pi\alpha/2}\theta^\alpha L^*\big(\theta^{-1}\big). \end{align*}
 $\theta\to 0_+$
,
$\theta\to 0_+$
,
 $\psi(\theta)\sim-\alpha\Gamma(1-\alpha)\big({\textrm{e}}^{-{\textrm{i}} \pi\alpha/2}c_1+{\textrm{e}}^{{\textrm{i}} \pi\alpha/2}c_2\big)\theta^\alpha L^*\big(\theta^{-1}\big).$
$\psi(\theta)\sim-\alpha\Gamma(1-\alpha)\big({\textrm{e}}^{-{\textrm{i}} \pi\alpha/2}c_1+{\textrm{e}}^{{\textrm{i}} \pi\alpha/2}c_2\big)\theta^\alpha L^*\big(\theta^{-1}\big).$
-
(iii) For
 $\alpha=1$
, assume that
$\alpha=1$
, assume that
 $c_1=c_2$
and the Lévy exponent of
$c_1=c_2$
and the Lévy exponent of
 $\xi$
has the form where
$\xi$
has the form where $$\psi(\theta)={\textrm{i}} a\theta-b^2\theta^2+\int\big({\textrm{e}}^{{\textrm{i}} \theta y}-1-{\textrm{i}} \theta y{\textbf{1}}_{|y|\le 1}\big)\,n({\rm d}y),$$
$$\psi(\theta)={\textrm{i}} a\theta-b^2\theta^2+\int\big({\textrm{e}}^{{\textrm{i}} \theta y}-1-{\textrm{i}} \theta y{\textbf{1}}_{|y|\le 1}\big)\,n({\rm d}y),$$
 $a\in\mathbb{R}$
,
$a\in\mathbb{R}$
,
 $b\ge0$
. Since
$b\ge0$
. Since
 $c_1=c_2$
, we have Using Lemma 4.1 with
$c_1=c_2$
, we have Using Lemma 4.1 with \begin{equation*} \int_{-\infty}^\infty\big({\textrm{e}}^{{\textrm{i}} \theta y}-1-{\textrm{i}} \theta y{\textbf{1}}_{|y|\le 1}\big)\,n({\rm d}y) = -2c_1\theta \int_0^\infty (1-\cos y)y^{-2}L^*\big(\theta^{-1}y\big)\,{\rm d}y. \end{equation*}
\begin{equation*} \int_{-\infty}^\infty\big({\textrm{e}}^{{\textrm{i}} \theta y}-1-{\textrm{i}} \theta y{\textbf{1}}_{|y|\le 1}\big)\,n({\rm d}y) = -2c_1\theta \int_0^\infty (1-\cos y)y^{-2}L^*\big(\theta^{-1}y\big)\,{\rm d}y. \end{equation*}
 $\varepsilon\in (0, 1)$
, we have, by the dominated convergence theorem, which implies that as
$\varepsilon\in (0, 1)$
, we have, by the dominated convergence theorem, which implies that as $$\lim_{\theta\to 0_+}L^*\big(\theta^{-1}\big)^{-1}\int _0^\infty(1-\cos y)y^{-2}L^*\big(\theta^{-1}y\big)\,{\rm d}y = \int_0^\infty(1-\cos y)y^{-2}\,{\rm d}y = \pi/2,$$
$$\lim_{\theta\to 0_+}L^*\big(\theta^{-1}\big)^{-1}\int _0^\infty(1-\cos y)y^{-2}L^*\big(\theta^{-1}y\big)\,{\rm d}y = \int_0^\infty(1-\cos y)y^{-2}\,{\rm d}y = \pi/2,$$
 $\theta\to 0_+$
,
$\theta\to 0_+$
,
 $\psi(\theta)\sim-(c_1\pi-{\textrm{i}} a)\theta L^*\big(\theta^{-1}\big)$
.
$\psi(\theta)\sim-(c_1\pi-{\textrm{i}} a)\theta L^*\big(\theta^{-1}\big)$
.
Remark 4.1. (An extension.) Checking the proof of Theorem 1.1, we see that Theorem 1.1 holds for more general branching Lévy processes with spatial motions satisfying the following assumptions:
-
(A1) There exist a non-increasing function
 $h_t$
with
$h_t$
with
 $h_t\uparrow \infty$
and a measure
$h_t\uparrow \infty$
and a measure
 $\pi({\rm d}x)\in \mathcal{M}\big(\overline{\mathbb{R}}_0\big)$
such that
$\pi({\rm d}x)\in \mathcal{M}\big(\overline{\mathbb{R}}_0\big)$
such that  $$ \lim_{t\to\infty}{\textrm{e}}^{\lambda t}{\rm E}\big(g\big(h_t^{-1}\xi_s\big)\big) = s\int_{\mathbb{R}_0}g(x)\,\pi({\rm d}x), \qquad g\in C_\textrm{c}^+\big(\overline{\mathbb{R}}_0\big). $$
$$ \lim_{t\to\infty}{\textrm{e}}^{\lambda t}{\rm E}\big(g\big(h_t^{-1}\xi_s\big)\big) = s\int_{\mathbb{R}_0}g(x)\,\pi({\rm d}x), \qquad g\in C_\textrm{c}^+\big(\overline{\mathbb{R}}_0\big). $$
-
(A2)
 ${\textrm{e}}^{\lambda t}p_t^2\to0$
, where
${\textrm{e}}^{\lambda t}p_t^2\to0$
, where
 $p_t\,:\!=\,\sup_{s\le t}{\rm P}(|\xi_s|>h_t\theta/t)$
.
$p_t\,:\!=\,\sup_{s\le t}{\rm P}(|\xi_s|>h_t\theta/t)$
. -
(A3) For any
 $\theta>0$
,
$\theta>0$
,
 $\sup_{t>1}\sup_{s\le t}s^{-1}{\textrm{e}}^{\lambda t}{\rm P}(|\xi_s|>h_t\theta)<\infty$
.
$\sup_{t>1}\sup_{s\le t}s^{-1}{\textrm{e}}^{\lambda t}{\rm P}(|\xi_s|>h_t\theta)<\infty$
.
First, (H2) implies (A1)–(A3). Next, we explain that Theorem 1.1 holds under assumptions (A1)–(A3). Checking the proof of Lemma 2.5, we see that Lemma 2.5 holds under conditions (A1)–(A3). In fact, we may replace Lemma 2.2 by (A2) to get (2.3) (see (2.5) and (2.6)). For the proof of Lemma 2.6, using (A3) we get that
![]() $\mathbb{P} \big(J_{s,t}^\textrm{c}\big)\le C{\textrm{e}}^{-\lambda t}\mathbb{E}\sum_{u:b_u\le t-s}\tau_{u,t}$
, which says that (2.10) holds. Thus, (2.9) holds using the same arguments as in Lemma 2.6. Replacing Lemma 2.1 by (A1), we see that Proposition 2.1 holds with
$\mathbb{P} \big(J_{s,t}^\textrm{c}\big)\le C{\textrm{e}}^{-\lambda t}\mathbb{E}\sum_{u:b_u\le t-s}\tau_{u,t}$
, which says that (2.10) holds. Thus, (2.9) holds using the same arguments as in Lemma 2.6. Replacing Lemma 2.1 by (A1), we see that Proposition 2.1 holds with
![]() $v_\alpha$
replaced by
$v_\alpha$
replaced by
![]() $\pi({\rm d}x)$
. So, under (A1)–(A3), Theorem 1.1 holds with
$\pi({\rm d}x)$
. So, under (A1)–(A3), Theorem 1.1 holds with
![]() $v_\alpha$
replaced by
$v_\alpha$
replaced by
![]() $\pi({\rm d}x)$
.
$\pi({\rm d}x)$
.
An easy example which satisfies (A1)–(A3) but not (H2) is the non-symmetric 1-stable process. Assume
![]() $\xi$
is a non-symmetric 1-stable process with Lévy measure
$\xi$
is a non-symmetric 1-stable process with Lévy measure
![]() $n({\textrm{d}} x) = c_1x^{-2}{\textbf{1}}_{(0,\infty)}(x)\,{\rm d}x + c_2|x|^{-2}{\textbf{1}}_{({-}\infty,0)}(x)\,{\rm d}x$
, where
$n({\textrm{d}} x) = c_1x^{-2}{\textbf{1}}_{(0,\infty)}(x)\,{\rm d}x + c_2|x|^{-2}{\textbf{1}}_{({-}\infty,0)}(x)\,{\rm d}x$
, where
![]() $c_1,c_2\ge 0$
,
$c_1,c_2\ge 0$
,
![]() $c_1+c_2>0$
, and
$c_1+c_2>0$
, and
![]() $c_1\neq c_2$
. The Lévy exponent of
$c_1\neq c_2$
. The Lévy exponent of
![]() $\xi$
is given, for
$\xi$
is given, for
![]() $\theta>0$
, by
$\theta>0$
, by
where a is constant. Thus,
![]() $c_*={\textrm{i}} (c_1-c_2)$
. So
$c_*={\textrm{i}} (c_1-c_2)$
. So
![]() $\psi(\theta)$
does not satisfy (H2) since
$\psi(\theta)$
does not satisfy (H2) since
![]() ${\textrm{Re}}(c_*)=0$
.
${\textrm{Re}}(c_*)=0$
.
By [Reference Bertoin7, Section 1.5, Exercise 1],
![]() $({1}/{t}){\rm P}(\xi_t\in \cdot)\overset{\textrm{v}}{\to}n({\rm d} x)$
as
$({1}/{t}){\rm P}(\xi_t\in \cdot)\overset{\textrm{v}}{\to}n({\rm d} x)$
as
![]() $t\to 0$
. Since
$t\to 0$
. Since
![]() ${\textrm{e}}^{-\lambda t}\xi_s\overset{\textrm{d}}{=}\xi_{s{\textrm{e}}^{-\lambda t}}+(c_1-c_2)s\lambda t{\textrm{e}}^{-\lambda t}$
for
${\textrm{e}}^{-\lambda t}\xi_s\overset{\textrm{d}}{=}\xi_{s{\textrm{e}}^{-\lambda t}}+(c_1-c_2)s\lambda t{\textrm{e}}^{-\lambda t}$
for
![]() $s,t>0$
, we have
$s,t>0$
, we have
![]() ${\textrm{e}}^{\lambda t}{\rm P}({\textrm{e}}^{-\lambda t}\xi_s\in \cdot)\overset{\textrm{v}}{\to}s\,n({\rm d}x)$
as
${\textrm{e}}^{\lambda t}{\rm P}({\textrm{e}}^{-\lambda t}\xi_s\in \cdot)\overset{\textrm{v}}{\to}s\,n({\rm d}x)$
as
![]() $t\to\infty$
. So (A1) holds with
$t\to\infty$
. So (A1) holds with
![]() $h_t={\textrm{e}}^{\lambda t}$
. We claim that, for any
$h_t={\textrm{e}}^{\lambda t}$
. We claim that, for any
![]() $x>0$
and
$x>0$
and
![]() $s>0$
,
$s>0$
,
where c is a constant. Thus it is easy to prove that (A2) and (A3) hold.
In fact, for any
![]() $x>0$
,
$x>0$
,
Note that
 \begin{align*} 1-{\textrm{Re}}\big({\textrm{e}}^{s\psi(\theta)}\big) & = 1-{\textrm{e}}^{s{\textrm{Re}}(\psi(\theta))}\cos[s{\textrm{Im}}(\psi(\theta))] \\ & = 1-{\textrm{e}}^{s{\textrm{Re}}(\psi(\theta))}+{\textrm{e}}^{s{\textrm{Re}}(\psi(\theta))}(1-\cos[s{\textrm{Im}}(\psi(\theta))]) \\ & \le -s{\textrm{Re}}(\psi(\theta))+s^2[{\textrm{Im}}(\psi(\theta))]^2 \\ & = \frac{\pi}{2}(c_1+c_2)s\theta + (c_1-c_2)^2s^2(a-\log\theta)^2\theta^2. \end{align*}
\begin{align*} 1-{\textrm{Re}}\big({\textrm{e}}^{s\psi(\theta)}\big) & = 1-{\textrm{e}}^{s{\textrm{Re}}(\psi(\theta))}\cos[s{\textrm{Im}}(\psi(\theta))] \\ & = 1-{\textrm{e}}^{s{\textrm{Re}}(\psi(\theta))}+{\textrm{e}}^{s{\textrm{Re}}(\psi(\theta))}(1-\cos[s{\textrm{Im}}(\psi(\theta))]) \\ & \le -s{\textrm{Re}}(\psi(\theta))+s^2[{\textrm{Im}}(\psi(\theta))]^2 \\ & = \frac{\pi}{2}(c_1+c_2)s\theta + (c_1-c_2)^2s^2(a-\log\theta)^2\theta^2. \end{align*}
Thus, we have
 \begin{align*} {\rm P}(|\xi_s|>x) & \le \pi(c_1+c_2)sx^{-1}+(c_1-c_2)^2s^2x^{-2}\int_0^2(a-\log\theta+\log x)^2\theta^2\,{\rm d}\theta \\ & \le \pi(c_1+c_2)sx^{-1}+2(c_1-c_2)^2s^2x^{-2}\int_0^2[(a-\log\theta)^2+(\log x)^2]\theta^2\,{\rm d}\theta \\ & \le c\big(sx^{-1}+s^2x^{-2}+s^2x^{-2}(\log x)^2\big), \end{align*}
\begin{align*} {\rm P}(|\xi_s|>x) & \le \pi(c_1+c_2)sx^{-1}+(c_1-c_2)^2s^2x^{-2}\int_0^2(a-\log\theta+\log x)^2\theta^2\,{\rm d}\theta \\ & \le \pi(c_1+c_2)sx^{-1}+2(c_1-c_2)^2s^2x^{-2}\int_0^2[(a-\log\theta)^2+(\log x)^2]\theta^2\,{\rm d}\theta \\ & \le c\big(sx^{-1}+s^2x^{-2}+s^2x^{-2}(\log x)^2\big), \end{align*}
which proves the claim (4.3).
5. Frontal position of Fisher–KPP equation
The Fisher-KPP equation related to our branching Lévy process is given by
where
![]() $\mathcal{A}$
is the generator of the Lévy process
$\mathcal{A}$
is the generator of the Lévy process
![]() $\{(\xi_t)_{t\ge0}, {\rm P}\}$
,
$\{(\xi_t)_{t\ge0}, {\rm P}\}$
,
![]() $\varphi(s)=\beta\big(\sum_k s^kp_k-s\big)$
,
$\varphi(s)=\beta\big(\sum_k s^kp_k-s\big)$
,
![]() $u_0(x)\in[0,1]$
,
$u_0(x)\in[0,1]$
,
![]() $x\in\mathbb{R}$
; see, for instance, [Reference Cabré and Roquejoffre17].
$x\in\mathbb{R}$
; see, for instance, [Reference Cabré and Roquejoffre17].
Recall that, for any
![]() $g\in C_\textrm{b}^+(\mathbb{R})$
,
$g\in C_\textrm{b}^+(\mathbb{R})$
,
![]() $u_g(t,x)=\mathbb{E}\big(\exp\big\{{-}\sum_{v\in\mathcal{L}_t}g\big(\xi^v_t+x\big)\big\}\big)$
satisfies (1.5), and thus is a mild solution of the following Cauchy problem:
$u_g(t,x)=\mathbb{E}\big(\exp\big\{{-}\sum_{v\in\mathcal{L}_t}g\big(\xi^v_t+x\big)\big\}\big)$
satisfies (1.5), and thus is a mild solution of the following Cauchy problem:
Hence
![]() $1-u_g(t,x)$
is a mild solution to (5.1) with
$1-u_g(t,x)$
is a mild solution to (5.1) with
![]() $u_0(x)=1-{\textrm{e}}^{-g(x)}$
.
$u_0(x)=1-{\textrm{e}}^{-g(x)}$
.
We are interested in the large-time behavior of
![]() $1-u_g(t,x)$
. For
$1-u_g(t,x)$
. For
![]() $\theta \in (0,1)$
, the level set
$\theta \in (0,1)$
, the level set
![]() $\{x\in\mathbb{R}\,:\, 1-u_g(t,x)=\theta\}$
is also called the front of
$\{x\in\mathbb{R}\,:\, 1-u_g(t,x)=\theta\}$
is also called the front of
![]() $1-u_g$
. The evolution of the front of
$1-u_g$
. The evolution of the front of
![]() $1-u_g$
as time goes to
$1-u_g$
as time goes to
![]() $\infty$
is of considerable interest. Using analytic methods, it was shown in [Reference Aronson and Weinberger5] that, if
$\infty$
is of considerable interest. Using analytic methods, it was shown in [Reference Aronson and Weinberger5] that, if
![]() $\xi$
is a standard Brownian motion, the frontal position of branching Brownian motion is
$\xi$
is a standard Brownian motion, the frontal position of branching Brownian motion is
![]() $\sqrt{2\lambda}t$
, with
$\sqrt{2\lambda}t$
, with
![]() $\lambda$
given by (1.2). More precisely, under the condition that g is compactly supported, if
$\lambda$
given by (1.2). More precisely, under the condition that g is compactly supported, if
![]() $c>\sqrt{2\lambda}$
, then
$c>\sqrt{2\lambda}$
, then
![]() $1-u_g(t,x)\to 0$
uniformly in
$1-u_g(t,x)\to 0$
uniformly in
![]() $\{|x|\ge ct\}$
as
$\{|x|\ge ct\}$
as
![]() $t\to\infty$
; if
$t\to\infty$
; if
![]() $c<\sqrt{2\lambda}$
, then
$c<\sqrt{2\lambda}$
, then
![]() $1-u_g(t,x)\to 1$
uniformly in
$1-u_g(t,x)\to 1$
uniformly in
![]() $\{|x|\le ct\}$
as
$\{|x|\le ct\}$
as
![]() $t\to\infty$
. But if the density of
$t\to\infty$
. But if the density of
![]() $\xi$
is comparable to that of a symmetric
$\xi$
is comparable to that of a symmetric
![]() $\alpha$
-stable process, [Reference Cabré and Roquejoffre17, Theorem 1.5] proved that the frontal position is exponential in time; see Remark 5.1 for the precise meaning. In this paper we provide a probabilistic proof of [Reference Cabré and Roquejoffre17, Theorem 1.5] using Corollary 1.2, and also partially generalize it.
$\alpha$
-stable process, [Reference Cabré and Roquejoffre17, Theorem 1.5] proved that the frontal position is exponential in time; see Remark 5.1 for the precise meaning. In this paper we provide a probabilistic proof of [Reference Cabré and Roquejoffre17, Theorem 1.5] using Corollary 1.2, and also partially generalize it.
Proposition 5.1.
Assume that
![]() $q_1>0$
.
$q_1>0$
.
-
(i) Assume that
 $a_t$
satisfies
$a_t$
satisfies
 $a_t/h_t\to \infty$
as
$a_t/h_t\to \infty$
as
 $t\to\infty$
, and that g is a non-negative function satisfying (5.2)Then
$t\to\infty$
, and that g is a non-negative function satisfying (5.2)Then \begin{equation} {\textrm{e}}^{\lambda t}\sup_{x\le -a_t/2}g(x)\to 0 \quad \text{ as } t\to\infty. \end{equation}
\begin{equation} {\textrm{e}}^{\lambda t}\sup_{x\le -a_t/2}g(x)\to 0 \quad \text{ as } t\to\infty. \end{equation}
 $\lim_{t\to\infty}\sup_{x\le -a_t}(1-u_g(t,x))=0$
.
$\lim_{t\to\infty}\sup_{x\le -a_t}(1-u_g(t,x))=0$
.
-
(ii) Assume that
 $c_t$
satisfies
$c_t$
satisfies
 $c_t/h_t\to 0$
as
$c_t/h_t\to 0$
as
 $t\to\infty$
, and that g is a non-negative function satisfying
$t\to\infty$
, and that g is a non-negative function satisfying
 $a_0\,:\!=\,\liminf_{x\to\infty} g(x)>0$
. Then
$a_0\,:\!=\,\liminf_{x\to\infty} g(x)>0$
. Then  $$\lim_{t\to\infty}\sup_{x\ge -c_t}|u_g(t,x)-\mathbb{P} (\mathcal{S}^\textrm{c})|=0.$$
$$\lim_{t\to\infty}\sup_{x\ge -c_t}|u_g(t,x)-\mathbb{P} (\mathcal{S}^\textrm{c})|=0.$$
Proof. (i) Let
![]() $g^*(x)=\sup_{y\le-x}g(y)$
. Note that, for
$g^*(x)=\sup_{y\le-x}g(y)$
. Note that, for
![]() $x\leq -a_t$
,
$x\leq -a_t$
,
 \begin{align} 1-u_g(t,x) & = \mathbb{E}\Bigg(1-\exp\Bigg\{{-}\sum_{v\in\mathcal{L}_t}g\big(\xi^v_t+x\big)\Bigg\}\Bigg) \nonumber \\ & \le \mathbb{P}(R_t\ge a_t/2) + \mathbb{E}\Bigg(1-\exp\Bigg\{{-}\sum_{v\in\mathcal{L}_t}g\big(\xi^v_t+x\big)\Bigg\};R_t<a_t/2\Bigg) \nonumber \\ & \le \mathbb{P}(R_t\ge a_t/2) + \mathbb{E}\big(1-{\textrm{e}}^{-g^*(a_t/2)Z_t}\big) \nonumber \\ & \le \mathbb{P}(R_t\ge a_t/2) + {\textrm{e}}^{\lambda t}g^*(a_t/2), \end{align}
\begin{align} 1-u_g(t,x) & = \mathbb{E}\Bigg(1-\exp\Bigg\{{-}\sum_{v\in\mathcal{L}_t}g\big(\xi^v_t+x\big)\Bigg\}\Bigg) \nonumber \\ & \le \mathbb{P}(R_t\ge a_t/2) + \mathbb{E}\Bigg(1-\exp\Bigg\{{-}\sum_{v\in\mathcal{L}_t}g\big(\xi^v_t+x\big)\Bigg\};R_t<a_t/2\Bigg) \nonumber \\ & \le \mathbb{P}(R_t\ge a_t/2) + \mathbb{E}\big(1-{\textrm{e}}^{-g^*(a_t/2)Z_t}\big) \nonumber \\ & \le \mathbb{P}(R_t\ge a_t/2) + {\textrm{e}}^{\lambda t}g^*(a_t/2), \end{align}
where in the second inequality we used the fact that, on the event
![]() $\{R_t<a_t/2\}$
,
$\{R_t<a_t/2\}$
,
![]() $\xi^v_t+x<a_t/2-a_t=-a_t/2$
and
$\xi^v_t+x<a_t/2-a_t=-a_t/2$
and
![]() $g\big(\xi^v_t+x\big)\le g^*(a_t/2)$
. By the assumption (5.2),
$g\big(\xi^v_t+x\big)\le g^*(a_t/2)$
. By the assumption (5.2),
![]() ${\textrm{e}}^{\lambda t}g^*(a_t/2)\to 0$
. By Corollary 1.2,
${\textrm{e}}^{\lambda t}g^*(a_t/2)\to 0$
. By Corollary 1.2,
![]() $\mathbb{P} ^*(R_t\ge a_t/2)\to0$
. Thus
$\mathbb{P} ^*(R_t\ge a_t/2)\to0$
. Thus
as
![]() $t\to\infty$
. Thus, by (5.3),
$t\to\infty$
. Thus, by (5.3),
![]() $\lim_{t\to\infty}\sup_{x\le -a_t}(1-u_g(t,x))=0$
.
$\lim_{t\to\infty}\sup_{x\le -a_t}(1-u_g(t,x))=0$
.
(ii) Note that
 \begin{equation*} |u_g(t,x)-\mathbb{P}(\mathcal{S}^\textrm{c})| \le \mathbb{E}\Bigg(\exp\Bigg\{{-}\sum_{v\in\mathcal{L}_t}g\big(\xi^v_t+x\big)\Bigg\};\,\mathcal{S}\Bigg) + \mathbb{E}\Bigg(1-\exp\Bigg\{{-}\sum_{v\in\mathcal{L}_t}g\big(\xi^v_t+x\big)\Bigg\};\,\mathcal{S}^\textrm{c}\Bigg). \end{equation*}
\begin{equation*} |u_g(t,x)-\mathbb{P}(\mathcal{S}^\textrm{c})| \le \mathbb{E}\Bigg(\exp\Bigg\{{-}\sum_{v\in\mathcal{L}_t}g\big(\xi^v_t+x\big)\Bigg\};\,\mathcal{S}\Bigg) + \mathbb{E}\Bigg(1-\exp\Bigg\{{-}\sum_{v\in\mathcal{L}_t}g\big(\xi^v_t+x\big)\Bigg\};\,\mathcal{S}^\textrm{c}\Bigg). \end{equation*}
Noticing that on the event
![]() $Z_t=0$
,
$Z_t=0$
,
![]() $1-\exp\big\{{-}\sum_{v\in\mathcal{L}_t}g\big(\xi^v_t+x\big)\big\}=0$
, we get, for any
$1-\exp\big\{{-}\sum_{v\in\mathcal{L}_t}g\big(\xi^v_t+x\big)\big\}=0$
, we get, for any
![]() $x\in\mathbb{R}$
,
$x\in\mathbb{R}$
,
![]() $\mathbb{E}\big(1-\exp\big\{{-}\sum_{v\in\mathcal{L}_t}g\big(\xi^v_t+x\big)\big\};\,\mathcal{S}^\textrm{c}\big) \le \mathbb{P}(Z_t>0;\, \mathcal{S}^\textrm{c})\to 0$
as
$\mathbb{E}\big(1-\exp\big\{{-}\sum_{v\in\mathcal{L}_t}g\big(\xi^v_t+x\big)\big\};\,\mathcal{S}^\textrm{c}\big) \le \mathbb{P}(Z_t>0;\, \mathcal{S}^\textrm{c})\to 0$
as
![]() $t\to\infty$
. Let
$t\to\infty$
. Let
![]() $g_*(x)=\inf_{y\ge x}g(y)$
. Since
$g_*(x)=\inf_{y\ge x}g(y)$
. Since
![]() $c_t/h_t\to 0$
for any
$c_t/h_t\to 0$
for any
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $t_\varepsilon>0$
such that
$t_\varepsilon>0$
such that
![]() $c_t\le \varepsilon h_t$
for
$c_t\le \varepsilon h_t$
for
![]() $t>t_\varepsilon$
. For any
$t>t_\varepsilon$
. For any
![]() $t>t_\varepsilon$
and
$t>t_\varepsilon$
and
![]() $x\geq-c_t$
,
$x\geq-c_t$
,
 \begin{align*} \mathbb{E}\Bigg(\exp\Bigg\{{-}\sum_{v\in\mathcal{L}_t}g\big(\xi^v_t+x\big)\Bigg\};\,\mathcal{S}\Bigg) & \le \mathbb{E}\Bigg(\exp\Bigg\{{-}g_*(c_t)\sum_{v\in\mathcal{L}_t}{\textbf{1}}_{\xi^v_t>2c_t}\Bigg\};\, \mathcal{S}\Bigg) \\ & \le \mathbb{E}\Bigg(\exp\Bigg\{{-}g_*(c_t)\sum_{v\in\mathcal{L}_t}{\textbf{1}}_{\xi^v_t>2\varepsilon h_t}\Bigg\};\, \mathcal{S}\Bigg) \\ & = \mathbb{E}\big({\textrm{e}}^{-g_*(c_t)\mathcal{N}_t(2\varepsilon,\infty)};\,\mathcal{S}\big). \end{align*}
\begin{align*} \mathbb{E}\Bigg(\exp\Bigg\{{-}\sum_{v\in\mathcal{L}_t}g\big(\xi^v_t+x\big)\Bigg\};\,\mathcal{S}\Bigg) & \le \mathbb{E}\Bigg(\exp\Bigg\{{-}g_*(c_t)\sum_{v\in\mathcal{L}_t}{\textbf{1}}_{\xi^v_t>2c_t}\Bigg\};\, \mathcal{S}\Bigg) \\ & \le \mathbb{E}\Bigg(\exp\Bigg\{{-}g_*(c_t)\sum_{v\in\mathcal{L}_t}{\textbf{1}}_{\xi^v_t>2\varepsilon h_t}\Bigg\};\, \mathcal{S}\Bigg) \\ & = \mathbb{E}\big({\textrm{e}}^{-g_*(c_t)\mathcal{N}_t(2\varepsilon,\infty)};\,\mathcal{S}\big). \end{align*}
Thus
Since on the event
![]() $\mathcal{S}$
,
$\mathcal{S}$
,
![]() $\vartheta W v_\alpha(0,\infty)=\infty$
, we have
$\vartheta W v_\alpha(0,\infty)=\infty$
, we have
![]() $\mathcal{N}_\infty(0,\infty)=\infty$
. Now letting
$\mathcal{N}_\infty(0,\infty)=\infty$
. Now letting
![]() $\varepsilon\to 0$
in (5.4) we get the desired result.
$\varepsilon\to 0$
in (5.4) we get the desired result.
Remark 5.1. Proposition 5.1 is a slight generalization of [Reference Cabré and Roquejoffre17, Theorem 1.5]. Assume that
![]() $p_0=0$
, which ensures that
$p_0=0$
, which ensures that
![]() $\mathbb{P}(\mathcal{S}^\textrm{c})=0$
. If
$\mathbb{P}(\mathcal{S}^\textrm{c})=0$
. If
![]() $L=1$
, then
$L=1$
, then
![]() $h_t={\textrm{e}}^{\lambda t/\alpha}$
, and we have the following results:
$h_t={\textrm{e}}^{\lambda t/\alpha}$
, and we have the following results:
-
(i) Let g be a non-negative measurable function satisfying
(5.5)Then, for any \begin{equation} g(x)\le C|x|^{-\alpha},\qquad x<0. \end{equation}
\begin{equation} g(x)\le C|x|^{-\alpha},\qquad x<0. \end{equation}
 $\gamma>\lambda/\alpha$
,
$\gamma>\lambda/\alpha$
,
 ${\textrm{e}}^{\lambda t}g^*({-}{\textrm{e}}^{\gamma t}/2)\le C2^{\alpha}{\textrm{e}}^{\lambda t}{\textrm{e}}^{-\alpha\gamma t}\to 0$
. Thus, by Proposition 5.1,
${\textrm{e}}^{\lambda t}g^*({-}{\textrm{e}}^{\gamma t}/2)\le C2^{\alpha}{\textrm{e}}^{\lambda t}{\textrm{e}}^{-\alpha\gamma t}\to 0$
. Thus, by Proposition 5.1,
 $\lim_{t\to\infty}\sup_{x\le -{\textrm{e}}^{\gamma t}}(1-u_g(t,x))=0$
.
$\lim_{t\to\infty}\sup_{x\le -{\textrm{e}}^{\gamma t}}(1-u_g(t,x))=0$
.
-
(ii) Assume that g is a non-negative function satisfying
 $a_0\,:\!=\,\liminf_{x\to\infty} g(x)>0$
. For any
$a_0\,:\!=\,\liminf_{x\to\infty} g(x)>0$
. For any
 $\gamma<\lambda/\alpha$
, by Proposition 5.1 we have
$\gamma<\lambda/\alpha$
, by Proposition 5.1 we have
 $\lim_{t\to\infty}\sup_{x\ge -{\textrm{e}}^{\gamma t}}u_g(t,x)=0$
.
$\lim_{t\to\infty}\sup_{x\ge -{\textrm{e}}^{\gamma t}}u_g(t,x)=0$
.
Note that in the notation of [Reference Cabré and Roquejoffre17],
![]() $\sigma^{**}=\lambda/\alpha$
, and our condition (5.5) is equivalent to
$\sigma^{**}=\lambda/\alpha$
, and our condition (5.5) is equivalent to
![]() $1-{\textrm{e}}^{-g(x)} \le C|x|^{-\alpha}$
,
$1-{\textrm{e}}^{-g(x)} \le C|x|^{-\alpha}$
,
![]() $x<0$
, for some constant C. If g is non-decreasing, it is clear that
$x<0$
, for some constant C. If g is non-decreasing, it is clear that
![]() $\liminf_{x\to\infty}g(x)>0$
. Thus, when the Lévy process
$\liminf_{x\to\infty}g(x)>0$
. Thus, when the Lévy process
![]() $\xi$
satisfies (H2) with
$\xi$
satisfies (H2) with
![]() $L=1$
, we can get that the conclusion of [Reference Cabré and Roquejoffre17, Theorem 1.5] holds from Proposition 5.1. Note that the independent sum of Brownian motion and a symmetric
$L=1$
, we can get that the conclusion of [Reference Cabré and Roquejoffre17, Theorem 1.5] holds from Proposition 5.1. Note that the independent sum of Brownian motion and a symmetric
![]() $\alpha$
-stable process satisfies (H2) with
$\alpha$
-stable process satisfies (H2) with
![]() $L=1$
, but its transition density is not comparable with that of the symmetric
$L=1$
, but its transition density is not comparable with that of the symmetric
![]() $\alpha$
-stable process, see [Reference Chen and Kumagai22, Reference Song and Vondraček39]. Note also that the independent sum of a symmetric
$\alpha$
-stable process, see [Reference Chen and Kumagai22, Reference Song and Vondraček39]. Note also that the independent sum of a symmetric
![]() $\alpha$
-stable process and a symmetric
$\alpha$
-stable process and a symmetric
![]() $\beta$
-stable process,
$\beta$
-stable process,
![]() $0<\alpha<\beta<2$
, also satisfies (H2) with
$0<\alpha<\beta<2$
, also satisfies (H2) with
![]() $L=1$
, but its transition density is not comparable with that of the symmetric
$L=1$
, but its transition density is not comparable with that of the symmetric
![]() $\alpha$
-stable process, see [Reference Chen and Kumagai21]. Note that in this paper we do not need to assume that g is non-decreasing. Thus Proposition 5.1 partially generalizes [Reference Cabré and Roquejoffre17, Theorem 1.5].
$\alpha$
-stable process, see [Reference Chen and Kumagai21]. Note that in this paper we do not need to assume that g is non-decreasing. Thus Proposition 5.1 partially generalizes [Reference Cabré and Roquejoffre17, Theorem 1.5].
Acknowledgements
We thank the referee for very helpful comments and suggestions.
Funding information
The research of Y.-X. Ren is supported by the National Key R&D Program of China (No. 2020YFA0712900) and NSFC (Grant Nos. 12071011 and 11731009). The research of R. Song is supported by a grant from the Simons Foundation (#960480, Renming Song). Part of the research for this paper was done while R. Song was visiting Jiangsu Normal University, where he was partially supported by a grant from the National Natural Science Foundation of China (11931004, Yingchao Xie). The research of R. Zhang is supported by NSFC (Grant Nos. 11601354, 12271374, and 12371143), Beijing Municipal Natural Science Foundation (Grant No. 1202004), and the Academy for Multidisciplinary Studies, Capital Normal University.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.