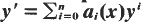This is the second of two papers in which we study the singularities of solutions of second-order linear elliptic boundary value problems at the edges of piecewise analytic domains in ℝ3. When the opening angle at the edge is variable, there appears trie phenomenon of “crossing” of the exponents of singularities. In Part I, we introduced for the Dirichlet problem appropriate combinations of the simple tensor product singularities.
In this second part, we extend the results of Part I to general non-homogeneous boundary conditions. Moreover, we show how these combinations of singularities appear in a natural way as sections of an analytic vector bundle above the edge. In the case when the interior operator is the Laplacian, we give a simpler expression of the combined singular functions, involving divided differences of powers of a complex variable describing the coordinates in the normal plane to the edge.