No CrossRef data available.
Article contents
Asymptotic behaviour of finite energy solutions of polyharmonic equations
Published online by Cambridge University Press: 14 November 2011
Synopsis
Asymptotic behaviour of solutions of polyharmonic equations
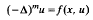
on exterior domains in Rn is considered under suitable conditions on f. It is shown that finite energysolutions u have the asymptotic property
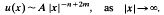
This partially extends results of Egnell [6] for m = 1.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 123 , Issue 2 , 1993 , pp. 345 - 354
- Copyright
- Copyright © Royal Society of Edinburgh 1993
References
1Agmon, S.. The Lp approach to the Dirichlet problem. Ann. Scuola Norm. Sup. Pisa 13 (1959), 405–448.Google Scholar
2Allegretto, W. and Yu, L. S.. Decaying solution of 2mth order elliptic problems. Canad. J. Math. 43 (1991), 449–460.CrossRefGoogle Scholar
3Aronszajn, N., Creese, T. M. and Lipkin, L. J.. Polyharmonic Functions (Oxford: Clarendon Press, 1983).Google Scholar
4Dalmasso, R.. Solutions positives globales d'une équation biharmonique sur-linéearie. C.R. Acad. Sci. Paris Ser. 1 Meth 308 (1989), 411–414.Google Scholar
5Edelson, A. L. and Vakilian, R.. Asymptotic behavior of higher order semilinear equations. Nonlinear Anal. 15 (1990), 17–26.Google Scholar
6Egnell, H.. Asymptotic results for finite energy solutions of semilinear elliptic equations (preprint).Google Scholar
7Gilbarg, D. and Trudinger, N. S.. Elliptic Partial Differential Equations of Second Order, 2nd edn (Berlin: Springer, 1983).Google Scholar
8Kusano, T., Naito, M. and Swanson, C. A.. Radial entire solutions of even order semilinear elliptic equations. Canad. J. Math 40 (1988), 1281–1300.CrossRefGoogle Scholar
9Noussair, E. S., Swanson, C. A. and , Yang Jianfu. Transcritical biharmonic equations in Rn. Funkcial Ekvac: (to appear).Google Scholar
11Yu, L. S.. Positive Decaying Solutions of Nonlinear Elliptic Problmes (Ph.D. Thesis, University of Alberta, 1990).Google Scholar


