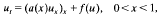Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rynne, Bryan P.
1996.
Genericity of hyperbolicity and saddle-node bifurcations in reaction-diffusion equations depending on a parameter.
ZAMP Zeitschrift f�r angewandte Mathematik und Physik,
Vol. 47,
Issue. 5,
p.
730.
Pereira, Antonio L.
2004.
Generic hyperbolicity for the equilibria of the one-dimensional parabolic equation ut=(a(x)ux)x+f(u).
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 56,
Issue. 4,
p.
485.
Pereira, Marcone C.
2007.
Generic simplicity of the eigenvalues for a supported plate equation.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 67,
Issue. 3,
p.
889.
Broche, Rita de Cássia D.S.
and
Pereira, Marcone C.
2010.
Generic hyperbolicity of stationary solutions for a reaction–diffusion system.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 72,
Issue. 12,
p.
4638.