In this paper, by the moving spheres method, Caffarelli-Silvestre extension formula and blow-up analysis, we study the local behaviour of nonnegative solutions to fractional elliptic equations
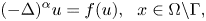 \begin{align*} (-\Delta)^{\alpha} u =f(u),~~ x\in \Omega\backslash \Gamma, \end{align*}
\begin{align*} (-\Delta)^{\alpha} u =f(u),~~ x\in \Omega\backslash \Gamma, \end{align*}
where
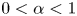 0<\alpha <1
0<\alpha <1,
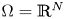 \Omega = \mathbb {R}^{N}
\Omega = \mathbb {R}^{N} or
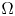 \Omega
\Omega is a smooth bounded domain,
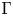 \Gamma
\Gamma is a singular subset of
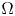 \Omega
\Omega with fractional capacity zero,
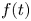 f(t)
f(t) is locally bounded and positive for
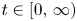 t\in [0,\,\infty )
t\in [0,\,\infty ), and
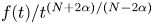 f(t)/t^{({N+2\alpha })/({N-2\alpha })}
f(t)/t^{({N+2\alpha })/({N-2\alpha })} is nonincreasing in
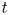 t
t for large
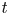 t
t, rather than for every
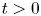 t>0
t>0. Our main result is that the solutions satisfy the estimate
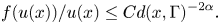 \begin{align*} f(u(x))/ u(x)\leq C d(x,\Gamma)^{{-}2\alpha}. \end{align*}
\begin{align*} f(u(x))/ u(x)\leq C d(x,\Gamma)^{{-}2\alpha}. \end{align*}
This estimate is new even for
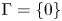 \Gamma =\{0\}
\Gamma =\{0\}. As applications, we derive the spherical Harnack inequality, asymptotic symmetry, cylindrical symmetry of the solutions.