Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T17:30:34.858Z Has data issue: false hasContentIssue false
  • English
  • Français

Discs area-minimizing in mean convex Riemannian n-manifolds

Part of: Global differential geometry

Published online by Cambridge University Press:  06 September 2021

Ezequiel Barbosa Open the ORCID record for Ezequiel Barbosa [Opens in a new window]  and
Franciele Conrado
Ezequiel Barbosa
Affiliation:
Universidade Federal de Minas Gerais (UFMG), Caixa Postal 702, 30123-970 Belo Horizonte, MG, Brazil ([email protected])
Franciele Conrado
Affiliation:
Instituto de Ciências Exatas, Universidade Federal de Minas Gerais, 30161-970 Belo Horizonte, MG, Brazil ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this work, we consider oriented compact manifolds which possess convex mean curvature boundary, positive scalar curvature and admit a map to 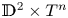$\mathbb {D}^{2}\times T^{n}$ with non-zero degree, where 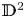$\mathbb {D}^{2}$ is a disc and 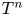$T^{n}$ is an 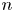$n$-dimensional torus. We prove the validity of an inequality involving a mean of the area and the length of the boundary of immersed discs whose boundaries are homotopically non-trivial curves. We also prove a rigidity result for the equality case when the boundary is strongly totally geodesic. This can be viewed as a partial generalization of a result due to Lucas Ambrózio in (2015, J. Geom. Anal., 25, 1001–1017) to higher dimensions.

Keywords

Free-boundarymanifolds with boundaryminimal surfacesrigidity resultsuniversal covering

MSC classification

Primary: 53C24: Rigidity results
Secondary: 53C42: Immersions (minimal, prescribed curvature, tight, etc.)
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 6 , December 2022 , pp. 1361 - 1382
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ambrozio, L. C.. Rigidity of area-minimizing free boundary surfaces in mean convex three-manifolds. J. Geom. Anal. 25 (2015), 1001–1017.CrossRefGoogle Scholar
Bray, H., Brendle, S., Eichmair, M. and Neves, A.. Area-minimizing projective planes in 3-manifolds. Commun. Pure Appl. Math. 63 (2010), 1237–1247.Google Scholar
Bray, H., Brendle, S. and Neves, A.. Rigidity of area-minimizing two-spheres in three-manifolds. Commun. Anal. Geom. 18 (2010), 822.CrossRefGoogle Scholar
Cai, M. and Galloway, G.. Rigidity of area minimizing tori in 3-manifolds of nonnegative scalar curvature. Commun. Anal. Geom. 8 (2000), 565–573.CrossRefGoogle Scholar
Chen, J., Fraser, A. and Pang, C.. Minimal immersions of compact bordered Riemann surfaces with free boundary. Trans. Am. Math. Soc. 367 (2012), 2487–2507.CrossRefGoogle Scholar
Folha, A., Pacard, F. and Zolotareva, T.. Free boundary minimal surfaces in the unit 3-ball. Manuscr. Math. 154 (2015), 359–409.CrossRefGoogle Scholar
Fraser, A.. Index estimates for minimal surfaces and $k$-convexity. Proc. Am. Math. Soc. 135 (2007), 3733–3744.CrossRefGoogle Scholar
Fraser, A. and Chun Li, M. M.. Compactness of the space of embedded minimal surfaces with free boundary in three-manifolds with nonnegative Ricci curvature and convex boundary. J. Differ. Geom. 96 (2014), 183–200.CrossRefGoogle Scholar
Fraser, A. and Sargent, P.. Existence and classification of $\mathbb {S}^{1}$-invariant free boundary minimal annuli and möbius bands in $\mathbb {B}n$. J. Geom. Anal. 31 (2021), 2703–2725.CrossRefGoogle Scholar
Fraser, A. and Schoen, R.. The first Steklov eigenvalue, conformal geometry, and minimal surfaces. Adv. Math. 226 (2009), 4011–4030.CrossRefGoogle Scholar
Fraser, A. and Schoen, R.. Minimal surfaces and eigenvalue problems. Geom. Anal. Math. Relativ. Nonlinear Partial Differ. Equ. 599 (2012), 105–121.CrossRefGoogle Scholar
Fraser, A. and Schoen, R.. Sharp eigenvalue bounds and minimal surfaces in the ball. Invent. Math. 203 (2012), 823–890.CrossRefGoogle Scholar
Fraser, A. and Schoen, R.. Shape optimization for the Steklov problem in higher dimensions. Adv. Math. 348 (2019), 146–162.CrossRefGoogle Scholar
Li, M.. Free boundary minimal surfaces in the unit ball: Recent advances and open questions. ArXiv preprint arXiv:1907.05053, 2019.Google Scholar
Li, H. and Xiong, C.. Stability of capillary hypersurfaces in a manifold with density. Int. J. Math. 27 (2016), 1650062.CrossRefGoogle Scholar
Mazet, L. and Rosenberg, H.. On minimal spheres of area 4$\pi$ and rigidity. Comment. Math. Helv. 89 (2012), 921–928.CrossRefGoogle Scholar
Miao, P.. Positive mass theorem on manifolds admitting corners along a hypersurface. Adv. Theor. Math. Phys. 6 (2002), 1163–1182.CrossRefGoogle Scholar
Micallef, M. and Moraru, V.. Splitting of 3-manifolds and rigidity of area-minimising surfaces. Proc. Am. Math. Soc. 143 (2011), 2868.Google Scholar
Nunes, I.. Rigidity of area-minimizing hyperbolic surfaces in three-manifolds. J. Geom. Anal. 23 (2013), 1290–1302.CrossRefGoogle Scholar
Simon, L.. Lectures on geometric measure theory. Vol. 3 (The Australian National University, Mathematical Sciences Institute, Centre for Mathematics and its Applications, 1983). Proc. Centre Math. Appl. 3 (1984), 272.Google Scholar
Zhu, J.. Rigidity of area-minimizing 2-spheres in n-manifolds with positive scalar curvature. Proc. Am. Math. Soc. 148 (2020), 3479–3489.CrossRefGoogle Scholar