Article contents
Global regularity for the micropolar Rayleigh-Bénard problem with only velocity dissipation
Published online by Cambridge University Press: 26 August 2021
Abstract
This paper is concerned with the global regularity problem on the micropolar Rayleigh-Bénard problem with only velocity dissipation in 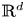 $\mathbb {R}^{d}$ with
$\mathbb {R}^{d}$ with 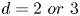 $d=2\ or\ 3$. By fully exploiting the special structure of the system, introducing two combined quantities and using the technique of Littlewood-Paley decomposition, we establish the global regularity of solutions to this system in
$d=2\ or\ 3$. By fully exploiting the special structure of the system, introducing two combined quantities and using the technique of Littlewood-Paley decomposition, we establish the global regularity of solutions to this system in 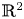 $\mathbb {R}^{2}$. Moreover, we obtain the global regularity for fractional hyperviscosity case in
$\mathbb {R}^{2}$. Moreover, we obtain the global regularity for fractional hyperviscosity case in 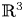 $\mathbb {R}^{3}$ by employing various techniques including energy methods, the regularization of generalized heat operators on the Fourier frequency localized functions and logarithmic Sobolev interpolation inequalities.
$\mathbb {R}^{3}$ by employing various techniques including energy methods, the regularization of generalized heat operators on the Fourier frequency localized functions and logarithmic Sobolev interpolation inequalities.
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 5 , October 2022 , pp. 1109 - 1138
- Copyright
- Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh
References
- 6
- Cited by



