Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T17:49:44.538Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalized small cancellation conditions, non-positive curvature and diagrammatic reducibility

Part of: Semigroups Algebraic structures Special aspects of infinite or finite groups

Published online by Cambridge University Press:  02 March 2021

Martín Axel Blufstein ,
Elías Gabriel Minian  and
Iván Sadofschi Costa
Martín Axel Blufstein
Affiliation:
Departamento de Matemática - IMAS FCEyN, Universidad de Buenos Aires, Buenos Aires, Argentina ([email protected]; [email protected]; [email protected])
Elías Gabriel Minian
Affiliation:
Departamento de Matemática - IMAS FCEyN, Universidad de Buenos Aires, Buenos Aires, Argentina ([email protected]; [email protected]; [email protected])
Iván Sadofschi Costa
Affiliation:
Departamento de Matemática - IMAS FCEyN, Universidad de Buenos Aires, Buenos Aires, Argentina ([email protected]; [email protected]; [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a metric condition 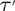$\TTMetric$ which describes the geometry of classical small cancellation groups and applies also to other known classes of groups such as two-dimensional Artin groups. We prove that presentations satisfying condition 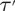$\TTMetric$ are diagrammatically reducible in the sense of Sieradski and Gersten. In particular, we deduce that the standard presentation of an Artin group is aspherical if and only if it is diagrammatically reducible. We show that, under some extra hypotheses, 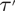$\TTMetric$-groups have quadratic Dehn functions and solvable conjugacy problem. In the spirit of Greendlinger's lemma, we prove that if a presentation P = 〈X| R〉 of group G satisfies conditions 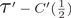$\TTMetric -C'(\frac {1}{2})$, the length of any nontrivial word in the free group generated by X representing the trivial element in G is at least that of the shortest relator. We also introduce a strict metric condition 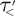$\TTMetricStrict$, which implies hyperbolicity.

Keywords

Small cancellation theoryword problemDehn functionArtin groupsnon-positive curvatureconjugacy problemhyperbolic groupsisoperimetric inequality

MSC classification

Primary: 20F65: Geometric group theory
Secondary: 20F67: Hyperbolic groups and nonpositively curved groups 20F06: Cancellation theory; application of van Kampen diagrams 20F10: Word problems, other decision problems, connections with logic and automata 08A50: Word problems 20M05: Free semigroups, generators and relations, word problems
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 3 , June 2022 , pp. 545 - 566
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ballmann, W. and Buyalo, S.. Nonpositively curved metrics on 2-polyhedra. Math. Z. 222 (1996), 97–134.CrossRefGoogle Scholar
Barmak, J. A. and Minian, E. G.. A new test for asphericity and diagrammatic reducibility of group presentations. Proc. R. Soc. Edin. Sect. A 150 (2020), 871–895.CrossRefGoogle Scholar
Baumslag, G., Miller, C. F. III and Short, H.. Isoperimetric inequalities and the homology of groups. Invent. Math. 113 (1993), 531–560.CrossRefGoogle Scholar
Blufstein, M. A. and Minian, E. G.. Strictly systolic angled complexes and hyperbolicity of one-relator groups. Preprint, https://arxiv.org/abs/1907.06738, 2019.Google Scholar
Bridson, M. R. and Haefliger, A.. Metric spaces of non-positive curvature, volume 319 of Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences] (Berlin: Springer-Verlag, 1999).CrossRefGoogle Scholar
Charney, R. and Davis, M. W.. The K(π, 1)-problem for hyperplane complements associated to infinite reflection groups. J. Am. Math. Soc. 8 (1995), 597–627.Google Scholar
Charney, R. and Davis, M. W.. Finite K(π, 1)s for Artin groups. In Frank Quinn (ed.), Prospects in topology (Princeton, NJ, 1994), volume 138 of Ann. Math. Stud., pp. 110–124 (Princeton, NJ: Princeton Univ. Press, 1995).Google Scholar
Chermak, A.. Locally non-spherical Artin groups. J. Algebra 200 (1998), 56–98.CrossRefGoogle Scholar
Dehn, M.. Über unendliche diskontinuierliche Gruppen. Math. Ann. 71 (1911), 116–144.CrossRefGoogle Scholar
Dehn, M.. Transformation der Kurven auf zweiseitigen Flächen. Math. Ann. 72 (1912), 413–421.CrossRefGoogle Scholar
Edjvet, M.. On irreducible cyclic presentations. J. Group Theory 6 (2003), 261–270.CrossRefGoogle Scholar
Epstein, D. B. A., Cannon, J. W., Holt, D. F., Levy, S. V. F., Paterson, M. S. and Thurston, W. P.. Word processing in groups (Boston, MA: Jones and Bartlett Publishers, 1992).CrossRefGoogle Scholar
Gersten, S. M.. Reducible diagrams and equations over groups. In S. M. Gersten (ed.), Essays in group theory, volume 8 of Math. Sci. Res. Inst. Publ., pp. 15–73 (New York: Springer, 1987).CrossRefGoogle Scholar
Gersten, S. M.. Branched coverings of 2-complexes and diagrammatic reducibility. Trans. Am. Math. Soc. 303 (1987), 689–706.CrossRefGoogle Scholar
Greendlinger, M.. Dehn's algorithm for the word problem. Commun. Pure Appl. Math. 13 (1960), 67–83.CrossRefGoogle Scholar
Greendlinger, M.. On Dehn's algorithms for the conjugacy and word problems, with applications. Commun. Pure Appl. Math. 13 (1960), 641–677.CrossRefGoogle Scholar
Gromov, M.. Hyperbolic groups. In S. M. Gersten (ed.), Essays in group theory, volume 8 of Math. Sci. Res. Inst. Publ., pp. 75–263 (New York: Springer, 1987).CrossRefGoogle Scholar
Gromov, M.. Random walk in random groups. Geom. Funct. Anal. 13 (2003), 73–146.CrossRefGoogle Scholar
Gruber, D.. Groups with graphical C(6) and C(7) small cancellation presentations. Trans. Am. Math. Soc. 367 (2015), 2051–2078.CrossRefGoogle Scholar
Huang, J. and Osajda, D.. Metric systolicity and two-dimensional Artin groups. Math. Ann 374 (2019), 1311–1352.CrossRefGoogle Scholar
Klyachko, A. and Thom, A.. New topological methods to solve equations over groups. Algebr. Geom. Topol. 17 (2017), 331–353.CrossRefGoogle Scholar
Lyndon, R. C.. On Dehn's algorithm. Math. Ann. 166 (1966), 208–228.CrossRefGoogle Scholar
Lyndon, R. C. and Schupp, P. E.. Classics in Mathematics. Combinatorial group theory (Berlin: Springer-Verlag, 2001). Reprint of the 1977 edition.CrossRefGoogle Scholar
Ollivier, Y.. On a small cancellation theorem of Gromov. Bull. Belg. Math. Soc. Simon Stevin 13 (2006), 75–89.CrossRefGoogle Scholar
Olshanskiĭ, A. Y.. Geometry of defining relations in groups, volume 70 of Mathematics and its Applications (Soviet Series) (Dordrecht: Kluwer Academic Publishers Group, 1991). Translated from the 1989 Russian original by Yu. A. Bakhturin.CrossRefGoogle Scholar
Rips, E.. Generalized small cancellation theory and applications. I. The word problem. Israel J. Math. 41 (1982), 1–146.CrossRefGoogle Scholar
Rips, E.. Another characterization of finitely generated groups with a solvable word problem. Bull. London Math. Soc. 14 (1982), 43–44.CrossRefGoogle Scholar
Rips, E.. Subgroups of small cancellation groups. Bull. London Math. Soc. 14 (1982), 45–47.CrossRefGoogle Scholar
Sadofschi Costa, I.. SmallCancellation – Metric and nonmetric small cancellation conditions, Version 1.0.4. GAP package, https://doi.org/10.5281/zenodo.3906472 DOI: 10.5281/zenodo.3906472, 2020.CrossRefGoogle Scholar
Schiek, H.. Ähnlichkeitsanalyse von Gruppenrelationen. Acta Math. 96 (1956), 157–252.CrossRefGoogle Scholar
Schupp, P. E.. On Dehn's algorithm and the conjugacy problem. Math. Ann. 178 (1968), 119–130.CrossRefGoogle Scholar
Sieradski, A. J.. A coloring test for asphericity. Quart. J. Math. Oxford Ser. (2) 34 (1983), 97–106.CrossRefGoogle Scholar
Steenbock, M.. Rips-Segev torsion-free groups without the unique product property. J. Algebra 438 (2015), 337–378.CrossRefGoogle Scholar
Tartakovskiĭ, V. A.. Solution of the word problem for groups with a k-reduced basis for k > 6. Izvestiya Akad. Nauk SSSR. Ser. Mat. 13 (1949), 483–494.Google Scholar
The GAP Group. GAP – Groups, Algorithms, and Programming, Version 4.10.1, 2019.CrossRefGoogle Scholar
Wang, X., Li, G., Yang, L. and Lin, H.. Groups with two generators having unsolvable word problem and presentations of Mihailova subgroups of braid groups. Commun. Algebra 44 (2016), 3020–3037.CrossRefGoogle Scholar
Wise, D. T.. Nonpositive immersions, sectional curvature, and subgroup properties. Electron. Res. Announc. Am. Math. Soc. 9 (2003), 1–9.CrossRefGoogle Scholar
Wise, D. T.. Sectional curvature, compact cores, and local quasiconvexity. Geom. Funct. Anal. 14 (2004), 433–468.CrossRefGoogle Scholar