Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T17:05:13.478Z Has data issue: false hasContentIssue false
  • English
  • Français

Recollements, comma categories and morphic enhancements

Part of: Abelian categories General theory of categories and functors

Published online by Cambridge University Press:  09 March 2021

Xiao-Wu Chen  and
Jue Le
Xiao-Wu Chen
Affiliation:
Key Laboratory of Wu Wen-Tsun Mathematics, Chinese Academy of Sciences, School of Mathematical Sciences, University of Science and Technology of China, Hefei 230026, Anhui, PR China ([email protected], [email protected])
Jue Le
Affiliation:
Key Laboratory of Wu Wen-Tsun Mathematics, Chinese Academy of Sciences, School of Mathematical Sciences, University of Science and Technology of China, Hefei 230026, Anhui, PR China ([email protected], [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

For each recollement of triangulated categories, there is an epivalence between the middle category and the comma category associated with a triangle functor from the category on the right to the category on the left. For a morphic enhancement of a triangulated category 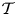$\mathcal {T}$, there are three explicit ideals of the enhancing category, whose corresponding factor categories are all equivalent to the module category over 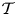$\mathcal {T}$. Examples related to inflation categories and weighted projective lines are discussed.

Keywords

Recollementcomma categorymorphic enhancementsubmodule categoryweighted projective line

MSC classification

Primary: 18E30: Derived categories, triangulated categories
Secondary: 18A25: Functor categories, comma categories 18E10: Exact categories, abelian categories
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 3 , June 2022 , pp. 567 - 591
Check for updates
Copyright
Copyright © The Author(s) 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Auslander, M. and Reiten, I.. On the representation type of triangular matrix rings. J. Lond. Math. Soc. (2) 12 (1976), 371–382.CrossRefGoogle Scholar
Auslander, M., Reiten, I. and Smalø, S.O.. Representation theory of artin algebras, Cambridge Studies in Adv. Math., vol. 36 (Cambridge: Cambridge University Press, 1995).CrossRefGoogle Scholar
Bondal, A. I. and Kapranov, M. M.. Representable functors, Serre functors, and reconstructions. Izv. Akad. Nauk SSSR Ser. Mat. 53 (1989), 1183–1205.Google Scholar
Beilinson, A. A., Bernstein, J. and Deligne, P.. Faisceaux pervers, Astérisque, vol. 100 (France, Paris: Soc. Math., 1982).Google Scholar
Chen, X. W.. The stable monomorphism category of a Frobenius category. Math. Res. Lett. 18 (2011), 125–137.CrossRefGoogle Scholar
Chen, X. W.. Three results on Frobenius categories. Math. Z. 270 (2012), 43–58.CrossRefGoogle Scholar
Franjou, V. and Pirashvili, T.. Comparison of abelian categories recollements. Doc. Math. 9 (2004), 41–56.Google Scholar
Eiriksson, Ö.. From submodule categories to the stable Auslander algebra. J. Algebra 486 (2017), 98–118.CrossRefGoogle Scholar
Fossum, R. M., Griffith, P. A. and Reiten, I.. Trivial Extensions of Abelian Categories, Lecture Notes in Math., vol. 456 (Berlin, Heidelberg: Springer-Verlag, 1975).CrossRefGoogle Scholar
Gabriel, P. and Roiter, A. V.. Representations of Finite-Dimensional Algebras, Encyclopaedia Math. Sciences, vol. 73 (Berlin, Heidelberg: Springer-Verlag, 1977).Google Scholar
Geigle, W., Lenzing, H., A class of weighted projective curves arising in representation theory of finite dimensional algebras, in: Singularities, representations of algebras and vector bundles, Lecture Notes in Math., vol. 1273, pp. 265–297 (Springer-Verlag Berlin Heidelberg, 1987).Google Scholar
Geiss, Ch.. Derived tame algebras and Euler-forms with an appendix by Ch. Geiss and B. Keller. Math. Z. 239 (2002), 829–862.Google Scholar
Iyama, O., Kato, K. and Miyachi, J. I.. Recollement of homotopy categories and Cohen–Macaulay modules, J. K-Theory 8 (2011), 507–542.CrossRefGoogle Scholar
Keller, B.. Chain complexes and stable categories. Manuscr. Math. 67 (1990), 379–417.CrossRefGoogle Scholar
Keller, B.. Derived categories and universal problems. Commun. Algebra 19 (1991), 699–747.Google Scholar
Krause, H.. Cohomological quotients and smashing localizations. Amer. J. Math. 127 (2005), 1197–1246.CrossRefGoogle Scholar
Krause, H.. Completing perfect complexes, with appendices by T. Barthel and B. Keller. Math. Z. 296 (2020), 1387–1427.CrossRefGoogle Scholar
Kussin, D., Lenzing, H. and Meltzer, H.. Triangle singularities, ADE-chains and weighted projective lines. Adv. Math. 237 (2013), 194–251.CrossRefGoogle Scholar
Kussin, D., Lenzing, H. and Meltzer, H.. Nilpotent operators and weighted projective lines. J. Reine Angew. Math. 685 (2013), 33–71.Google Scholar
Kuznetsov, A. and Lunts, V. A.. Categorical resolutions of irrational singularities. Inter. Math. Res. Not. IMRN 13 (2015), 4536–4625.CrossRefGoogle Scholar
Li, Z. W.. Zhang, P.. A construction of Gorenstein-projective modules. J. Algebra 323 (2010), 1802–1812.CrossRefGoogle Scholar
Lin, Z.. Abelian quotients of the categories of short exact sequences. J. Algebra 551 (2020), 61–92.CrossRefGoogle Scholar
Neeman, A.. Triangulated Categories, Ann. Math. Stud., vol. 148 (Princeton: Univ. Press, 2001).CrossRefGoogle Scholar
Ringel, C. M. and Schmidmeier, M.. The Auslander–Reiten translation in submodule category. Trans. Am. Math. Soc. 360 (2008), 691–716.CrossRefGoogle Scholar
Ringel, C. M. and Schmidmeier, M.. Invariant subspaces of nilpotent linear operators I. J. Reine Angew. Math. 614 (2008), 1–52.CrossRefGoogle Scholar
Ringel, C. M. and Zhang, P.. From submodule categories to preprojective algebras. Math. Z. 278 (2014), 55–73.CrossRefGoogle Scholar
Rouquier, R.. Dimensions of triangulated categories. J. K-Theory 1 (2008), 193–256.CrossRefGoogle Scholar