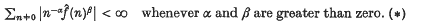Research Article
Läuchli's algebraic closure of Q
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 289-297
-
- Article
- Export citation
Structure of a foliated neighbourhood
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 101-110
-
- Article
- Export citation
Three notes on proximity theory
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 299-305
-
- Article
- Export citation
On the fractional parts of certain additive forms
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 463-467
-
- Article
- Export citation
On the axiomatics of nearness and compression
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 469-471
-
- Article
- Export citation
Strictly singular and cosingular operators
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 111-115
-
- Article
- Export citation
Hilbert space methods in the theory of Jordan algebras. II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 307-319
-
- Article
- Export citation
Gleason parts for measure algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 321-327
-
- Article
- Export citation
Borsuk shape and a generalization of Grothendieck's definition of pro-category
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 473-482
-
- Article
- Export citation
Integrability of singular distributions on Banach manifolds
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 117-128
-
- Article
- Export citation
On a class of Volterra and Fredholm non-linear integral equations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 329-335
-
- Article
- Export citation
On the Lusternik–Schnirelmann category of Grassmannians
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 129-134
-
- Article
- Export citation
Operations on K-theory of torsion-free spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 483-491
-
- Article
- Export citation
Derangements and Laguerre polynomials
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 135-143
-
- Article
- Export citation
The disintegration of invariant measures
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 337-341
-
- Article
- Export citation
Orthonormal systems in Banach spaces and their applications
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 493-510
-
- Article
- Export citation
A higher catastrophe machine
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 343-350
-
- Article
- Export citation
The wave front set of the solution of a simple initial-boundary value problem with glancing rays
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 145-159
-
- Article
- Export citation
Unbounded operators and random Fourier series
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 511-520
-
- Article
- Export citation
A class of approximate exterior rotating solutions of Einstein's equations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 161-166
-
- Article
- Export citation

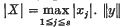 is the distance from the real number
is the distance from the real number 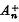 is the (finite-dimensional) Jordan algebra of all complex
is the (finite-dimensional) Jordan algebra of all complex 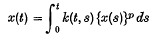
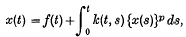
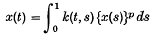
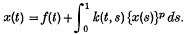
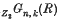 is strictly less than the maximum possible value dim
is strictly less than the maximum possible value dim  the number of possible derangements of the set i.e. permutations in which no object occupies a site originally occupied by an object of the same type. A formula is found for
the number of possible derangements of the set i.e. permutations in which no object occupies a site originally occupied by an object of the same type. A formula is found for 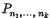 in terms of Laguerre polynomials, and some of its implications are considered.
in terms of Laguerre polynomials, and some of its implications are considered.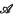 } it vectors such that, for each α, there is an hermitian (in the numerical range sense, see (4)) projection
} it vectors such that, for each α, there is an hermitian (in the numerical range sense, see (4)) projection 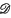 ′ (Ω) and
′ (Ω) and 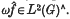 . Edwards has shown in (2) that
. Edwards has shown in (2) that 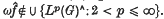 . We strengthen this result by showing much more can be said about the summability of the Fourier series of
. We strengthen this result by showing much more can be said about the summability of the Fourier series of 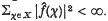 . For example, when
. For example, when