Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T14:30:19.849Z Has data issue: false hasContentIssue false
  • English
  • Français

Unbounded operators and random Fourier series

Published online by Cambridge University Press:  24 October 2008

J. W. Sanders
J. W. Sanders
Affiliation:
Australian National University
Get access Rights & Permissions [Opens in a new window]

Extract

0·0. Let G be an infinite compact abelian group with dual X. Parseval's identity shows that if f ∈ C(G) and ω ∈ l∞(X) then 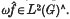. Edwards has shown in (2) that L2(G) here cannot, in general, be replaced by any smaller Lp(G) space. Precisely: there exist f ∈ C(G) and ω: X → {± 1} such that 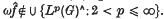. We strengthen this result by showing much more can be said about the summability of the Fourier series of f than 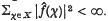. For example, when G is the circle group, f can be chosen to also satisfy

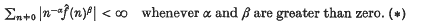
The functions introduced here and called darts, generalize this type of series condition.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 79 , Issue 3 , May 1976 , pp. 511 - 520
Copyright
Copyright © Cambridge Philosophical Society 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Edwards, R. E.Functional analysis. Theory and applications (New York; Holt, Rinehart and Winston, Inc., 1965).Google Scholar
(2)Edwards, R. E.Changing signs of Fourier coefficients. Pacific J. Math. 15 (1965), 463–475.CrossRefGoogle Scholar
(3)Gaudry, G. I.Changes of signs of restrictions of Fourier–Stieltjes transforms. Proc. Cambridge Philos. Soc. 66 (1969), 295–300.CrossRefGoogle Scholar
(4)Rudin, W.Fourier analysis on groups (New York; Interscience, 1962).Google Scholar
(5)Sanders, J. W.Weighted Sidon sets. Pacific J. Math. (to appear).Google Scholar