Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T14:39:48.763Z Has data issue: false hasContentIssue false
  • English
  • Français

Hilbert space methods in the theory of Jordan algebras. II

Published online by Cambridge University Press:  24 October 2008

C. Viola Devapakkiam  and
P. S. Rema
C. Viola Devapakkiam
Affiliation:
Arts College, Dindigul, Tamil Nadu and Ramanujan Institute, Madras
P. S. Rema
Affiliation:
Arts College, Dindigul, Tamil Nadu and Ramanujan Institute, Madras
Get access Rights & Permissions [Opens in a new window]

Extract

In this paper we consider the classification problem for separable special simple J*-algebras (cf. (8)). We show, using a result of Ancochea, that if 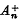is the (finite-dimensional) Jordan algebra of all complex n × n matrices and ø a Jordan isomorphism of 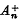onto a special J*-algebra J then An can be given the structure of an H*-algebra such that ø is a *-preserving isomorphism of the J*-algebra 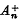onto J. This result enables us to construct explicitly a canonical basis for a finite-dimensional simple special J*-algebra isomorphic to a Jordan algebra of type I from which we also obtain canonical bases for special simple finite-dimensional J*-algebras isomorphic to Jordan algebras of type II and III.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 79 , Issue 2 , March 1976 , pp. 307 - 319
Copyright
Copyright © Cambridge Philosophical Society 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Ambrose, M.Structure theorem for a special class of Banach Algebras. Trans. Amer. Math. Soc. 57 (1945), 564–586.CrossRefGoogle Scholar
(2)Ancochea, G.On semi-automorphisme of divisor algebras. Ann. of Math. (2) 48 (1947), 147–153.Google Scholar
(3)Dunford, N. and Schwartz, J. T.Linear Operators, Part II (New York, Interscience, 1963).Google Scholar
(4)Jacobson, N. Structure and representations of Jordan algebras. Amer. Math. Soc. Coll. Pub. 39.Google Scholar
(5)Jacobson, N. and Jacobson, F. D.Classification and representation of semi-simple Jordan algebras. Trans. Amer. Math. Soc. 65 (1949), 141–169.CrossRefGoogle Scholar
(6)Kalisch, G. K.On special Jordan algebras. Trans. Amer. Math. Soc. 61 (1947), 482–494.CrossRefGoogle Scholar
(7)Schue, J. R.Hilbert space methods in the theory of Lie algebras. Trans. Amer. Math. Soc. 95 (1960), 69–80.Google Scholar
(8)Viola, Devapakkiam C.Hilbert space Methods in the theory of Jordan algebras. I. Math. Proc. Cambridge Philos. Soc. 78 (1975), 293–300.Google Scholar
(9)Viola, Devapakkiam C. Barach Jordan algebras. Doctoral Dissertation, University of Madras (1970).Google Scholar