Research Article
Banach–Mazur games, comeager sets and degrees of unsolvability
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 195-220
-
- Article
- Export citation
Maximal matchings in graphs with given minimal and maximal degrees
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 221-234
-
- Article
- Export citation
Groups of hyperbolic crystallography
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 235-249
-
- Article
- Export citation
Finite simple groups with Sylow 2-subgroups of type PSL(5, q), q odd
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 251-269
-
- Article
- Export citation
Automorphism sequences of free nilpotent groups of class two
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 271-279
-
- Article
- Export citation
Proof of a conjecture about the distribution of divisors of integers in residue classes
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 281-287
-
- Article
- Export citation
Läuchli's algebraic closure of Q
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 289-297
-
- Article
- Export citation
Three notes on proximity theory
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 299-305
-
- Article
- Export citation
Hilbert space methods in the theory of Jordan algebras. II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 307-319
-
- Article
- Export citation
Gleason parts for measure algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 321-327
-
- Article
- Export citation
On a class of Volterra and Fredholm non-linear integral equations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 329-335
-
- Article
- Export citation
The disintegration of invariant measures
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 337-341
-
- Article
- Export citation
A higher catastrophe machine
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 343-350
-
- Article
- Export citation
On a quantum mechanical model for a maser I†
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 351-371
-
- Article
- Export citation
Applications of Leray–Schauder degree theory to problems of hydrodynamic stability
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 373-392
-
- Article
- Export citation
Front matter
PSP volume 79 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 79 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation

 of degrees of unsolvability. A less obvious and more complicated extension of this framework has been initiated in our papers (17) and (18); these are concerned not with the general theory but with the Priority Method, for which a useful formal framework has long been sought. Our purpose here is partly to provide some background for these other papers, which should help explicate their less obvious aspects; but mainly we wish to illustrate the advantages of this framework from a purely expository point of view. There is an additional advantage in that a formal framework makes it possible to pose certain precise questions which were vague before, and even on occasion to answer them.
of degrees of unsolvability. A less obvious and more complicated extension of this framework has been initiated in our papers (17) and (18); these are concerned not with the general theory but with the Priority Method, for which a useful formal framework has long been sought. Our purpose here is partly to provide some background for these other papers, which should help explicate their less obvious aspects; but mainly we wish to illustrate the advantages of this framework from a purely expository point of view. There is an additional advantage in that a formal framework makes it possible to pose certain precise questions which were vague before, and even on occasion to answer them. . In this case,
. In this case, 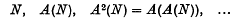
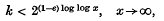
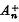 is the (finite-dimensional) Jordan algebra of all complex
is the (finite-dimensional) Jordan algebra of all complex