Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T02:33:46.607Z Has data issue: false hasContentIssue false
  • English
  • Français

Banach–Mazur games, comeager sets and degrees of unsolvability

Published online by Cambridge University Press:  24 October 2008

C. E. M. Yates
C. E. M. Yates
Affiliation:
University of Manchester
Get access Rights & Permissions [Opens in a new window]

Extract

This paper provides a framework for studying the general theory of the upper semi-lattice 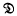of degrees of unsolvability. A less obvious and more complicated extension of this framework has been initiated in our papers (17) and (18); these are concerned not with the general theory but with the Priority Method, for which a useful formal framework has long been sought. Our purpose here is partly to provide some background for these other papers, which should help explicate their less obvious aspects; but mainly we wish to illustrate the advantages of this framework from a purely expository point of view. There is an additional advantage in that a formal framework makes it possible to pose certain precise questions which were vague before, and even on occasion to answer them.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 79 , Issue 2 , March 1976 , pp. 195 - 220
Copyright
Copyright © Cambridge Philosophical Society 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Harding, C. J. Ph.D. Thesis (Swansea 1975).Google Scholar
(2)Kleene, S. C. and Post, E. L.The upper semi lattice of degrees of recursive unsolvability. Ann. of Math. 59 (1954), 379–407.CrossRefGoogle Scholar
(3)Lachlan, A. H.Distributive initial segments of the degrees of unsolvability. Zeite. für Math. Logik und Grund. der Math. 14 (1969), 457–472.Google Scholar
(4)Lachlan, A. H.Solution to a problem of Spector. Can. J. Math. 23 (1971), 247–256.CrossRefGoogle Scholar
(5)Lachlan, A. H. and Lebeuf, R. Countable initial segments of the degrees of unsolvability (to appear).Google Scholar
(6)Lerman, M.Initial segments of the degrees of unsolvability. Ann. of Math. 93 (1971), 365–389.CrossRefGoogle Scholar
(7)Martin, D. A. Measure, category and dogrees of unsolvability (unpublished manuscript, 1967).Google Scholar
(8)Myhill, J.Category methods in recursion theory. Pacific J. Math. 11 (1961), 1479–1486.CrossRefGoogle Scholar
(9)Oxtoby, J. C.Measure and Category. Graduate Texts in Mathematics 2 (Springer-Verlag 1971).CrossRefGoogle Scholar
(10)Rogers, H. Jr, Theory of recursive functions and effective computability (McGraw-Hill 1967).Google Scholar
(11)Sacks, G. E.Degrees of Unsolvability (Annals of Mathematics Study no. 55, Princeton 1963, second edition 1966).Google Scholar
(12)Tthomason, S. K.On initial segments of hyperdegrees. J. Symb. Logic 35 (1970), 189–197.CrossRefGoogle Scholar
(13)Yayes, C. E. M.Density and incomparability in the degrees less than 0(1). (Abstract), J. Symb. Logic 31 (1966), 301–302.Google Scholar
(14)Yates, C. E. M. Initial segments of the degrees of unsolvability, Part I: A survey. Mathematical Logic and the Foundations of Set Theory, North-Holland 1970, 63–83.Google Scholar
(15)Yates, C. E. M.Initial segments of the degrees of unsolvability, Part II: Minimal degrees. J. Symb. Logic 35 (1970), 243–266.CrossRefGoogle Scholar
(16)Yates, C. E. M. Initial segments and implications for the structure of degrees. Conference in Mathematical Logic - London70 (Springer Lecture Notes 255, 1972), 305–335.CrossRefGoogle Scholar
(17)Yates, C. E. M. A general framework for simple and priority arguments. Proc. Int. Cong. of Math. (Vancouver 1974).Google Scholar
(18)Yates, C. E. M. Priorcomeager sets and degrees of unsolvability (in preparation).Google Scholar
(19)Yates, C. E. M.Degrees of unsolvability – a new approach(to appear in the Springer-Verlag series ‘Perspectives in Logic’).Google Scholar