Research Article
Finitude simple et structures o-minimales (Finiteness property implies o-minimality)
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1616-1622
-
- Article
- Export citation
Rangs et types de rang maximum dans les corps différentiellement clos
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1178-1188
-
- Article
- Export citation
More undecidable lattices of Steinitz exchange systems
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 859-878
-
- Article
- Export citation
An axiomatic presentation of the nonstandard methods in mathematics
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 315-325
-
- Article
- Export citation
Frege's unofficial arithmetic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1623-1638
-
- Article
- Export citation
The relation of recursive isomorphism for countable structures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 879-895
-
- Article
- Export citation
Theories with equational forking
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 326-340
-
- Article
- Export citation
On Lascar rank and Morley rank of definable groups in differentially closed fields
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1189-1196
-
- Article
- Export citation
Core models with more Woodin cardinals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1197-1226
-
- Article
- Export citation
Errata
Errata
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 1639
-
- Article
-
- You have access
- Export citation
Research Article
Open questions in the theory of spaces of orderings
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 341-352
-
- Article
- Export citation
Front matter
JSL volume 67 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. f1-f2
-
- Article
-
- You have access
- Export citation
JSL Volume 67 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
A classification of intersection type systems
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 353-368
-
- Article
- Export citation
Back matter
JSL volume 67 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Research Article
Sequences of n-diagrams
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1227-1247
-
- Article
- Export citation
Back matter
JSL Volume 67 issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. b1-b10
-
- Article
-
- You have access
- Export citation
Other
Notice from the editors
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 1248
-
- Article
- Export citation
Research Article
On essentially low, canonically well-generated Boolean algebras
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 369-396
-
- Article
- Export citation
Front matter
JSL Volume 67 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. f1-f2
-
- Article
-
- You have access
- Export citation

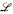
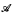 of
of 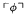 of
of 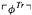 is a second-order sentence containing no arithmetical vocabulary, and
is a second-order sentence containing no arithmetical vocabulary, and 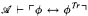
 ,
, ,
,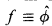 mod Cont(
mod Cont(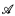 , the complete (elementary) diagram,
, the complete (elementary) diagram, 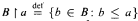 . The rank of 0
. The rank of 0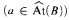 , if the last nonzero cardinal in the cardinal sequence of
, if the last nonzero cardinal in the cardinal sequence of 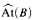 . We denote
. We denote 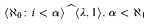 . If
. If