Research Article
On iterating semiproper preorders
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1431-1468
-
- Article
- Export citation
SN and CR for free-style LKtq: linear decorations and simulation of normalization
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 162-196
-
- Article
- Export citation
On orbits, of prompt and low computably enumerable sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 649-678
-
- Article
- Export citation
Representability in second-order propositional poly-modal logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1039-1054
-
- Article
- Export citation
Relation algebra reducts of cylindric algebras and an application to proof theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 197-213
-
- Article
- Export citation
Definable incompleteness and Friedberg splittings
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 679-696
-
- Article
- Export citation
A rank for the class of elementary submodels of a superstable homogeneous model
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1469-1482
-
- Article
- Export citation
Isolation and lattice embeddings
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1055-1064
-
- Article
- Export citation
Degree spectra of relations on computable structures in the presence of Δ20 isomorphisms
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 697-720
-
- Article
- Export citation
The strict order property and generic automorphisms
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 214-216
-
- Article
- Export citation
The lazy logic of partial terms
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1065-1077
-
- Article
- Export citation
A unified completeness theorem for quantified modal logics
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1483-1510
-
- Article
- Export citation
A constructive look at the completeness of the space
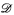 (ℝ)
(ℝ)
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1511-1519
-
- Article
- Export citation
Two cardinal properties of homogeneous graphs
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 217-220
-
- Article
- Export citation
Generalized r-cohesiveness and the arithmetical hierarchy: a correction to “Generalized cohesiveness”
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1078-1082
-
- Article
- Export citation
Deconstructing inner model theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 721-736
-
- Article
- Export citation
Compact complex manifolds with the DOP and other properties
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 737-743
-
- Article
- Export citation
A dichotomy theorem for turbulence
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1520-1540
-
- Article
- Export citation
Strong convergence in finite model theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1083-1092
-
- Article
- Export citation
On modal logics between K × K × K and S5 × S5 × S5
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 221-234
-
- Article
- Export citation

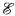 of computably enumerable sets under inclusion, and prove that
of computably enumerable sets under inclusion, and prove that 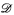 (ℝ)
(ℝ)
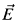 of extenders as in [2]. Condensation results have the general form: if
of extenders as in [2]. Condensation results have the general form: if 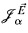 , then either
, then either 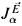 , or else from
, or else from 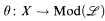
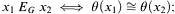
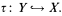
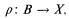
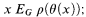
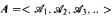 of finite models, where the universe of
of finite models, where the universe of  , is {1,2,…,
, is {1,2,…,