Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T07:03:32.493Z Has data issue: false hasContentIssue false
  • English
  • Français

Deconstructing inner model theory

Published online by Cambridge University Press:  12 March 2014

Ralf-Dieter Schindler ,
John Steel  and
Martin Zeman
Ralf-Dieter Schindler
Affiliation:
Institut für Formale Logik, Universität Wien, Wahringer Str. 25, 1090 Wien, Austria, E-mail: [email protected]
John Steel
Affiliation:
Department of Mathematics, UC Berkeley, Berkeley, California 94720, USA, E-mail: [email protected]
Martin Zeman
Affiliation:
Institut für Formale Logik, Universität Wien, Währinger Str. 25, 1090 Wien, Austria Mathematical Institute Sav, Štefánikova 49, 1814 73 Bratislava, Slovak Republic, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

In this paper we shall repair some errors and fill some gaps in the inner model theory of [2]. The problems we shall address affect some quite basic definitions and proofs.

We shall be concerned with condensation properties of canonical inner models constructed from coherent sequences 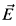of extenders as in [2]. Condensation results have the general form: if x is definable in a certain way over a level , then either x ∈ 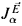, or else from x we can reconstruct in a simple way.

The first condensation property considered in [2] is the initial segment condition, or ISC. In section 1 we show that the version of this condition described in [2] is too strong, in that no coherent 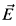in which the extenders are indexed in the manner of [2], and which is such that L[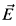] satisfies the mild large cardinal hypothesis that there is a cardinal which is strong past a measurable, can satisfy the full ISC of [2]. It follows that the coherent sequences constructed in [2] do not satisfy the ISC of [2]. We shall describe the weaker ISC which these sequences do satisfy, and indicate the small changes in the arguments of [2] this new condition requires.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 67 , Issue 2 , June 2002 , pp. 721 - 736
Copyright
Copyright © Association for Symbolic Logic 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Jensen, Ronald, A new fine structure for higher core models, handwritten notes.Google Scholar
[2]Mitchell, William and Steel, John, Fine structure and iteration trees, Lecture Notes in Logic, vol. 3, Springer-Verlag, 1994.CrossRefGoogle Scholar
[3]Neeman, Itay and Steel, John, A weak Dodd-Jensen lemma, this Journal, vol. 64 (1999). pp. 1285–1294.Google Scholar
[4]Schimmerling, Ernest, Combinatorial principles in the core model for one Woodin cardinal, Annals of Pure and Applied Logic, vol. 74 (1995), pp. 153–201.CrossRefGoogle Scholar
[5]Steel, John, The core model iterability problem, Lecture Notes in Logic, vol. 8, Springer-Verlag, 1996.CrossRefGoogle Scholar