Research Article
Local superssimplicity and related concepts
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 744-758
-
- Article
- Export citation
On polynomial time computation over unordered structures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1093-1125
-
- Article
- Export citation
A model-theoretic proof for P ≠ NP over all infinite abelian group
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 235-238
-
- Article
- Export citation
Modulated fibring and the collapsing problem
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1541-1569
-
- Article
- Export citation
The torsionfree part of the Ziegler spectrum of RG when R is a Dedekind domain and G is a finite group
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1126-1140
-
- Article
- Export citation
Minimal groups in separably closed fields
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 239-259
-
- Article
- Export citation
On Dipphantine definability and decidability in some rings of algebraic functions of characteristic 0
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 759-786
-
- Article
- Export citation
Borovik-Poizat rank and stability
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1570-1578
-
- Article
- Export citation
Contiguity and distributivity in the enumerable Turing degrees — Corrigendum
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1579-1580
-
- Article
- Export citation
Bounded Martin's Maximum, weak Erdӧs cardinals, and ψAc
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1141-1152
-
- Article
- Export citation
Wellordering proofs for metapredicative Mahlo
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 260-278
-
- Article
- Export citation
Generalised weak presentations
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 787-819
-
- Article
- Export citation
Indestructibility and the level-by-level agreement between strong compactness and supercompactness
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 820-840
-
- Article
- Export citation
Transfinite dependent choice and ω-model reflection
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1153-1168
-
- Article
- Export citation
Group configurations and germs in simple theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1581-1600
-
- Article
- Export citation
Proving consistency of equational theories in bounded arithmetic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 279-296
-
- Article
- Export citation
Modular types in some supersimple theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1601-1615
-
- Article
- Export citation
Modules with few types over some finite-dimensional algebras
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 841-858
-
- Article
- Export citation
The relative consistency of g < cf(Sym(ω))
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 297-314
-
- Article
- Export citation
On regular reduced products*
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1169-1177
-
- Article
- Export citation

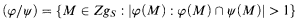
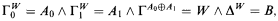
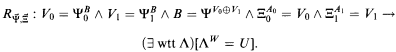
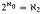 . We also prove that
. We also prove that 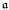 . is there an injective map
. is there an injective map 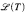 of cardinality ≤
of cardinality ≤