Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-12-03T19:11:23.068Z Has data issue: false hasContentIssue false
  • English
  • Français

The torsionfree part of the Ziegler spectrum of RG when R is a Dedekind domain and G is a finite group

Published online by Cambridge University Press:  12 March 2014

A. Marcja ,
M. Prest  and
C. Toffalori
A. Marcja
Affiliation:
Dipartimento Di Matematica, U. Dini, Università Di Firenze, Viale Morgagni 67/A, 1-50134 Firenze, Italy, E-mail: [email protected]
M. Prest
Affiliation:
Department of Mathematics, University of Manchester, Oxford Road, Manchester M13 9PL, England, E-mail: [email protected]
C. Toffalori
Affiliation:
Dipartimento Di Matematica E Infomatica, Università Di Camerino, Via Madonna Delle Carceri, 1-62032 Camerino, Italy, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

For every ring S with identity, the (right) Ziegler spectrum of S, Zgs, is the set of (isomorphism classes of) indecomposable pure injective (right) S-modules. The Ziegler topology equips Zgs with the structure of a topological space. A typical basic open set in this topology is of the form

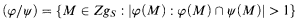
where φ and ψ are pp-formulas (with at most one free variable) in the first order language Ls for S-modules; let [φ/ψ] denote the closed set Zgs - (φ/ψ). There is an alternative way to introduce the Ziegler topology on Zgs. For every choice of two f.p. (finitely presented) S-modules A, B and an S-module homomorphism f: A → B, consider the set (f) of the points N in Zgs such that some S-homomorphism h: A → N does not factor through f. Take (f) as a basic open set. The resulting topology on Zgs is, again, the Ziegler topology.

The algebraic and model-theoretic relevance of the Ziegler topology is discussed in [Z], [P] and in many subsequent papers, including [P1], [P2] and [P3], for instance. Here we are interested in the Ziegler spectrum ZgRG of a group ring RG, where R is a Dedekind domain of characteristic 0 (for example R could be the ring Z of integers) and G is a finite group. In particular we deal with the R-torsionfree points of ZgRG.

The main motivation for this is the study of RG-lattices (i.e., finitely generated R-torsionfree RG-modules).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 67 , Issue 3 , September 2002 , pp. 1126 - 1140
Copyright
Copyright © Association for Symbolic Logic 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[BT]Baratella, S. and Toffalori, C., The theory of ZC (2)2-lattices is decidable, Archive of Mathematical Logic, vol. 37 (1998), pp. 91–104.CrossRefGoogle Scholar
[CR]Curtis, C. and Reiner, I., Methods of representation theory with applications to finite groups and orders I, Wiley, New York, 1981.Google Scholar
[J]Jacobson, N., Basic algebra II, W. H. Freeman, San Francisco, 1980.Google Scholar
[MT]Marcja, A. and Toffalori, C., Decidable representations, Journal of Pure and Applied Algebra, vol. 103 (1995), pp. 189–203.CrossRefGoogle Scholar
[P]Prest, M., Model theory and modules, Cambridge University Press, Cambridge, 1988.CrossRefGoogle Scholar
[P2]Prest, M., The Zariski spectrum of the category of finitely presented modules, preprint, 1998.Google Scholar
[P1]Prest, M., Ziegler spectra of tame hereditary algebras, Journal of Algebra, vol. 207 (1998), pp. 146–164.CrossRefGoogle Scholar
[P3]Prest, M., Topological and geometric aspects of the Ziegler spectrum, Infinite length modules (Krause, H. and Ringel, C. M., editors), Birkhäuser, 2000, pp. 369–392.CrossRefGoogle Scholar
[Roth]Rothmaler, Ph., Purity in model theory, Advances in algebra and model theory, Algebra, Logic and Applications, vol. 9, Gordon and Breach, Amsterdam, 1997, pp. 445–469.Google Scholar
[T]Toffalori, C., Wildness implies undecidability for lattices over group rings, this Journal, vol. 63 (1997), pp. 1429–1447.Google Scholar
[T1]Toffalori, C., The decision problem for ZC(p3)-lattices with p prime, Archive of Mathematical Logic, vol. 37 (1998), pp. 127–142.CrossRefGoogle Scholar
[Z]Ziegler, M., Model theory of modules, Annals of Pure and Applied Logic, vol. 26 (1984), pp. 149–213.CrossRefGoogle Scholar