Published online by Cambridge University Press: 12 March 2014
Spaces of orderings provide an abstract framework in which to study spaces of orderings of formally real fields. Spaces of orderings of finite chain length are well understood [9, 11]. The Isotropy Theorem [11] and the extension of the Isotropy Theorem given in [13] are the main tools for reducing questions to the finite case, and these are quite effective. At the same time, there are many questions which do not appear to reduce in this way. In this paper we consider four such questions, for a space of orderings (X, G).
1. Is it true that every positive primitive formula P(a) with parameters a in G which holds in every finite subspace of (X, G) necessarily holds in (X, G)?
2. If f: X → ℤ is continuous and Σx∈Vf(x) ≡ 0 mod ∣V∣ holds for all fans V in X with ∣V∣ ≤ 2n, does there exist a form ϕ with entries in G such that 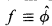 mod Cont(X, 2nℤ)?
mod Cont(X, 2nℤ)?
3. Is it true that Cont(X, 2nℤ) ∩ Witt(X, G) = In(X, G), where I(X, G) denotes the fundamental ideal?
4. Is the separating depth of a constructible set C in X necessarily bounded by the stability index of (X, G)?
The unexplained terminology and notation is explained later in the main body of the paper. In a certain sense Question 1 is the main question. At the same time, Questions 2, 3 and 4 are of considerable interest, both from the point of view of quadratic form theory and from the point of view of real algebraic geometry.