Research Article
Weight ω in stable theories with few types
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 353-373
-
- Article
- Export citation
Determinacy and the sharp function on objects of type k
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1025-1053
-
- Article
- Export citation
A combinatorial forcing for coding the universe by a real when there are no sharps
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1-35
-
- Article
- Export citation
Generic trees
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 705-726
-
- Article
- Export citation
Martin's axiom and the continuum
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 374-391
-
- Article
- Export citation
Degree theoretic definitions of the low2 recursively enumerable sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 727-756
-
- Article
- Export citation
Storage operators and directed lambda-calculus
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1054-1086
-
- Article
- Export citation
The combinatorics of combinatorial coding by a real
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 36-57
-
- Article
- Export citation
The bounded proper forcing axiom
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 58-73
-
- Article
- Export citation
The dimension of the negation of transitive closure
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 392-414
-
- Article
- Export citation
The syntax and semantics of entailment in duality theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1087-1114
-
- Article
- Export citation
The finite model property in tense logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 757-774
-
- Article
- Export citation
The axiom of choice for well-ordered families and for families of well-orderable sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1115-1117
-
- Article
- Export citation
T-convexity and tame extensions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 74-102
-
- Article
- Export citation
Perfect extensions and derived algebras
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 775-796
-
- Article
- Export citation
Ultrafilters generated by a closed set of functions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 415-430
-
- Article
- Export citation
Delineating classes of computational complexity via second order theories with weak set existence principles. I
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 103-121
-
- Article
- Export citation
On the equivalence of certain consequences of the proper forcing axiom
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 431-443
-
- Article
- Export citation
The undecidability of the Π4-theory for the r.e. wtt and Turing degrees
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1118-1136
-
- Article
- Export citation
Defining multiplication in o-minimal expansions of the additive reals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 797-816
-
- Article
- Export citation

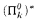 and
and 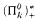 , which lie strictly between
, which lie strictly between 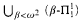 and
and 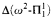 . Let #
. Let #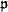 < add(
< add(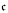 =
= 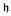 . We show that
. We show that 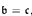 ,
, 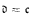 implies cov(ℓ
implies cov(ℓ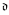 holds. Finally we prove that Cohen forcing does not add a superperfect tree of Cohen reals.
holds. Finally we prove that Cohen forcing does not add a superperfect tree of Cohen reals.
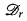 of the
of the 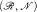 with ℛ a model of
with ℛ a model of 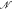 a proper elementary substructure that is Dedekind complete in ℛ. We deduce that the theory of such “tame” pairs is complete.
a proper elementary substructure that is Dedekind complete in ℛ. We deduce that the theory of such “tame” pairs is complete.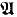 can be extended to a complete and atomic Bo satisfying certain additional conditions, and that any two complete, atomic extensions of
can be extended to a complete and atomic Bo satisfying certain additional conditions, and that any two complete, atomic extensions of 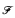 a filter on
a filter on 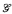 a set of functions from
a set of functions from 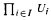 such that, for all
such that, for all 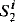 (Lemmas 4 and 5). Our proofs use a technique which enables us to “speed up” induction without increasing the bounded complexity of the induction formulas. This technique is also used to obtain an interpretability result for the theories of bounded arithmetic
(Lemmas 4 and 5). Our proofs use a technique which enables us to “speed up” induction without increasing the bounded complexity of the induction formulas. This technique is also used to obtain an interpretability result for the theories of bounded arithmetic 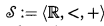 —the ordered additive reals. More particularly we consider the case when the expansions are “eventually nonlinear” (see below), and find that multiplication is actually definable in all cases except when the structure is “eventually almost linear”, which is a rare special case in which multiplication is obviously not definable. Thus the main theorem established is:
—the ordered additive reals. More particularly we consider the case when the expansions are “eventually nonlinear” (see below), and find that multiplication is actually definable in all cases except when the structure is “eventually almost linear”, which is a rare special case in which multiplication is obviously not definable. Thus the main theorem established is: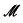 an o-minimal expansion of
an o-minimal expansion of 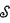 , if
, if