Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-19T00:21:49.844Z Has data issue: false hasContentIssue false
  • English
  • Français

Martin's axiom and the continuum

Published online by Cambridge University Press:  12 March 2014

Haim Judah  and
Andrzej Rosłanowski
Haim Judah
Affiliation:
Abraham Frankel Center for Mathematical Logic, Department of Mathematics and Computer Science, Bar-Ilan University, 52900 Ramat-Gan, Israel, E-mail: [email protected]
Andrzej Rosłanowski
Affiliation:
Institute of Mathematics, Hebrew University of Jerusalem, 91904 Jerusalem, Israel Mathematical Institute, Wrocław University, 50384 Wrocław, Poland, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

Since Georg Cantor discovered set theory the main problem in this area of mathematical research has been to discover what is the size of the continuum. The continuum hypothesis (CH) says that every infinite set of reals either has the same cardinality as the set of all reals or has the cardinality of the set of natural numbers, namely

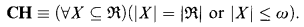
In 1939 Kurt Gödel discovered the Constructible Universe and proved that CH holds in it. In the early sixties Paul Cohen proved that every universe of set theory can be extended to a bigger universe of set theory where CH fails. Moreover, given any reasonable cardinal κ, it is possible to build a model where the continuum size is κ. The new technique discovered by Cohen is called forcing and is being used successfully in other branches of mathematics (analysis, algebra, graph theory, etc.).

In the light of these two stupendous works the experts (especially the platonists) were forced to conclude that from the point of view of the classical axiomatization of set theory (called ZFC) it is impossible to give any answer to the continuum size problem: everything is possible!

In private communications Gödel suggested that the continuum size from a platonistic point of view should be ω2, the second uncountable cardinal. As this is not provable in ZFC, Gödel suggested that a new axiom should be added to ZFC to decide that the cardinality of the continuum is ω2.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 60 , Issue 2 , June 1995 , pp. 374 - 391
Copyright
Copyright © Association for Symbolic Logic 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[BFS] Brendle, J., Judah, H., and Shelah, S., Combinatorial properties of Heckler forcing, Annals of Pure and Applied Logic, vol. 58 (1992), pp. 185–199.CrossRefGoogle Scholar
[DF] Van Douwen, E. K. and Fleissner, W. G., Definable forcing axiom: an alternative to Martin's axiom, Topology and Its Applications, vol. 35 (1990), pp. 277–289.CrossRefGoogle Scholar
[GJS] Goldstern, M., Judah, H., and Shelah, S., Strong measure zero sets without Cohen reals, this Journal, vol. 58 (1993), pp. 1323–1341.Google Scholar
[HS] Harrington, L. and Shelah, S., Some exact equiconsistency results in set theory, Notre Dame Journal of Formal Logic, vol. 26 (1985), pp. 178–188.CrossRefGoogle Scholar
[Jec] Jech, T., Set theory, Academic Press, New York, 1978.Google Scholar
[Ju] Judah, H., Was Gödel right?, Notes, Mathematical Sciences Research Institute, Berkeley, California, 1989.Google Scholar
[JRS] Judah, H., Rosłanowski, A, and Shelah, S., Examples for Souslin forcing, Fundamenta Mathematicae, vol. 144 (1994), pp. 23–42.CrossRefGoogle Scholar
[JS] Judah, H. and Shelah, S., Souslin forcing, this Journal, vol. 53 (1988), pp. 1182–1207.Google Scholar
[JS2] Judah, H. and Shelah, S., Souslin absoluteness, preprint.Google Scholar
[JS3] Judah, H. and Shelah, S., Martin's axioms, measurability and equiconsistency results, this Journal, vol. 54 (1989), pp. 78–94.Google Scholar
[MP] Miller, A. and Prikry, K., When the continuum has cofinality ω1, Pacific Journal of Mathematics, vol. 115 (1984), pp. 399–407.CrossRefGoogle Scholar
[MS] Martin, D. A. and Solovay, R. M., Internal Cohen extensions, Annals of Mathematical Logic, vol. 2 (1970), pp. 143–178.CrossRefGoogle Scholar
[Ra] Raisonnier, J., A mathematical proof of S. Shelah's theorem on the measure problem and related results, Israel Journal of Mathematics, vol. 48 (1984), pp. 48–56.CrossRefGoogle Scholar
[RS1] Roslanowski, A. and Shelah, S., More forcing notions imply diamonds, Archive for Mathematical Logic (to appear).Google Scholar
[RS2] Rosłanowski, A. and Shelah, S., Simple forcing notions and forcing axioms, preprint.Google Scholar
[Sh1] Shelah, S., How special are Cohen and random forcings, Israel Journal of Mathematics, vol. 88 (1994), pp. 153–174.Google Scholar
[Sh2] Shelah, S., Proper forcing, Lecture Notes in Mathematics, vol. 940, Springer-Verlag, Berlin, 1982.CrossRefGoogle Scholar
[Si] Sikorski, R., Boolean algebras, 2nd ed., Springer-Verlag, Berlin, 1964.Google Scholar
[T] Todorčević, S., Remarks on Martin's axiom and the continuum hypothesis, Canadian Journal of Mathematics, vol. 43 (1991), pp. 832–851.CrossRefGoogle Scholar
[Ve] Veličković, B., Forcing axioms and stationary sets, Advances in Mathematics, vol. 94 (1992), pp. 256–284.CrossRefGoogle Scholar