In treatises or advanced textbooks on theoretical physics, it is apparent that the way mathematics is used is very different from what is to be found in books of mathematics. There is, for example, no close connection between books on analysis, on the one hand, and any classical textbook in quantum mechanics, for example, Schiff, [11], or quite recent books, for example Ryder, [10], on quantum field theory. The differences run a good deal deeper than the fact that the books on theoretical physics are not written in the definition-theorem-proof style characteristic of pure mathematics. Although a good many propositions are proved in the books on physics, there are almost with exception no existential proofs, and consequently there is no really serious systematic use of quantifiers. Another important characteristic is the free use of infinitesimals. In fact, most results would not lose anything, from a physicist's point of view, by leaving them in approximate form, i.e., instead of strict equalities or inequalities, using equalities or inequalities only up to an infinitesimal.

The discrepancy between the way mathematics is ordinarily done in theoretical physics and the way it is built up from a foundational standpoint in any of the standard modern views raises the question of whether it might be possible to construct quite directly a rigorous foundation that reflects a significant part of this standard practice in theoretical physics. Other parts of standard practice in physics, for example, the use of physically intuitive but nonrigorous arguments, are not present in our system.

We define a σ-ideal on the set of functions ωω with the property that a real x ∈ ωω is a Hechler real over V if and only if x omits all Borel sets in . In fact we define a topology on ωω related to Hechler forcing such that is the family of first category sets in . We study cardinal invariants of the ideal .

Some methods of constructing nonstandard models work only for particular theories, such as ZFC, or CA + AC (which is second order number theory with the choice scheme). The examples of this which motivated the results of this paper occur in the main theorems of [5], which state that if T is any consistent extension of either ZFC0 (which is ZFC but with only countable replacement) or CA + AC and if κ and λ are suitably chosen cardinals, then T has a model which is κ-saturated and has the λ-Bolzano-Weierstrass property. (Compare with Theorem 3.5.) Another example is a result from [12] which states that if T is any consistent extension of CA + AC and cf (λ) > ℵ0, then T has a natural λ-Archimedean model. (Compare with Theorem 3.1 and the comments following it.) Still another example is a result in [6] in which it is shown that if a model of Peano arithmetic is expandable to a model of ZF or of CA, then so is any cofinal extension of . (Compare with Theorem 3.10.) Related types of constructions can also be found in [10] and [11].

A reflection principle will be proved here, allowing these constructions to be extended to models of many other theories, among which are some exceedingly weak theories and also all of their completions.

We study o-minimal expansions of Archimedean totally ordered groups. We first prove that any such expansion must be elementarily embeddable via a unique (provided some nonzero element is 0-definable) elementary embedding into a unique o-minimal expansion of the additive ordered group of real numbers . We then show that a definable function in an o-minimal expansion of enjoys good differentiability properties and use this to prove that an Archimedean real closed field is definable in any nonsemilinear expansion of . Combining these results, we obtain several restrictions on possible o-minimal expansions of arbitrary Archimedean ordered groups and in particular of the rational ordered group.

The present article, which is a revised version of part of [Hu1], deals with various relations between models which might serve as exact formulations for the vague concept “similar” or “almost isomorphic”. One natural class of such formulations is equivalence in a given logic. Another way to express similarity is by potential isomorphism, i.e., isomorphism in some extension of the set-theoretic universe. The class of extensions may be restricted to give different notions of potential isomorphism. A third method is to study the winning strategies for an Ehrenfeucht-Fraïssé-game played between the two models, and the properties of the resulting equivalence and nonequivalence trees.

The basic question studied here is whether one such notion of similarity implies another. Some implications and counterexamples listed in this part are previously known or trivial, but all are mentioned for completeness' sake. Only models of cardinality ℵ1 are considered. Some results are therefore connected with the Continuum Hypothesis.

We are accustomed to regarding K as the weakest modal logic admitting of a relational semantics in the style made popular by Kripke. However, in a series of papers which demonstrates a startling connection between modal logic and the theory of paraconsistent inference, Ray Jennings and Peter Schotch have developed a generalized relational frame theory which articulates an infinite hierarchy of sublogics of K, each expressing a species of “weakly aggregative necessity”. Recall that K is axiomatized, in the presence of N and RM, by the schema of “binary aggregation”

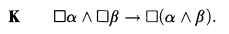
For each n ≥ 1, the weakly aggregative modal logic Kn is axiomatized by replacing K with the schema of “n-ary aggregation”

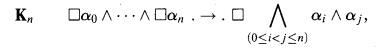
which is an n-ary relaxation, or weakening, of K. Note that K1 = K.

In [3], the authors claim without proof that Kn is determined by the class of frames F = (W, R), where W is a nonempty set and R is an (n + 1)-ary relation on W, under the generalization of Kriple's truth condition according to which □α is true at a point w in W if and only if α is true at one of x1,…,xn for all x1,…, xn in W such that Rw, x1,…, xn.

An ordered field is said to be Scott complete iff it is complete with respect to its uniform structure. Zakon has asked whether nonstandard real lines are Scott complete. We prove in ZFC that for any complete Boolean algebra B which is not (ω, 2)-distributive there is an ultrafilter of B such that the Boolean ultrapower of the real line modulo is not Scott complete. We also show how forcing in set theory gives rise to examples of Boolean ultrapowers of the real line which are not Scott complete.

We present in this paper an axiomatization of Belnap and Perloff's stit theory (a logic of “seeing to it that”) with a single agent. The idea of the proof is to apply the notion of companion sets—the same notion as used in another paper by the author that showed the decidability of stit theory with a single agent and Refref equivalence.

We study first-order properties of the quotient rings (V)/ by a prime ideal where (V) is the ring of p-adic valued continuous definable functions on some affine p-adic variety V. We show that they are integrally closed Henselian local rings, with a p-adically closed residue field and field of fractions, and they are not valuation rings in general but always satisfy ∀ x, y(x∣y2 ∨ y∣x2).

We present a canonical form for definable subsets of algebraically closed valued fields by means of decompositions into sets of a simple form, and do the same for definable subsets of real closed valued fields. Both cases involve discs, forming “Swiss cheeses” in the algebraically closed case, and cuts in the real closed case. As a step in the development, we give a proof for the fact that in “most” valued fields F, if f(x), g(x) ∈ F[x] and v is the valuation map, then the set {x: v(f(x)) ≤ v(g(x))} is a Boolean combination of discs; in fact, it is a finite union of Swiss cheeses. The development also depends on the introduction of “valued trees”, which we define formally.

We define the ideal with the property that a real omits all Borel sets in the ideal which are coded in a transitive model if and only if it is an amoeba real over this model. We investigate some other properties of this ideal. Strolling through the "amoeba forest" we gain as an application a modification of the proof of the inequality between the additivities of Lebesgue measure and Baire category.

The paper “Partitions of Products” [DiPH] investigated the polarized partition relation

The relation is consistent relative to an inaccessible cardinal if every αi is finite, but inconsistent if two are infinite. We show here that it consistent (relative to an inaccessible) for one to be infinite.

Along the way, we prove an interesting proposition from ZFC concerning partitions of the finite subsets of ω.

Pretopologies were introduced in [S], and there shown to give a complete semantics for a propositional sequent calculus BL, here called basic linear logic, as well as for its extensions by structural rules, ex falso quodlibet or double negation. Immediately after Logic Colloquium '88, a conversation with Per Martin-Löf helped me to see how the pretopology semantics should be extended to predicate logic; the result now is a simple and fully constructive completeness proof for first order BL and virtually all its extensions, including the usual, or structured, intuitionistic and classical logic. Such a proof clearly illustrates the fact that stronger set-theoretic principles and classical metalogic are necessary only when completeness is sought with respect to a special class of models, such as the usual two-valued models.

To make the paper self-contained, I briefly review in §1 the definition of pretopologies; §2 deals with syntax and §3 with semantics. The completeness proof in §4, though similar in structure, is sensibly simpler than that in [S], and this is why it is given in detail. In §5 it is shown how little is needed to obtain completeness for extensions of BL in the same language. Finally, in §6 connections with proofs with respect to more traditional semantics are briefly investigated, and some open problems are put forward.

An ω-model (a model in which all natural numbers are standard) of the predicative fragment of Quine's set theory “New Foundations” (NF) is constructed. Marcel Crabbé has shown that a theory NFI extending predicative NF is consistent, and the model constructed is actually a model of NFI as well. The construction follows the construction of ω-models of NFU (NF with urelements) by R. B. Jensen, and, like the construction of Jensen for NFU, it can be used to construct α-models for any ordinal α. The construction proceeds via a model of a type theory of a peculiar kind; we first discuss such “tangled type theories” in general, exhibiting a “tangled type theory” (and also an extension of Zermelo set theory with Δ0 comprehension) which is equiconsistent with NF (for which the consistency problem seems no easier than the corresponding problem for NF (still open)), and pointing out that “tangled type theory with urelements” has a quite natural interpretation, which seems to provide an explanation for the more natural behaviour of NFU relative to the other set theories of this kind, and can be seen anachronistically as underlying Jensen's consistency proof for NFU.

We establish a course-of-values induction principle for K-finite sets in intuitionistic type theory. Using this principle, we prove a pigeonhole principle conjectured by Bénabou and Loiseau. We also comment on some variants of this pigeonhole principle.

A definition is given for formulae A1, …, An in some theory T which is formalized in a propositional calculus S to be (in)dependent with respect to S. It is shown that, for intuitionistic propositional logic IPC, dependency (with respect to IPC itself) is decidable. This is an almost immediate consequence of Pitts’ uniform interpolation theorem for IPC. A reasonably simple infinite sequence of IPC-formulae Fn (p, q) is given such that IPC-formulae A and B are dependent if and only if at least on of the Fn (A, B) is provable.

Let be a finitely presented variety with operations Ω and let be the variety having the same set of operations Ω but defined by the empty set of identities. A partial-algebra is a set P with a set of mappings containing for each n-ary operation f of Ω a mapping , where D ⊆ Pn. An incomplete -algebra is a partial -algebra which satisfies the defining identities of , insofar as they can be applied to the partial operations of (Trevor Evans [4, p. 67]). We call an incomplete -algebra a partial Evans-algebra if it can be embedded in a member of the variety .

If the class of all partial Evans -algebras is (first-order) finitely axiomatizable, then the word problem for the variety is solvable. (Evans [4, 5]). In 1953 Evans [5, p. 79] raised the question of whether the converse is true. In this paper we show that the answer is in the negative.

Let CSg denote the variety of commutative semigroups. We call an incomplete CSg-algebra an incomplete commutative semigroup and we call a partial Evans CSg-algebra a partial Evans commutative semigroup. It is known (A. I. Malcev [9] see also Evans [6]) that the variety of commutative semigroups has solvable word problem. We show (Theorem 1) that the class of all partial Evans commutative semigroups is not finitely axiomatizable. Therefore the solvability of the word problem for the variety of commutative semigroups does not imply finite axiomatizability of the class of all partial Evans commutative semigroups.

Let P− denote the Peano axioms minus the induction scheme. Let IΣn, (I∏n), BΣn (B∏n), LΣn (L∏n denote the induction scheme, the collection scheme, and the least number principle for Σn-(∏n-) formulas respectively. Paris and Kirby [3] studied the relative proof-theoretic strengths of those schemes. The general theorem states that IΣn, I∏n, LΣn, and L∏n are equivalent; IΣn implies BΣn implies IΣn–1; but not conversely.

In recent years, people have been interested in doing recursion theory on fragments of arithmetic. One of the purposes of this study is to understand the priority methods. Much work has been done in this area. For example, M. Mytilinaios [5] showed that the Sacks splitting theorem can be proven in P− + IΣ1. Later, J. Mourad showed that the Sacks splitting theorem is indeed equivalent to IΣ1 [4]. M. Groszek and M. Mytilinaios [1] showed that P− + IΣ2 is sufficient to prove the existence of a high incomplete r.e. set. On the other hand, M. Mytilinaios and T. Slaman [6] showed that P− + IΣ1 is too weak to prove the existence of such a set. A natural question to ask is if the existence of such a set implies IΣ2. In this paper, we will show the answer is negative by constructing a model of P− + IΣ1 + ¬BΣ2 which has a high incomplete r.e. set. Notice that, as shown by M. Groszek and T. Slaman in [2], P− + IΣ1 is too weak to show the transitivity of weak Turing reducibility on Σ2-sets.

The collection of branches (maximal linearly ordered sets of nodes) of the tree <ωω (ordered by inclusion) forms an almost disjoint family (of sets of nodes). This family is not maximal — for example, any level of the tree is almost disjoint from all of the branches. How many sets must be added to the family of branches to make it maximal? This question leads to a series of definitions and results: a set of nodes is off-branch if it is almost disjoint from every branch in the tree; an off-branch family is an almost disjoint family of off-branch sets; and is the minimum cardinality of a maximal off-branch family.

Results concerning include: (in ZFC) , and (consistent with ZFC) is not equal to any of the standard small cardinal invariants or = 2ω. Most of these consistency results use standard forcing notions—for example, in the Cohen model.

Many interesting open questions remain, though—for example, whether .

I will formulate in this paper three set-theoretic axioms, (A1), (A2), and (A3), which appear natural and settle some well-known questions, and I will give some metamathematical evidence supporting these axioms. I build upon a distinction between pure mathematics and applied metamathematics which views the first as an art dealing with imaginary objects, where following Poincaré we can say to exist is to be free of contradiction, and the second as a science describing the phenomenon of mathematics, where science means a description of some physical reality (in this case the reality of thoughts in our brains which underlie spoken or written mathematics). Of course this distinction is not new, but it has been disregarded by many mathematicians and philosophers who wrote about the nature of mathematics, e.g. by the Platonists, and even by some empiricists who thought that mathematics is a science. Since applied metamathematics is a science, unlike pure mathematics it has to be lean, i.e., to obey Ockham's principle of economy of concepts (entia non sunt multiplicanda praeter necessitatem).

In this lean metamathematics we describe pure mathematics as a finite structure of thoughts in our brains, and we think that written or spoken mathematics is an abstract description of this structure. (I think that this is the view which Poincaré expressed informally in his discussions with the logicians and set theorists of his times, although his idea has to be modified to some extent; see Remark 4 at the end of this paper.) We claim that all mathematical objects which are imagined when we develop a (first-order) theory T can be represented by means of terms of the language of a Skolemization of the set of sentences consisting of the axioms of T and of all theorems of logic.