Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-24T20:01:53.099Z Has data issue: false hasContentIssue false
  • English
  • Français

A solution to the completeness problem for weakly aggregative modal logic

Published online by Cambridge University Press:  12 March 2014

Peter Apostoli  and
Bryson Brown
Peter Apostoli
Affiliation:
Department of Philosophy, University of Toronto, Toronto, Ontario, Canada, E-mail: [email protected]
Bryson Brown
Affiliation:
Department of Philosophy, University of Lethbridge, Lethbridge, Alberta, Canada, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

We are accustomed to regarding K as the weakest modal logic admitting of a relational semantics in the style made popular by Kripke. However, in a series of papers which demonstrates a startling connection between modal logic and the theory of paraconsistent inference, Ray Jennings and Peter Schotch have developed a generalized relational frame theory which articulates an infinite hierarchy of sublogics of K, each expressing a species of “weakly aggregative necessity”. Recall that K is axiomatized, in the presence of N and RM, by the schema of “binary aggregation”

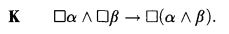
For each n ≥ 1, the weakly aggregative modal logic Kn is axiomatized by replacing K with the schema of “n-ary aggregation”

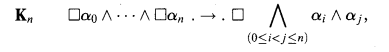
which is an n-ary relaxation, or weakening, of K. Note that K1 = K.

In [3], the authors claim without proof that Kn is determined by the class of frames F = (W, R), where W is a nonempty set and R is an (n + 1)-ary relation on W, under the generalization of Kriple's truth condition according to which □α is true at a point w in W if and only if α is true at one of x1,…,xn for all x1,…, xn in W such that Rw, x1,…, xn.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 60 , Issue 3 , September 1995 , pp. 832 - 842
Copyright
Copyright © Association for Symbolic Logic 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Chellas, Brian L., Modal logic: an introduction, Cambridge University Press, Cambridge, 1980.CrossRefGoogle Scholar
[2]Goldblatt, R. I., Logics of time and computation, CSLI Lecture Notes, No. 7, Center for the Study of Language and Information, Stanford University, Stanford, California, 1978.Google Scholar
[3]Jennings, R. E. and Schotch, P. K., The preservation of coherence, Studia Logica, vol. 43 (1984), pp. 89–106.CrossRefGoogle Scholar
[4]Jennings, R. E. and Schotch, P. K., Some remakrs on (weakly) weak modal logics, Notre Dame Journal of Formal Logic, vol. 22 (1981), pp. 309–314.CrossRefGoogle Scholar
[5]Jennings, R. E., Schotch, P. K., and Johnston, D. K., The n-adic first order undefinahility of the Geach formula, Notre Dame Journal of Formal Logic, vol. 22 (1981), pp. 375–378.CrossRefGoogle Scholar
[6]Jennings, R. E., Schotch, P. K., and Johnston, D. K., Universal first order definability in modal logic, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 26 (1980), pp. 327–330.CrossRefGoogle Scholar
[7]Johnston, D. K., A generalized relational semantics for modal logic, M. A. Thesis, Department of Philosophy, Simon Fraser University, Barnaby, British Columbia, 1978.Google Scholar
[8]Schotch, P. K. and Jennings, R., Inference and necessity, Journal of Philosophical Logic, vol. 9 (1980), pp. 327–340.CrossRefGoogle Scholar
[9]Schotch, P. K. and Jennings, R., Modal logic and the theory of modal aggregation, Philosophia, vol. 9 (1980), pp. 265–278.CrossRefGoogle Scholar
[10]Schotch, P. K. and Jennings, R., On detonating, Paraconsistent logic (Priest, G. and Routley, R., editors), Philosophia Verlag, Munich, 1989, pp. 306–327.CrossRefGoogle Scholar