Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T13:27:21.226Z Has data issue: false hasContentIssue false
  • English
  • Français

A reflection principle and its applications to nonstandard models

Published online by Cambridge University Press:  12 March 2014

James H. Schmerl
James H. Schmerl*
Affiliation:
Department of Mathematics, University Of Connecticut, Storrs, Connecticut 06269-3009, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

Some methods of constructing nonstandard models work only for particular theories, such as ZFC, or CA + AC (which is second order number theory with the choice scheme). The examples of this which motivated the results of this paper occur in the main theorems of [5], which state that if T is any consistent extension of either ZFC0 (which is ZFC but with only countable replacement) or CA + AC and if κ and λ are suitably chosen cardinals, then T has a model which is κ-saturated and has the λ-Bolzano-Weierstrass property. (Compare with Theorem 3.5.) Another example is a result from [12] which states that if T is any consistent extension of CA + AC and cf (λ) > ℵ0, then T has a natural λ-Archimedean model. (Compare with Theorem 3.1 and the comments following it.) Still another example is a result in [6] in which it is shown that if a model 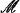of Peano arithmetic is expandable to a model of ZF or of CA, then so is any cofinal extension of 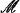. (Compare with Theorem 3.10.) Related types of constructions can also be found in [10] and [11].

A reflection principle will be proved here, allowing these constructions to be extended to models of many other theories, among which are some exceedingly weak theories and also all of their completions.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 60 , Issue 4 , December 1995 , pp. 1137 - 1152
Copyright
Copyright © Association for Symbolic Logic 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Beller, A. and Litman, A., A strengthening of Jensen's □ principles, this Journal, vol. 45 (1980), pp. 251–264.Google Scholar
[2]Chang, C. C. and Keisler, H. J., Model theory, 3rd ed., North-Holland, Amsterdam, 1990.Google Scholar
[3]Devlin, K. J., The combinatorial principle ◊*, this Journal, vol. 47 (1982), pp. 888–899.Google Scholar
[4]Hajnal, A., Kanamori, A., and Shelah, S., Regressive partition relations for infinite cardinals, Transactions of the American Mathematical Society, vol. 299 (1987), pp. 145–154.CrossRefGoogle Scholar
[5]Keisler, H. J. and Schmerl, J., Making the hyperreal line both saturated and complete, this Journal, vol. 56 (1991), pp. 1016–1025.Google Scholar
[6]Kotlarski, H., On cofinal extensions of models of arithmetic, this Journal, vol. 48 (1983), pp. 253–262.Google Scholar
[7]Schmerl, J. H., Peano models with many generic classes, Pacific Journal of Mathematics, vol. 46 (1973), pp. 523–536.CrossRefGoogle Scholar
[7a]Schmerl, J. H., Correction to "Peano models with many generic classes", Pacific Journal of Mathematics, vol. 92 (1981), pp. 195–198.CrossRefGoogle Scholar
[8]Schmerl, J. H., A partition property characterizing cardinals hyperinaccessible of finite type, Transactions of the American Mathematical Society, vol. 188 (1974), pp. 281–291.CrossRefGoogle Scholar
[9]Schmerl, J. H., Generalizing special Aronszajn trees, this Journal, vol. 39 (1974), pp. 732–740.Google Scholar
[10]Schmerl, J. H., Recursively saturated, rather classless models of Peano arithmetic, Logic year 1979–1980 (Lerman, M., editor), Lecture Notes in Mathematics, vol. 859, Springer-Verlag, Berlin, 1981, pp. 268–282.CrossRefGoogle Scholar
[11]Schmerl, J. H., Models of Peano arithmetic and a question of Sikorski on ordered fields, Israel Journal of Mathematics, vol. 50 (1985), pp. 145–159.CrossRefGoogle Scholar
[12]Schmerl, J. H., Peano arithmetic and hyper-Ramsey logic, Transactions of the American Mathematical Society, vol. 296 (1986), pp. 481–505.CrossRefGoogle Scholar
[13]Velleman, D. J., Morasses, diamond, and forcing, Annals of Mathematical Logic, vol. 23 (1982), pp. 199–281.CrossRefGoogle Scholar