Defining multiplication in o-minimal expansions of the additive reals

Extract

This paper considers o-minimal expansions of the structure 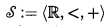—the ordered additive reals. More particularly we consider the case when the expansions are “eventually nonlinear” (see below), and find that multiplication is actually definable in all cases except when the structure is “eventually almost linear”, which is a rare special case in which multiplication is obviously not definable. Thus the main theorem established is:

Theorem 1.1. For 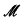an o-minimal expansion o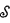f , if 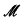is eventually non-almost-linear then multiplication is definable in.

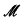(A structure is eventually almost linear iff every definable function f is of the form f(x) = λx + c + ε(x) on some interval (K, ∞), where λ, c Є ℝ and ε is a function of x which tends to 0 faster than any negative power of x as x → +∞. Otherwise, i.e. if there is a definable function which is not of this form, it is eventually non-almost-linear.)

This is proved in §4.1, after §§2 and 3 have established technology concerning the rate of growth of functions and approximating derivatives.

In §4.2 an analogy is made with the result of exponentiation being definable in a polynomially unbounded o-minimal expansion of ℝ as an ordered field (see [Mi]). In fact, by means of the isomorphism x ↦ ln(x) we see that Theorem 1.1 also implies this latter result.

Unless otherwise stated, all structures considered in the paper have ℝ as their universe and all functions are real functions.