This note is written in reply to López-Escobar's paper [L-E] where a “sequence” of intermediate propositional systems NLCn (n ≥ 1) and corresponding implicative propositional systems NLICn (n ≥ 1) is given. We will show that the “sequence” NLCn contains three different systems only. These are the classical propositional calculus NLC1, Dummett's system NLC2 and the system NLC3. Accordingly (see [C], [Hs2], [Hs3], [B 1], [B2], [Hs4], [L-E]), the problem posed in the paper [L-E] can be formulated as follows: is NLC3a conservative extension of NLIC3? Having in mind investigations of intermediate propositional calculi that give more general results of this type (see V. I. Homič [H1], [H2], C. G. McKay [Mc], T. Hosoi [Hs 1]), in this note, using a result of Homič (Theorem 2, [H1]), we will give a positive solution to this problem.

NLICnand NLCn. If X and Y are propositional logical systems, by X ⊆ Y we mean that the set of all provable formulas of X is included in that of Y. And X = Y means that X ⊆ Y and Y ⊆ X. A(P1/B1, …, Pn/Bn) is the formula (or the sequent) obtained from the formula (or the sequent) A by substituting simultaneously B1, …, Bn for the distinct propositional variables P1, …, Pn in A.

Let Cn(n ≥ 1) be the string of the following sequents:

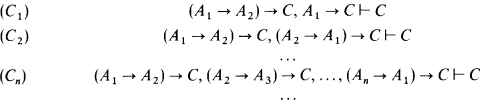
Having in mind that the calculi of sequents can be understood as meta-calculi for the deducibility relation in the corresponding systems of natural deduction (see [P]), the systems of natural deductions NLCn and NLICn (n ≥ 1), introduced in [L-E], can be identified with the calculi of sequents obtained by adding the sequents Cn as axioms to a sequential formulation of the Heyting propositional calculus and to a system of positive implication, respectively (see [C], [Ch], [K], [P]).

This work results from an attempt to give the vague notion of relevance a concrete semantical interpretation. The idea is that propositions may be divided into different “domains of relevance”. Each “domain” has its own “T” and “F” values, and propositions “belonging” to one domain can never entail propositions “belonging” to another, unconnected one.

The semantics we have developed were found to correspond to an already known system, which we call here RMI⥲. Its axioms are the implication-negation axioms of the system RM ([1, Chapter 5]). However, as Meyer has shown, RM is not a conservative extension of RMI⥲, since RMI⥲ has the sharing-of-variables property ([5], and [1, pp. 148–149[), which the implication-negation fragment of RM has not.

RMI⥲ has four advantages in comparison to its more famous sister R⥲ (the pure intentional fragment of the system R; see [1]):

a) It has a very natural (from a relevance point of view) many-valued semantics, the simple form of which we describe here.

b) RMI⥲, ⊢ A1 → [A2 → (… → (An → A) …)] iff there is a proof of A from the set {A1, …, An} that actually uses all the members of this set. In R⥲, this holds only if we talk about “sequences” instead of “sets”. This is somewhat less intuitive (see [1, pp. 394–395]).

c) RMI⥲ is a maximal “natural” relevance logic, in the sense that every proper extension of it limits the number of “domains of relevance” (§III).

Abstract.

Banach introduced the following two-person, perfect information, infinite game on the real numbers and asked the question: For which sets A ⊆ R is the game determined?

Rules: The two players alternate moves starting with player I. Each move an is legal iff it is a real number and 0 < an, and for n > 1, an < an−1. The first player to make an illegal move loses. Otherwise all moves are legal and I wins iff exists and .

We will look at this game and some variations of it, called Banach games. In each case we attempt to find the relationship between Banach determinacy and the determinacy of other well-known and much-studied games.

Solovay has shown that if F: [ω]ω → 2 is a clopen partition with recursive code, then there is an infinite homogeneous hyperarithmetic set for the partition (a basis result). Simpson has shown that for every 0α, where α is a recursive ordinal, there is a clopen partition F: [ω]ω → 2 such that every infinite homogeneous set is Turing above 0α (an anti-basis result). Here we refine these results, by associating the “order type” of a clopen set with the Turing complexity of the infinite homogeneous sets. We also consider the Nash-Williams barrier theorem and its relation to the clopen Ramsey theorem.

In this note it is shown that the property of orthomodularity of the lattice of orthoclosed subspaces of a pre-Hilbert space is not determined by any first-order properties of the relation ⊥ of orthogonality between vectors in . Implications for the study of quantum logic are discussed at the end of the paper.

The key to this result is the following:

Ifis a separable Hilbert space, andis an infinite-dimensional pre-Hilbert subspace of, then (, ⊥) and (, ⊥) are elementarily equivalent in the first-order languageL2of a single binary relation.

Choosing to be a pre-Hilbert space whose lattice of orthoclosed subspaces is not orthomodular, we obtain our desired conclusion. In this regard we may note the demonstration by Amemiya and Araki [1] that orthomodularity of the lattice of orthoclosed subspaces is necessary and sufficient for a pre-Hilbert space to be metrically complete, and hence be a Hilbert space. Metric completeness being a notoriously nonelementary property, our result is only to be expected (note also the parallel with the elementary L2-equivalence of the natural order (Q, <) of the rationals and its metric completion to the reals (R, <)).

To derive (1), something stronger is proved, viz. that (, ⊥) is an elementary substructure of (, ⊥).

Un espace ultramétrique est un ensemble muni d'une distance à valeurs dans un ordre total avec premier élément et pour laquelle tout triangle est isocèle avex deux grands côtés égaux. Les deux cas importants d'espaces ultramétriques sont:

(1) les corps valués lorsqu'on ne considère que leur structure métrique, et

(2) les ensembles Aλ, où λ est un ensemble bien ordonné, munis de la distance d(α, β) = inf {γ ∈ λ; α(γ) ≠ β(γ)} si α ≠ β et d(α, β) = 0 sinon; distance à valeurs dans l'ordre inverse de λ enrichi d'un premier élément 0.

Nous étudions ces structures dans un langage comportant un seul type de variables, les points de l'espace, et un prédicat à quatre places traduisant l'ordre sur les distances

Nous définissons la notion d'espace riche, qui est la modèle-complétion relative à un ensemble des distances fixé: un espace est riche si et seulement s'il est existentiellement clos dans toute extension qui n'ajoute pas de nouvelle distance. Les deux exemples précédemment donnés, espaces Aλ et corps valués, fournissent des espaces riches. La suite de l'article s'attache à la description des espaces riches.

Let PA be the theory of first order Peano arithmetic, in the language L with binary operation symbols + and ·. Let N be the theory of the standard model of PA. We consider countable models M of PA such that the universe ∣M∣ is ω. The degree of such a model M, denoted by deg(M), is the (Turing) degree of the atomic diagram of M. The results of this paper concern the degrees of models of N, but here in the Introduction, we shall give a brief survey of results about degrees of models of PA.

Let D0 denote the set of degrees d such that there is a nonstandard model of M of PA with deg(M) = d. Here are some of the more easily stated results about D0.

(1) There is no recursive nonstandard model of PA; i.e., 0 ∈ D0.

This is a result of Tennenbaum [T].

(2) There existsd ∈ D0such thatd ≤ 0′.

This follows from the standard Henkin argument.

(3) There existsd ∈ D0such thatd < 0′.

Shoenfield [Sh1] proved this, using the Kreisel-Shoenfield basis theorem.

(4) There existsd ∈ D0such thatd′ = 0′.

Jockusch and Soare [JS] improved the Kreisel-Shoenfield basis theorem and obtained (4).

(5) D0 = Dc = De, where Dc denotes the set of degrees of completions of PA and De the set of degrees d such that d separates a pair of effectively inseparable r.e. sets.

Solovay noted (5) in a letter to Soare in which in answer to a question posed in [JS] he showed that Dc is upward closed.

The question of the limits of recursive enumerability was first formulated by Sacks (1980) and investigated further in Sacks (198?). E-recursion or “set recursion”, as a natural generalization of Kleene recursion in normal objects of finite type, was introduced by Normann (1978) in order to facilitate the study of the degrees of functionals. We shall extend the work of Sacks on the question of how definable is the E-closure of an ordinal α (written E(α)). We write gc(κ) to denote the largest τ < κ such that Lκ ⊨ “τ is a cardinal” and cf (τ) for τ ∈ ON to denote the cofinality of τ.

In §1 we give the basic definitions and state the results of Silver and Friedman (1980) used by Sacks to show that if E(α) = Lκ and is not Σ1-admissible and

then P(gc(κ)) ∩ Lκ is indexical on Lκ and hence RE. We show in this case first that P(gc(κ)) ∩ Lκ indexical implies that Lκ is indexical (and hence RE).

In §2 we introduce the notion of a “nonstandard stage comparison” and use it to extend the definability result of §1 to show that this Lκ is in fact REC. Finally we remark that E(α) is indexical if and only if E(α) is RE.

The importance of the logical ‘generalized quantifiers’ (Mostowski [1957]) for the semantics of natural language was brought out clearly in Barwise & Cooper [1981]. Basically, the idea is that a quantifier phrase QA (such as “all women”, “most children”, “no men”) refers to a set of sets of individuals, viz. those B for which (QA)B holds. Thus, e.g., given a fixed model with universe E,

where ⟦A⟧ is the set of individuals forming the extension of the predicate “A” in the model. This point of view permits an elegant and uniform semantic treatment of the subject-predicate form that pervades natural language.

Such denotations of quantifier phrases exhibit familiar mathematical structures. Thus, for instance, all A produces filters, and no A produces ideals. The denotation of most A is neither; but it is still monotone, in the sense of being closed under supersets. Mere closure under subsets occurs too; witness a quantifier phrase like few A. These mathematical structures are at present being used in organizing linguistic observations and formulating hypotheses about them. In addition to the already mentioned paper of Barwise & Cooper, an interesting example is Zwarts [1981], containing applications to the phenomena of “negative polarity” and “conjunction reduction”. In the course of the latter investigation, several methodological issues of a wider logical interest arose, and these have inspired the present paper.

In order to present these issues, let us shift the above perspective, placing the emphasis on quantifier expressions per se (“all”, “most”, “no”, “some”, etcetera), viewed as denoting relations Q between sets of individuals.

We exhibit a Horn sentence expressing the statement of the title; the construction generalizes to arbitrary primes in place of five.

We prove that every relation-universal model of an ω-stable theory is saturated. We also show there is a large class of ω-stable theories for which every resplendent model is homogeneous.

A first order representation (f.o.r.) in topology is an assignment of finitary relational structures of the same type to topological spaces in such a way that homeomorphic spaces get sent to isomorphic structures. We first define the notions “one f.o.r. is at least as expressive as another relative to a class of spaces” and “one class of spaces is definable in another relative to an f.o.r.”, and prove some general statements. Following this we compare some well-known classes of spaces and first order representations. A principal result is that if X and Y are two Tichonov spaces whose posets of zero-sets are elementarily equivalent then their respective rings of bounded continuous real-valued functions satisfy the same positive-universal sentences. The proof of this uses the technique of constructing ultraproducts as direct limits of products in a category theoretic setting.

An important problem, widely treated in the analysis of the structure of degree orderings, is that of partial order and lattice embeddings. Thus for example we have the results on embeddings of all countable partial orderings in the Turing degrees by Kleene and Post [3] and in the r.e. T-degrees by Sacks [10]. For lattice embeddings the work on T-degrees culminated in the characterization of countable initial segments by Lachlan and Lebeuf [4]. For the r.e. T-degrees there has been a continuing line of progress on this question. (See Soare [20] and Lerman, Shore, and Soare [8].) Similar projects have been undertaken for the T-degrees below 0′ (Kleene and Post [3], Lerman [6]) as well as for most other degree orderings. The results have been used not only to analyse individual orderings but also to distinguish between them (Shore [16], [19], [17]).

The situation for α-jecursive theory, the study of recursion in (admissible) ordinals, is similar to, though not as well developed as, that for Turing degrees. All afinite partial orderings have been embedded even in the α-r.e. degrees (see Lerman [5]). Lattice embedding results are somewhat fragmentary however. In terms of initial segments even the question of the existence of a minimal α-degree has not been settled for all admissibles. (See Shore [12] for a proof for Σ2-admissible ordinals, however.) Results on more complicated lattices have only reached to the finite distributive ones for Σ3-admissible ordinals (see Dorer [1]).

As in Rogers [3], we treat the partial degrees as notational variants of the enumeration degrees (that is, the partial degree of a function is identified with the enumeration degree of its graph). We showed in [1] that there are no minimal partial degrees. The purpose of this paper is to show that the partial degrees below 0′ (that is, the partial degrees of the Σ2 partial functions) are dense. From this we see that the Σ2 sets play an analagous role within the enumeration degrees to that played by the recursively enumerable sets within the Turing degrees. The techniques, of course, are very different to those required to prove the Sacks Density Theorem (see [4, p. 20]) for the recursively enumerable Turing degrees.

Notation and terminology are similar to those of [1]. In particular, We, Dx, 〈m, n〉, ψe are, respectively, notations for the e th r.e. set in a given standard listing of the r.e. sets, the finite set whose canonical index is x, the recursive code for (m, n) and the e th enumeration operator (derived from We). Recursive approximations etc. are also defined as in [1].

Theorem 1. If B and C are Σ2sets of numbers, and B ≰e C, then there is an e-operator Θ with

Proof. We enumerate an e-operator Θ so as to satisfy the list of conditions:

Let {Bs ∣ s ≥ 0}, {Cs ∣ s ≥ 0} be recursive sequences of approximations to B, C respectively, for which, for each х, х ∈ B ⇔ (∃s*)(∀s ≥ s*)(х ∈ Bs) and х ∈ C ⇔ (∃s*)(∀s ≥ s*)(х ∈ Cs).

This paper deals with locales and their spaces of points in intuitionistic analysis or, if you like, in (Grothendieck) toposes. One of the important aspects of the problem whether a certain locale has enough points is that it is directly related to the (constructive) completeness of a geometric theory. A useful exposition of this relationship may be found in [1], and we will assume that the reader is familiar with the general framework described in that paper.

We will consider four formal spaces, or locales, namely formal Cantor space C, formal Baire space B, the formal real line R, and the formal function space RR being the exponential in the category of locales (cf. [3]). The corresponding spaces of points will be denoted by pt(C), pt(B), pt(R) and pt(RR). Classically, these locales all have enough points, of course, but constructively or in sheaves this may fail in each case. Let us recall some facts from [1]: the assertion that C has enough points is equivalent to the compactness of the space of points pt(C), and is traditionally known in intuitionistic analysis as the Fan Theorem (FT). Similarly, the assertion that B has enough points is equivalent to the principle of (monotone) Bar Induction (BI). The locale R has enough points iff its space of points pt(R) is locally compact, i.e. the unit interval pt[0, 1] ⊂ pt(R) is compact, which is of course known as the Heine-Borel Theorem (HB). The statement that RR has enough points, i.e. that there are “enough” continuous functions from R to itself, does not have a well-established name. We will refer to it (not very imaginatively, I admit) as the principle (EF) of Enough Functions.

The most common way of proving decidability in propositional modal logic is to shew that the system in question has the finite model property. This is not however the only way. Gabbay in [4] proves the decidability of many modal systems using Rabin's result in [8] on the decidability of the second-order theory of successor functions. In particular [4, pp. 258-265] he is able to prove the decidability of a system which lacks the finite model property. Gabbay's system is however complete, in the sense of being characterized by a class of frames, and the question arises whether there is a decidable modal logic which is not complete. Since no incomplete modal logic has the finite model property [9, p. 33], any proof of decidability must employ some such method as Gabbay's. In this paper I use the Gabbay/Rabin technique to prove the decidability of a finitely axiomatized normal modal propositional logic which is not characterized by any class of frames. I am grateful to the referee for suggesting improvements in substance and presentation.

The terminology I am using is standard in modal logic. By a frame is understood a pair 〈W, R〉 in which W is a class (of “possible worlds”) and R ⊆ W2. To avoid confusion in what follows, a frame will henceforth be referred to as a Kripke frame. By contrast, a general frame is a pair 〈, Π〉 in which is a Kripke frame and Π is a collection of subsets of W closed under the Boolean operations and satisfying the condition that if A is in Π then so is R−1 “A. A model on a frame (of either kind) is obtained by adding a function V which assigns sets of worlds to propositional variables. In the case of a general frame we require that V(p) ∈ Π.

We examine the multiplicity of complementation amongst subspaces of V∞. A subspace V is a complement of a subspace W if V ∩ W = {0} and (V ∪ W)* = V∞. A subspace is called fully co-r.e. if it is generated by a co-r.e. subset of a recursive basis of V∞. We observe that every r.e. subspace has a fully co-r.e. complement.

Theorem. If S is any fully co-r.e. subspace then S has a decidable complement.

We give an analysis of other types of complements S may have. For example, if S is fully co-r.e. and nonrecursive, then S has a (nonrecursive) r.e. nowhere simple complement.

We impose the condition of immunity upon our subspaces.

Theorem. Suppose V is fully co-r.e. Then V is immune iff there exist M1, M2 ∈ L(V∞), with M1supermaximal and M2k-thin, such that M1, ⊕ V = M2 ⊕ V = V∞.

Corollary. Suppose V is any r.e. subspace with a fully co-r.e. immune complement W(e.g., V is maximal or V is h-immune). Then there exist an r.e. supermaximal subspace M and a decidable subspace D such that V ⊕ W = M ⊕ W = D ⊕ W = V∞.

We indicate how one may obtain many further results of this type. Finally we examine a generalization of the concepts of immunity and soundness. A subspace V of V∞ is nowhere sound if (i) for all Q ∈ L(V∞) if Q ⊃ V then Q = V∞, (ii) V is immune and (iii) every complement of V is immune. We analyse the existence (and ramifications of the existence) of nowhere sound spaces.

Let λ be an ordinal less than or equal to an infinite cardinal κ. For S ⊂ κ, [S]λ denotes the collection of all order type λ subsets of S. A set X ⊂ [κ]λ will be called Ramsey iff there exists p ∈ [κ]κ such that either [p]λ ⊂ X or [p]λ ∩ X = ∅. The set p is called homogeneous for X.

The infinite Ramsey theorem implies that all subsets of [ω]n are Ramsey for n < ω. Using the axiom of choice, one can define a non-Ramsey subset of [ω]ω. In [GP], Galvin and Prikry showed that all Borel subsets of [ω]ω are Ramsey, where one topologizes [ω]ω as a subspace of Baire space. Silver [S] proved that analytic sets are Ramsey, and observed that this is best possible in ZFC.

When κ > ω, the assertion that all subsets of [κ]n are Ramsey is a large cardinal hypothesis equivalent to κ being weakly compact (and strongly inaccessible). Again, is not possible in ZFC to have all subsets of [κ]ω Ramsey. The analogy to the Galvin-Prikry theorem mentioned above was established by Kleinberg, extending work by Kleinberg and Shore in [KS]. The set [κ]ω is given a topology as a subspace of κω, which has the usual product topology, κ taken as discrete. It was shown that all open subsets of [κ]ω are Ramsey iff κ is a Ramsey cardinal (that is, κ → (κ)<ω).

In this note we examine the spaces [κ]λ for κ ≥ λ ≥ ω. We show that κ Ramsey implies all open subsets of [κ]λ are Ramsey for λ < κ, and that if κ is measurable, then all open subsets of [κ]κ are Ramsey. Let us remark here that we can with the same methods prove these results with “κ-Borel” in the place of “open”, where the κ-Borel sets are the smallest collection containing the opens and closed under complementation and intersections of length less than κ. Also, although here we consider just subsets of [κ]λ, it is no more difficult to show that partitions of [κ]λ into less than κ many κ-Borel sets have, under the appropriate hypothesis, size κ homogeneous sets.

Forcing with [Κ]κ over a model of set theory with a strong partition cardinal, M. Spector produced a generic ultrafilter G on κ such that κκ/G is not well-founded.

Theorem. Let G be Spector-generic over a model M of , for all α < κ.

1) Every cardinal (well-ordered or not) of M is a cardinal of M[G].

2) If A ∈ M[G] is a well-ordered subset of M, then Ae M. Let Φ = Κκ/G.

3) There is an ultrafilter U on Φ such that every member of U has a subset of type Φ, and the intersection of any well-ordered subset of U is in U.

4) Φ satisfies for all α <ℵ1 and all ordinals β.

5) There is a linear order Φ′ with property 3) above which is not “weakly compact”, i.e., Φ′ ↛ (Φ′)2.

In a series of papers [K2], [K3], [K4], E. M. Kleinberg established the extensive properties of what are now called “strong partition cardinals”, cardinals satisfying for all λ < κ. The purpose of this note is to show that all these consequences and the results in [H] and [W] can be obtained from the weaker relation and many from .

We assume the reader is generally familiar with Kleinberg's machinery and with the definition of . We recall that a cardinal κ satisfies iff for every partition F: [κ]κ → A there is a p ∈ [κ]κ such that F″ [p]κ ≠ A. We take the liberty of regarding a p ∈ [κ]κ both as a subset of κ and as a function from κ to κ. We assume DC throughout.

§1. From. Our results stem from the observation that the proofs in the papers cited above only require homogeneous sets for certain classes of partitions.

Definition. A partition F: [κ]κ → λ, λ < λ, is called clopen if for all p ∈ [κ]κ there is an α < κ such that whenever -clopen is the assertion that all clopen partitions have homogeneous sets (Spector-Watro).