Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-29T01:59:12.218Z Has data issue: false hasContentIssue false
  • English
  • Français

Banach games

Published online by Cambridge University Press:  12 March 2014

Chris Freiling
Chris Freiling*
Affiliation:
University of California, Santa Barbara, California 93106
Get access Rights & Permissions [Opens in a new window]

Abstract

Abstract.

Banach introduced the following two-person, perfect information, infinite game on the real numbers and asked the question: For which sets A ⊆ R is the game determined?

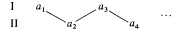
Rules: The two players alternate moves starting with player I. Each move an is legal iff it is a real number and 0 < an, and for n > 1, an < an−1. The first player to make an illegal move loses. Otherwise all moves are legal and I wins iff 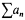exists and .

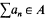We will look at this game and some variations of it, called Banach games. In each case we attempt to find the relationship between Banach determinacy and the determinacy of other well-known and much-studied games.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 49 , Issue 2 , June 1984 , pp. 343 - 375
Copyright
Copyright © Association for Symbolic Logic 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Davis, M. [1964], Infinite games of perfect information, Advances in game theory, Annals of Mathematics Studies, vol. 52, Princeton University Press, Princeton, New Jersey, pp. 85–101.Google Scholar
Gale, D. and Stewart, F. M. [1953], Infinite games with perfect information, Contributions to the theory of games, vol. 2, Annals of Mathematics Studies, vol. 28, Princeton University Press, Princeton, New Jersey, pp. 245–266.Google Scholar
Martin, D. A. [1975], Borel determinacy, Annals of Mathematics, ser. 2, vol. 102, pp. 363–371.CrossRefGoogle Scholar
Moschovakis, Y. N. [1980], Descriptive set theory, North-Holland, Amsterdam.Google Scholar
Mycielski, J. [1964], On the axiom of determinateness, Fundamenta Mathematicae, vol. 53, pp. 205–224.CrossRefGoogle Scholar
Mycielski, J. [1966], On the axiom of determinateness. II, Fundamenta Mathematicae, vol. 59, pp. 203–212.CrossRefGoogle Scholar
Mycielski, J. and Steinhaus, H. [1962], A mathematical axiom contradicting the axiom of choice, Bulletin de l'Académie Polonaise des Sciences. Séries des Sciences Mathématiques, Astronomiques et Physiques, vol. 10, pp. 1–3.Google Scholar
Mycielski, J. and Świerczkowski, S. [1964], On the Lebesgue measurability and the axiom of determinateness, Fundamenta Mathematicae, vol. 54, pp. 67–71.CrossRefGoogle Scholar
Oxtoby, J. C. [1957], The Banach-Mazur game and Banach category theorem, Contributions to the theory of games, vol. 3, Annals of Mathematics Studies, vol. 39, Princeton University Press, Princeton, N.J., pp. 159–163.Google Scholar
Schmidt, W. M. [1980], Diophantine approximation, Springer-Verlag, Berlin.Google Scholar
Ulam, S. M. [1977], The Scottish book, Los Alamos Scientific Laboratory of the University of California, Los Alamos, New Mexico.Google Scholar