Published online by Cambridge University Press: 12 March 2014
As in Rogers [3], we treat the partial degrees as notational variants of the enumeration degrees (that is, the partial degree of a function is identified with the enumeration degree of its graph). We showed in [1] that there are no minimal partial degrees. The purpose of this paper is to show that the partial degrees below 0′ (that is, the partial degrees of the Σ2 partial functions) are dense. From this we see that the Σ2 sets play an analagous role within the enumeration degrees to that played by the recursively enumerable sets within the Turing degrees. The techniques, of course, are very different to those required to prove the Sacks Density Theorem (see [4, p. 20]) for the recursively enumerable Turing degrees.
Notation and terminology are similar to those of [1]. In particular, We, Dx, 〈m, n〉, ψe are, respectively, notations for the e th r.e. set in a given standard listing of the r.e. sets, the finite set whose canonical index is x, the recursive code for (m, n) and the e th enumeration operator (derived from We). Recursive approximations 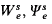 etc. are also defined as in [1].
etc. are also defined as in [1].
Theorem 1. If B and C are Σ2sets of numbers, and B ≰e C, then there is an e-operator Θ with
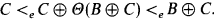
Proof. We enumerate an e-operator Θ so as to satisfy the list of conditions:
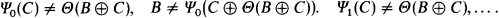
Let {Bs ∣ s ≥ 0}, {Cs ∣ s ≥ 0} be recursive sequences of approximations to B, C respectively, for which, for each х, х ∈ B ⇔ (∃s*)(∀s ≥ s*)(х ∈ Bs) and х ∈ C ⇔ (∃s*)(∀s ≥ s*)(х ∈ Cs).