No CrossRef data available.
Article contents
The definability of E(α)
Published online by Cambridge University Press: 12 March 2014
Extract
The question of the limits of recursive enumerability was first formulated by Sacks (1980) and investigated further in Sacks (198?). E-recursion or “set recursion”, as a natural generalization of Kleene recursion in normal objects of finite type, was introduced by Normann (1978) in order to facilitate the study of the degrees of functionals. We shall extend the work of Sacks on the question of how definable is the E-closure of an ordinal α (written E(α)). We write gc(κ) to denote the largest τ < κ such that Lκ ⊨ “τ is a cardinal” and cf (τ) for τ ∈ ON to denote the cofinality of τ.
In §1 we give the basic definitions and state the results of Silver and Friedman (1980) used by Sacks to show that if E(α) = Lκ and is not Σ1-admissible and
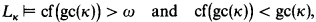
then P(gc(κ)) ∩ Lκ is indexical on Lκ and hence RE. We show in this case first that P(gc(κ)) ∩ Lκ indexical implies that Lκ is indexical (and hence RE).
In §2 we introduce the notion of a “nonstandard stage comparison” and use it to extend the definability result of §1 to show that this Lκ is in fact REC. Finally we remark that E(α) is indexical if and only if E(α) is RE.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1984


