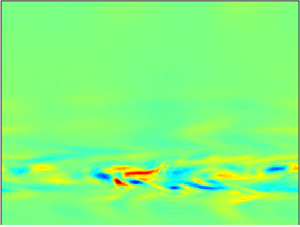
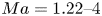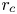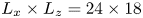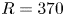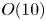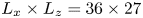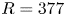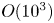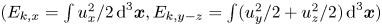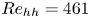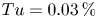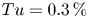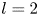Graphical abstract from Doinikov, A., Regnault, G., Mauger, C., Blanc-Benon, P. & Inserra, C. 2022 Acoustic microstreaming produced by two interacting gas bubbles undergoing axisymmetric shape oscillations. J. Fluid Mech. 931, A19. doi:10.1017/jfm.2021.926.
JFM Papers
Swimming of a ludion in a stratified sea
-
- Published online by Cambridge University Press:
- 24 November 2021, A14
-
- Article
- Export citation
Reflectionless wave propagation on shallow water with variable bathymetry and current
-
- Published online by Cambridge University Press:
- 24 November 2021, A15
-
- Article
- Export citation
Experimental investigation of supersonic boundary-layer tripping with a spanwise pulsed spark discharge array
-
- Published online by Cambridge University Press:
- 24 November 2021, A16
-
- Article
- Export citation
On mixing enhancement by secondary baroclinic vorticity in a shock–bubble interaction
-
- Published online by Cambridge University Press:
- 26 November 2021, A17
-
- Article
- Export citation
Asymptotics of streamwise Reynolds stress in wall turbulence
-
- Published online by Cambridge University Press:
- 29 November 2021, A18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Acoustic microstreaming produced by two interacting gas bubbles undergoing axisymmetric shape oscillations
-
- Published online by Cambridge University Press:
- 26 November 2021, A19
-
- Article
- Export citation
Viscous flow around three-dimensional macroscopic cavities in a granular material
-
- Published online by Cambridge University Press:
- 26 November 2021, A20
-
- Article
- Export citation
Turbulent flow in curved channels
-
- Published online by Cambridge University Press:
- 26 November 2021, A21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Collapse of transitional wall turbulence captured using a rare events algorithm
-
- Published online by Cambridge University Press:
- 26 November 2021, A22
-
- Article
- Export citation
Microlayer dynamics during the growth process of a single vapour bubble under subcooled flow boiling conditions
-
- Published online by Cambridge University Press:
- 26 November 2021, A23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Transition in an infinite swept-wing boundary layer subject to surface roughness and free-stream turbulence
-
- Published online by Cambridge University Press:
- 26 November 2021, A24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
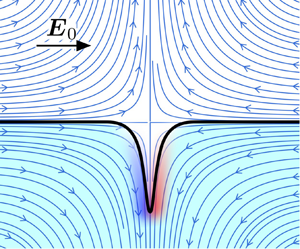
Instability of a planar fluid interface under a tangential electric field in a stagnation point flow
-
- Published online by Cambridge University Press:
- 26 November 2021, A25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Instability of a dusty Kolmogorov flow
-
- Published online by Cambridge University Press:
- 26 November 2021, A26
-
- Article
- Export citation
There is no critical mass ratio for galloping of a square cylinder under flow
-
- Published online by Cambridge University Press:
- 26 November 2021, A27
-
- Article
- Export citation
Approach to the 4/3 law for turbulent pipe and channel flows examined through a reformulated scale-by-scale energy budget
-
- Published online by Cambridge University Press:
- 26 November 2021, A28
-
- Article
- Export citation
Magnetoconvection in a horizontal duct flow at very high Hartmann and Grashof numbers
-
- Published online by Cambridge University Press:
- 26 November 2021, A29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Pressure fluctuations due to ‘trapped waves’ in the initial region of compressible jets
-
- Published online by Cambridge University Press:
- 29 November 2021, A30
-
- Article
- Export citation
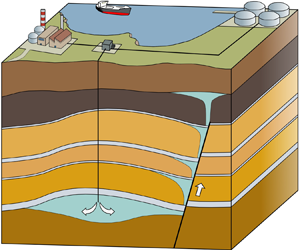
Leakage dynamics of fault zones: experimental and analytical study with application to CO2 storage
-
- Published online by Cambridge University Press:
- 29 November 2021, A31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Analyses of wave-phase variation of Reynolds shear stress underneath surface wave using streamline coordinates
-
- Published online by Cambridge University Press:
- 01 December 2021, A32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Damped shape oscillations of a viscous compound droplet suspended in a viscous host fluid
-
- Published online by Cambridge University Press:
- 01 December 2021, A33
-
- Article
- Export citation