Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-27T20:48:13.191Z Has data issue: false hasContentIssue false
  • English
  • Français

On mixing enhancement by secondary baroclinic vorticity in a shock–bubble interaction

Published online by Cambridge University Press:  26 November 2021

Hong Liu Open the ORCID record for Hong Liu [Opens in a new window] ,
Bin Yu Open the ORCID record for Bin Yu [Opens in a new window] ,
Bin Zhang Open the ORCID record for Bin Zhang [Opens in a new window]  and
Yang Xiang Open the ORCID record for Yang Xiang [Opens in a new window]
Hong Liu*
Affiliation:
School of Aeronautics and Astronautics, Shanghai Jiao Tong University, Shanghai 200240, PR China
Bin Yu*
Affiliation:
School of Aeronautics and Astronautics, Shanghai Jiao Tong University, Shanghai 200240, PR China
Bin Zhang
Affiliation:
School of Aeronautics and Astronautics, Shanghai Jiao Tong University, Shanghai 200240, PR China
Yang Xiang
Affiliation:
School of Aeronautics and Astronautics, Shanghai Jiao Tong University, Shanghai 200240, PR China
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

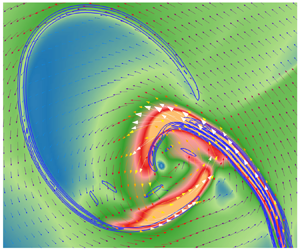
To investigate the intrinsic mechanism for mixing enhancement by variable-density (VD) behaviour, a canonical VD mixing extracted from a supersonic streamwise vortex protocol, a shock–bubble interaction (SBI), is numerically studied and compared with a counterpart of passive-scalar (PS) mixing. It is meaningful to observe that the maximum concentration decays much faster in a VD SBI than in a PS SBI regardless of the shock Mach number ($Ma=1.22 - 4$). The quasi-Lamb–Oseen-type velocity distribution in the PS SBI is found by analysing the azimuthal velocity that stretches the bubble. Meanwhile, for the VD SBI, an additional stretching enhanced by the secondary baroclinic vorticity (SBV) production contributes to the faster-mixing decay. The underlying mechanism of the SBV-enhanced stretching is further revealed through the density and velocity difference between the light shocked bubble and the heavy ambient air. By combining the SBV-accelerated stretching model and the initial shock compression, a novel mixing time estimation for VD SBI is theoretically proposed by solving the advection–diffusion equation under a deformation field of an axisymmetric vortex with the additional SBV-induced azimuthal velocity. Based on the mixing time model, a mixing enhancement number, defined by the ratio of VD and PS mixing time further, reveals the contribution from the VD effect, which implies a better control of the density distribution for mixing enhancement in a supersonic streamwise vortex.

JFM classification

Compressible Flows: Shock waves Flow Control: Mixing enhancement Vortex Flows: Vortex dynamics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 931 , 25 January 2022 , A17
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bagabir, A. & Drikakis, D. 2001 Mach number effects on shock-bubble interaction. Shock Waves 11 (3), 209–218.CrossRefGoogle Scholar
Basu, S., Barber, T.J. & Cetegen, B.M. 2007 Computational study of scalar mixing in the field of a gaseous laminar line vortex. Phys. Fluids 19 (5), 053601.CrossRefGoogle Scholar
Batchelor, G.K. 1959 Small-scale variation of convected quantities like temperature in turbulent fluid. Part 1. General discussion and the case of small conductivity. J. Fluid Mech. 5 (1), 113–133.CrossRefGoogle Scholar
Brouillette, M. 2002 The Richtmyer–Meshkov instability. Annu. Rev. Fluid Mech. 34 (1), 445–468.CrossRefGoogle Scholar
Buch, K.A. & Dahm, W.J.A. 1996 Experimental study of the fine-scale structure of conserved scalar mixing in turbulent shear flows. Part 1. $Sc\gg 1$. J. Fluid Mech. 317, 21–71.CrossRefGoogle Scholar
Cetegen, B.M. & Mohamad, N. 1993 Experiments on liquid mixing and reaction in a vortex. J. Fluid Mech. 249, 391–414.CrossRefGoogle Scholar
Chan, J. 2010 Numerically simulated comparative performance of a scramjet and shcramjet at Mach 11. J. Propul. Power 26 (5), 1125–1134.CrossRefGoogle Scholar
Curran, E.T., Heiser, W.H. & Pratt, D.T. 1996 Fluid phenomena in scramjet combustion systems. Annu. Rev. Fluid Mech. 28 (1), 323–360.CrossRefGoogle Scholar
Dimotakis, P.E. 2005 Turbulent mixing. Annu. Rev. Fluid Mech. 37, 329–356.CrossRefGoogle Scholar
Ding, J., Si, T., Chen, M., Zhai, Z., Lu, X. & Luo, X. 2017 On the interaction of a planar shock with a three-dimensional light gas cylinder. J. Fluid Mech. 828, 289–317.CrossRefGoogle Scholar
Dora, C.L., Murugan, T., De, S. & Das, D. 2014 Role of slipstream instability in formation of counter-rotating vortex rings ahead of a compressible vortex ring. J. Fluid Mech. 753, 29–48.CrossRefGoogle Scholar
Drikakis, D., Hahn, M., Mosedale, A. & Thornber, B. 2009 Large eddy simulation using high-resolution and high–order methods. Phil. Trans. R. Soc. A 367 (1899), 2985–2997.CrossRefGoogle ScholarPubMed
Gharib, M., Rambod, E. & Shariff, K. 1998 A universal time scale for vortex ring formation. J. Fluid Mech. 360, 121–140.CrossRefGoogle Scholar
Giordano, J. & Burtschell, Y. 2006 Richtmyer–Meshkov instability induced by shock-bubble interaction: numerical and analytical studies with experimental validation. Phys. Fluids 18 (3), 036102.CrossRefGoogle Scholar
Glezer, A. 1988 The formation of vortex rings. Phys. Fluids (1958–1988) 31 (12), 3532–3542.CrossRefGoogle Scholar
Gottlieb, S. & Shu, C.-W. 1998 Total variation diminishing Runge–Kutta schemes. Math. Comput. 67 (221), 73–85.CrossRefGoogle Scholar
Groom, M. & Thornber, B. 2021 Reynolds number dependence of turbulence induced by the Richtmyer–Meshkov instability using direct numerical simulations. J. Fluid Mech. 908, A31.CrossRefGoogle Scholar
Gupta, R.N., Yos, J.M. & Thompson, R.A. 1989 A review of reaction rates and thermodynamic and transport properties for the 11-species air model for chemical and thermal nonequilibrium calculations to 30 000 K. NASA STI/Recon Tech. Rep. N 89(6), 32–34.Google Scholar
Gupta, S., Zhang, S. & Zabusky, N.J. 2003 Shock interaction with a heavy gas cylinder: emergence of vortex bilayers and vortex-accelerated baroclinic circulation generation. Laser Part. Beams 21 (03), 443–448.CrossRefGoogle Scholar
Hahn, M., Drikakis, D., Youngs, D.L. & Williams, R.J.R. 2011 Richtmyer–Meshkov turbulent mixing arising from an inclined material interface with realistic surface perturbations and reshocked flow. Phys. Fluids 23 (4), 046101.CrossRefGoogle Scholar
Hejazialhosseini, B., Rossinelli, D. & Koumoutsakos, P. 2013 Vortex dynamics in 3D shock–bubble interaction. Phys. Fluids 25 (11), 110816.CrossRefGoogle Scholar
Houim, R.W. & Kuo, K.K. 2011 A low-dissipation and time-accurate method for compressible multi-component flow with variable specific heat ratios. J. Comput. Phys. 230 (23), 8527–8553.CrossRefGoogle Scholar
Hu, Z.-X., Zhang, Y.-S., Tian, B., He, Z. & Li, L. 2019 Effect of viscosity on two-dimensional single-mode Rayleigh–Taylor instability during and after the reacceleration stage. Phys. Fluids 31 (10), 104108.Google Scholar
Igra, D. & Igra, O. 2020 Shock wave interaction with a polygonal bubble containing two different gases, a numerical investigation. J. Fluid Mech. 889, A26.CrossRefGoogle Scholar
Jacobs, J.W. 1992 Shock-induced mixing of a light-gas cylinder. J. Fluid Mech. 234, 629–649.CrossRefGoogle Scholar
Jiang, G.-S. & Shu, C.-W. 1996 Efficient implementation of weighted ENO schemes. J. Comput. Phys. 126 (1), 202–228.CrossRefGoogle Scholar
Johnsen, E. & Colonius, T. 2006 Implementation of WENO schemes in compressible multicomponent flow problems. J. Comput. Phys. 219 (2), 715–732.CrossRefGoogle Scholar
Kee, R.J., Rupley, F.M., Meeks, E. & Miller, J.A. 1996 CHEMKIN-III: a FORTRAN chemical kinetics package for the analysis of gas-phase chemical and plasma kinetics. Tech. Rep. Sandia National Laboratories.CrossRefGoogle Scholar
Kumar, S., Orlicz, G., Tomkins, C., Goodenough, C., Prestridge, K., Vorobieff, P. & Benjamin, R. 2005 Stretching of material lines in shock-accelerated gaseous flows. Phys. Fluids 17 (8), 082107.CrossRefGoogle Scholar
Layes, G., Jourdan, G. & Houas, L. 2003 Distortion of a spherical gaseous interface accelerated by a plane shock wave. Phys. Rev. Lett. 91 (17), 174502.CrossRefGoogle ScholarPubMed
Lee, S.-H., Jeung, I.-S. & Yoon, Y. 1997 Computational investigation of shock-enhanced mixing and combustion. AIAA J. 35 (12), 1813–1820.CrossRefGoogle Scholar
Li, D., Wang, G. & Guan, B. 2019 On the circulation prediction of shock-accelerated elliptical heavy gas cylinders. Phys. Fluids 31 (5), 056104.CrossRefGoogle Scholar
Li, Y., Wang, Z., Yu, B., Zhang, B. & Liu, H. 2020 Gaussian models for late-time evolution of two-dimensional shock–light cylindrical bubble interaction. Shock Waves 30 (2), 169–184.CrossRefGoogle Scholar
Lin, H., Xiang, Y., Xu, H., Liu, H. & Zhang, B. 2020 Passive scalar mixing induced by the formation of compressible vortex rings. Acta Mechanica Sin. 36 (6), 1258–1274.CrossRefGoogle Scholar
Liu, C.-C., Wang, Z., Yu, B., Zhang, B., Liu, H. 2020 a Optimal excitation mechanism for combustion enhancement of supersonic shear layers with pulsed jets. Intl J. Hydrog. Energy 45 (43), 23674–23691.CrossRefGoogle Scholar
Liu, H.-C., Yu, B., Chen, H., Zhang, B., Xu, H. & Liu, H. 2020 b Contribution of viscosity to the circulation deposition in the Richtmyer–Meshkov instability. J. Fluid Mech. 895, A10.CrossRefGoogle Scholar
Liu, X.-D., Osher, S. & Chan, T. 1994 Weighted essentially non-oscillatory schemes. J. Comput. Phys. 115 (1), 200–212.CrossRefGoogle Scholar
Lombardini, M., Pullin, D.I. & Meiron, D.I. 2012 Transition to turbulence in shock-driven mixing: a Mach number study. J. Fluid Mech. 690, 203–226.CrossRefGoogle Scholar
Luo, X., Wang, M., Si, T. & Zhai, Z. 2015 On the interaction of a planar shock with an SF$_6$ polygon. J. Fluid Mech. 773, 366–394.CrossRefGoogle Scholar
Marble, F.E. 1985 Growth of a diffusion flame in the field of a vortex. In Recent Advances in the Aerospace Sciences, pp. 395–413. Springer.CrossRefGoogle Scholar
Marble, F.E., Hendricks, G.J. & Zukoski, E.E. 1989 Progress Toward Shock Enhancement of Supersonic Combustion Processes. Springer US.CrossRefGoogle Scholar
Marble, F.E., Zukoski, E.E., Jacobs, J., Hendricks, G. & Waitz, I. 1990 Shock enhancement and control of hypersonic mixing and combustion. In 26th Joint Propulsion Conference, p. 1981. AIAA.CrossRefGoogle Scholar
Meunier, P. & Villermaux, E. 2003 How vortices mix. J. Fluid Mech. 476, 213–222.CrossRefGoogle Scholar
Moore, D.W. & Pullin, D.I. 1987 The compressible vortex pair. J. Fluid Mech. 185, 171–204.CrossRefGoogle Scholar
Mosedale, A. & Drikakis, D. 2007 Assessment of very high order of accuracy in implicit LES models. ASME J. Fluids Engng 129 (12), 1497–1503.CrossRefGoogle Scholar
Niederhaus, J.H.J., Greenough, J.A., Oakley, J.G., Ranjan, D., Anderson, M.H. & Bonazza, R. 2008 A computational parameter study for the three-dimensional shock–bubble interaction. J. Fluid Mech. 594, 85–124.CrossRefGoogle Scholar
Oggian, T., Drikakis, D., Youngs, D.L. & Williams, R.J.R. 2015 Computing multi-mode shock-induced compressible turbulent mixing at late times. J. Fluid Mech. 779, 411–431.CrossRefGoogle Scholar
Peng, G., Zabusky, N.J. & Zhang, S. 2003 Vortex-accelerated secondary baroclinic vorticity deposition and late-intermediate time dynamics of a two-dimensional Richtmyer–Meshkov interface. Phys. Fluids 15 (12), 3730–3744.CrossRefGoogle Scholar
Peng, N., Yang, Y., Wu, J. & Xiao, Z. 2021 a Mechanism and modelling of the secondary baroclinic vorticity in the Richtmyer–Meshkov instability. J. Fluid Mech. 911, A56.CrossRefGoogle Scholar
Peng, N., Yang, Y. & Xiao, Z. 2021 b Effects of the secondary baroclinic vorticity on the energy cascade in the Richtmyer–Meshkov instability. J. Fluid Mech. 925, A39.CrossRefGoogle Scholar
Picone, J.M. & Boris, J.P. 1988 Vorticity generation by shock propagation through bubbles in a gas. J. Fluid Mech. 189, 23–51.CrossRefGoogle Scholar
Qin, L., Xiang, Y., Lin, H. & Liu, H. 2020 Formation and dynamics of compressible vortex rings generated by a shock tube. Exp. Fluids 61 (3), 86.CrossRefGoogle Scholar
Quirk, J.J. & Karni, S. 1996 On the dynamics of a shock–bubble interaction. J. Fluid Mech. 318, 129–163.CrossRefGoogle Scholar
Rahmani, M., Lawrence, G.A. & Seymour, B.R. 2014 The effect of Reynolds number on mixing in Kelvin–Helmholtz billows. J. Fluid Mech. 759, 612–641.CrossRefGoogle Scholar
Ranjan, D., Anderson, M., Oakley, J. & Bonazza, R. 2005 Experimental investigation of a strongly shocked gas bubble. Phys. Rev. Lett. 94 (18), 184507.CrossRefGoogle ScholarPubMed
Ranjan, D., Niederhaus, J., Motl, B., Anderson, M., Oakley, J. & Bonazza, R. 2007 Experimental investigation of primary and secondary features in high–Mach–number shock-bubble interaction. Phys. Rev. Lett. 98 (2), 024502.CrossRefGoogle ScholarPubMed
Ranjan, D., Niederhaus, J.H.J., Oakley, J.G., Anderson, M.H., Bonazza, R. & Greenough, J.A. 2008 Shock-bubble interactions: features of divergent shock-refraction geometry observed in experiments and simulations. Phys. Fluids 20 (3), 036101.CrossRefGoogle Scholar
Ranjan, D., Oakley, J. & Bonazza, R. 2011 Shock-bubble interactions. Annu. Rev. Fluid Mech. 43, 117–140.CrossRefGoogle Scholar
Ranz, W.E. 1979 Applications of a stretch model to mixing, diffusion, and reaction in laminar and turbulent flows. AIChE J. 25 (1), 41–47.CrossRefGoogle Scholar
Reinaud, J., Joly, L. & Chassaing, P. 2000 The baroclinic secondary instability of the two-dimensional shear layer. Phys. Fluids 12 (10), 2489–2505.CrossRefGoogle Scholar
Richtmyer, R.D. 1960 Taylor instability in shock acceleration of compressible fluids. Commun. Pure Appl. Math. 13 (2), 297–319.CrossRefGoogle Scholar
Samtaney, R. & Zabusky, N.J. 1994 Circulation deposition on shock-accelerated planar and curved density-stratified interfaces: models and scaling laws. J. Fluid Mech. 269, 45–78.CrossRefGoogle Scholar
Sau, R. & Mahesh, K. 2007 Passive scalar mixing in vortex rings. J. Fluid Mech. 582, 449–461.CrossRefGoogle Scholar
Schetz, J.A., Maddalena, L. & Burger, S.K. 2010 Molecular weight and shock-wave effects on transverse injection in supersonic flow. J. Propul. Power 26 (5), 1102–1113.CrossRefGoogle Scholar
Shankar, S.K., Kawai, S. & Lele, S.K. 2011 Two-dimensional viscous flow simulation of a shock accelerated heavy gas cylinder. Phys. Fluids 23 (2), 024102.CrossRefGoogle Scholar
Shariff, K. & Leonard, A. 1992 Vortex rings. Annu. Rev. Fluid Mech. 24 (1), 235–279.CrossRefGoogle Scholar
Si, T., Long, T., Zhai, Z. & Luo, X. 2015 Experimental investigation of cylindrical converging shock waves interacting with a polygonal heavy gas cylinder. J. Fluid Mech. 784, 225–251.CrossRefGoogle Scholar
Socolofsky, S.A. & Jirka, G.H. 2005 Special topics in mixing and transport processes in the environment. In Engineering–Lectures, 5th edn, pp. 1–93. Texas A&M University.Google Scholar
Tew, D.E., Hermanson, J.C. & Waitz, I.A. 2004 Impact of compressibility on mixing downstream of lobed mixers. AIAA J. 42 (11), 2393–2396.CrossRefGoogle Scholar
Thornber, B., Drikakis, D., Youngs, D.L. & Williams, R.J.R. 2010 The influence of initial conditions on turbulent mixing due to Richtmyer–Meshkov instability. J. Fluid Mech. 654, 99–139.CrossRefGoogle Scholar
Thornber, B., Drikakis, D., Youngs, D.L. & Williams, R.J.R. 2011 Growth of a Richtmyer–Meshkov turbulent layer after reshock. Phys. Fluids 23 (9), 095107.CrossRefGoogle Scholar
Tomkins, C., Kumar, S., Orlicz, G. & Prestridge, K. 2008 An experimental investigation of mixing mechanisms in shock-accelerated flow. J. Fluid Mech. 611, 131–150.CrossRefGoogle Scholar
Tritschler, V.K., Hu, X.Y., Hickel, S. & Adams, N.A. 2013 Numerical simulation of a Richtmyer–Meshkov instability with an adaptive central-upwind sixth-order WENO scheme. Phys. Scripta 2013 (T155), 014016.CrossRefGoogle Scholar
Tritschler, V.K., Olson, B.J., Lele, S.K., Hickel, S., Hu, X.Y. & Adams, N.A. 2014 On the Richtmyer–Meshkov instability evolving from a deterministic multimode planar interface. J. Fluid Mech. 755, 429–462.CrossRefGoogle Scholar
Urzay, J. 2018 Supersonic combustion in air-breathing propulsion systems for hypersonic flight. Annu. Rev. Fluid Mech. 50, 593–627.CrossRefGoogle Scholar
Vergine, F., Ground, C. & Maddalena, L. 2016 Turbulent kinetic energy decay in supersonic streamwise interacting vortices. J. Fluid Mech. 807, 353–385.CrossRefGoogle Scholar
Villermaux, E. 2019 Mixing versus stirring. Annu. Rev. Fluid Mech. 51, 245–273.CrossRefGoogle Scholar
Vorobieff, P., Rightley, P.M. & Benjamin, R.F. 1998 Power-law spectra of incipient gas-curtain turbulence. Phys. Rev. Lett. 81 (11), 2240.CrossRefGoogle Scholar
Waitz, I.A., Marble, F.E. & Zukoski, E.E. 1993 Investigation of a contoured wall injector for hypervelocity mixing augmentation. AIAA J. 31 (6), 1014–1021.CrossRefGoogle Scholar
Waitz, I.A., et al. 1997 Enhanced mixing with streamwise vorticity. Prog. Aerosp. Sci. 33 (5–6), 323–351.CrossRefGoogle Scholar
Walchli, B. & Thornber, B. 2017 Reynolds number effects on the single-mode Richtmyer–Meshkov instability. Phys. Rev. E 95 (1), 013104.CrossRefGoogle ScholarPubMed
Wang, Z., Yu, B., Chen, H., Zhang, B. & Liu, H. 2018 Scaling vortex breakdown mechanism based on viscous effect in shock cylindrical bubble interaction. Phys. Fluids 30 (12), 126103.CrossRefGoogle Scholar
Wang, Z., Yu, B., Zhang, B., He, M. & Liu, H. 2021 Kinematic and mixing characteristics of vortex interaction induced by a vortex generator model: a numerical study. Appl. Math. Mech. 42 (3), 387–404.CrossRefGoogle Scholar
Wasik, S.P. & McCulloh, K.E. 1969 Measurements of gaseous diffusion coefficients by a gas chromatographic technique. J. Res. Natl Bur. Stand. A Phys. Chem. 73 (2), 207.CrossRefGoogle Scholar
Weber, C., Haehn, N., Oakley, J., Rothamer, D. & Bonazza, R. 2012 Turbulent mixing measurements in the Richtmyer–Meshkov instability. Phys. Fluids 24 (7), 074105.CrossRefGoogle Scholar
Weber, C.R., Haehn, N.S., Oakley, J.G., Rothamer, D.A. & Bonazza, R. 2014 An experimental investigation of the turbulent mixing transition in the Richtmyer–Meshkov instability. J. Fluid Mech. 748, 457–487.CrossRefGoogle Scholar
Wu, J.-Z., Ma, H.-Y. & Zhou, M.-D. 2007 Vorticity and Vortex Dynamics. Springer Science & Business Media.Google Scholar
Yang, J., Kubota, T. & Zukoski, E.E. 1993 Applications of shock-induced mixing to supersonic combustion. AIAA J. 31 (5), 854–862.CrossRefGoogle Scholar
Yang, J., Kubota, T. & Zukoski, E.E. 1994 A model for characterization of a vortex pair formed by shock passage over a light-gas inhomogeneity. J. Fluid Mech. 258, 217–244.CrossRefGoogle Scholar
Yu, B., He, M., Zhang, B. & Liu, H. 2020 Two-stage growth mode for lift-off mechanism in oblique shock-wave/jet interaction. Phys. Fluids 32 (11), 116105.CrossRefGoogle Scholar
Yu, B., Liu, H. & Liu, H. 2021 Scaling behavior of density gradient accelerated mixing rate in shock bubble interaction. Phys. Rev. Fluids 6 (6), 064502.CrossRefGoogle Scholar
Zabusky, N.J. 1999 Vortex paradigm for accelerated inhomogeneous flows: visiometrics for the Rayleigh–Taylor and Richtmyer–Meshkov environments. Annu. Rev. Fluid Mech. 31 (1), 495–536.CrossRefGoogle Scholar
Zhai, Z., Si, T., Luo, X. & Yang, J. 2011 On the evolution of spherical gas interfaces accelerated by a planar shock wave. Phys. Fluids 23 (8), 084104.CrossRefGoogle Scholar
Zhang, B., Liu, H., Yu, B., Wang, Z., He, M. & Liu, H. 2021 Numerical investigation on combustion-enhancement strategy in shock–fuel jet interaction. AIAA J. https://doi.org/10.2514/1.J060168.CrossRefGoogle Scholar
Zhang, Y.-T., Shi, J., Shu, C.-W. & Zhou, Y. 2003 Numerical viscosity and resolution of high-order weighted essentially nonoscillatory schemes for compressible flows with high Reynolds numbers. Phys. Rev. E 68 (4), 046709.CrossRefGoogle ScholarPubMed
Zhou, Y., et al. 2021 Rayleigh–Taylor and Richtmyer–Meshkov instabilities: a journey through scales. Physica D, 132838.CrossRefGoogle Scholar