Article contents
Collapse of transitional wall turbulence captured using a rare events algorithm
Published online by Cambridge University Press: 26 November 2021
Abstract
This text presents one of the first successful applications of a rare events sampling method for the study of multistability in a turbulent flow without stochastic energy injection. The trajectories of collapse of turbulence in plane Couette flow, and their probability and rate of occurrence are systematically computed using adaptive multilevel splitting (AMS). The AMS computations are performed in a system of size  $L_x\times L_z=24\times 18$ at Reynolds number
$L_x\times L_z=24\times 18$ at Reynolds number  $R=370$ with an acceleration by a factor
$R=370$ with an acceleration by a factor  ${O}(10)$ with respect to direct numerical simulations (DNS) and in a system of size
${O}(10)$ with respect to direct numerical simulations (DNS) and in a system of size  $L_x\times L_z=36\times 27$ at Reynolds number
$L_x\times L_z=36\times 27$ at Reynolds number  $R=377$ with an acceleration by a factor
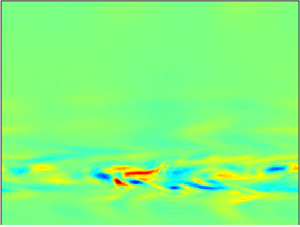
$R=377$ with an acceleration by a factor  ${O}(10^3)$. The AMS results are validated by a comparison with DNS in the smaller system. Visualisations indicate that turbulence collapses because the self-sustaining process of turbulence fails locally. The streamwise vortices decay first in streamwise elongated holes, leaving streamwise invariant streamwise velocity tubes that experience viscous decay. These holes then extend in the spanwise direction. The examination of more than a thousand trajectories in the
${O}(10^3)$. The AMS results are validated by a comparison with DNS in the smaller system. Visualisations indicate that turbulence collapses because the self-sustaining process of turbulence fails locally. The streamwise vortices decay first in streamwise elongated holes, leaving streamwise invariant streamwise velocity tubes that experience viscous decay. These holes then extend in the spanwise direction. The examination of more than a thousand trajectories in the  $(E_{k,x}=\int u_x^2/2\,\textrm {d}^3\boldsymbol {x},E_{k,y-z}=\int (u_y^2/2+u_z^2/2)\,\textrm {d}^3\boldsymbol {x})$ plane in the smaller system confirms the faster decay of streamwise vortices and shows concentration of trajectories. This hints at an instanton phenomenology in the large size limit. The computation of turning point states, beyond which laminarisation is certain, confirms the hole formation scenario and shows that it is more pronounced in larger systems. Finally, the examination of non-reactive trajectories indicates that both the vortices and the streaks reform concomitantly when the laminar holes close.
$(E_{k,x}=\int u_x^2/2\,\textrm {d}^3\boldsymbol {x},E_{k,y-z}=\int (u_y^2/2+u_z^2/2)\,\textrm {d}^3\boldsymbol {x})$ plane in the smaller system confirms the faster decay of streamwise vortices and shows concentration of trajectories. This hints at an instanton phenomenology in the large size limit. The computation of turning point states, beyond which laminarisation is certain, confirms the hole formation scenario and shows that it is more pronounced in larger systems. Finally, the examination of non-reactive trajectories indicates that both the vortices and the streaks reform concomitantly when the laminar holes close.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 9
- Cited by



