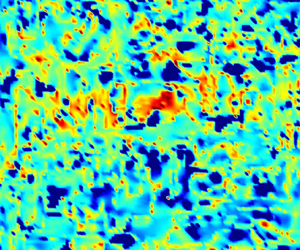
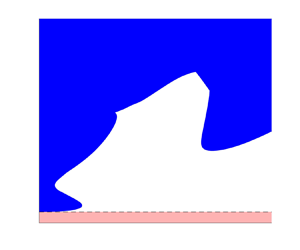
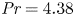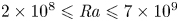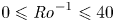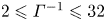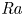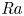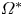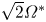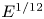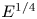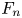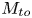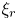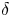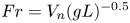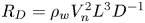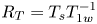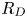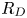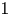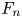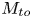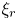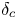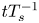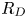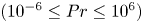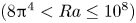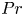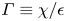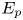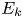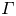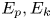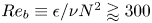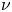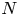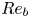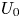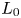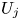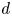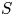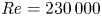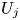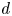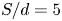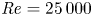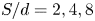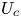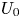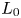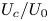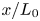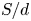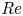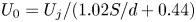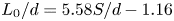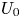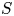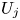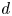Graphical abstract from Di Vaira, N., Łaniewski-Wołłk, Ł., Johnson, R., Aminossadati, S. & Leonardi, C. 2022 Influence of particle polydispersity on bulk migration and size segregation in channel flows. J. Fluid Mech. 939, A30. doi:10.1017/jfm.2022.166.
JFM Rapids
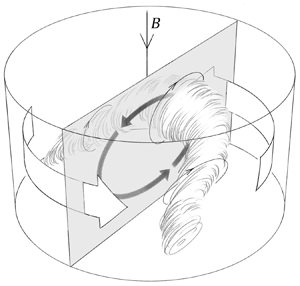
Experimental pub crawl from Rayleigh–Bénard to magnetostrophic convection
-
- Published online by Cambridge University Press:
- 23 March 2022, R1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bistability of the large-scale dynamics in quasi-two-dimensional turbulence
-
- Published online by Cambridge University Press:
- 24 March 2022, R2
-
- Article
- Export citation
JFM Papers
Multiple heat transport maxima in confined-rotating Rayleigh–Bénard convection
-
- Published online by Cambridge University Press:
- 24 March 2022, A1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Accurate prediction of the particle image velocimetry flow field and rotor thrust using deep learning
-
- Published online by Cambridge University Press:
- 23 March 2022, A2
-
- Article
- Export citation
Internal shear layers in librating spherical shells: the case of periodic characteristic paths
-
- Published online by Cambridge University Press:
- 23 March 2022, A3
-
- Article
- Export citation
The controlled impact of elastic plates on a quiescent water surface
-
- Published online by Cambridge University Press:
- 23 March 2022, A4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A data-driven model based on modal decomposition: application to the turbulent channel flow over an anisotropic porous wall
-
- Published online by Cambridge University Press:
- 23 March 2022, A5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The spatial structure of electrostatically forced Faraday waves
-
- Published online by Cambridge University Press:
- 23 March 2022, A6
-
- Article
- Export citation
On transport tensor of dynamically unresolved oceanic mesoscale eddies
-
- Published online by Cambridge University Press:
- 23 March 2022, A7
-
- Article
- Export citation
The onset of zonal modes in two-dimensional Rayleigh–Bénard convection
-
- Published online by Cambridge University Press:
- 23 March 2022, A8
-
- Article
- Export citation
Molecular kinetic modelling of nanoscale slip flow using a continuum approach
-
- Published online by Cambridge University Press:
- 23 March 2022, A9
-
- Article
- Export citation
Implications of inertial subrange scaling for stably stratified mixing
-
- Published online by Cambridge University Press:
- 24 March 2022, A10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A sparse optimal closure for a reduced-order model of wall-bounded turbulence
-
- Published online by Cambridge University Press:
- 24 March 2022, A11
-
- Article
- Export citation
Thermal fluctuations in the dissipation range of homogeneous isotropic turbulence
-
- Published online by Cambridge University Press:
- 24 March 2022, A12
-
- Article
- Export citation
Development and scaling of turbulent, twin round jets
-
- Published online by Cambridge University Press:
- 29 March 2022, A13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Experimental evidence for the boundary zonal flow in rotating Rayleigh–Bénard convection
-
- Published online by Cambridge University Press:
- 24 March 2022, A14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Reflectionless wave propagation on shallow water with variable bathymetry and current. Part 2
-
- Published online by Cambridge University Press:
- 24 March 2022, A15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On shock-induced evolution of a gas layer with two fast/slow interfaces
-
- Published online by Cambridge University Press:
- 24 March 2022, A16
-
- Article
- Export citation
Exponential asymptotics for steady parasitic capillary ripples on steep gravity waves
-
- Published online by Cambridge University Press:
- 30 March 2022, A17
-
- Article
- Export citation
Immersed body motion: near-bottom added mass effects
-
- Published online by Cambridge University Press:
- 30 March 2022, A18
-
- Article
- Export citation