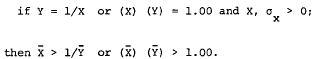Research Article
A Note on Indifference Curves in the Mean-Variance Model
-
- Published online by Cambridge University Press:
- 19 October 2009, pp. 121-126
-
- Article
- Export citation
Simple Goodness-of-Fit Tests for Symmetric Stable Distributions
-
- Published online by Cambridge University Press:
- 19 October 2009, pp. 276-289
-
- Article
- Export citation
Forward Exchange Price Determination in Continuous Time
-
- Published online by Cambridge University Press:
- 19 October 2009, pp. 473-479
-
- Article
- Export citation
Proceedings of 1977 Western Finance Association Meeting: Selected Conference Papers
Teaching International Finance–An Accountant's Perspective
-
- Published online by Cambridge University Press:
- 19 October 2009, pp. 609-614
-
- Article
- Export citation
Research Article
Multiperiod Capital Budgeting under Uncertainty: A Suggested Application
-
- Published online by Cambridge University Press:
- 19 October 2009, pp. 859-877
-
- Article
- Export citation
Comment: “An Autoregressive Forecast of the World Sugar Future Option Market”
-
- Published online by Cambridge University Press:
- 19 October 2009, pp. 879-881
-
- Article
- Export citation
Bond Portfolio Strategies, Returns, and Skewness: A Note
-
- Published online by Cambridge University Press:
- 19 October 2009, pp. 127-140
-
- Article
- Export citation
Proceedings of 1977 Western Finance Association Meeting: Selected Conference Papers
The Relationship between Risk of Default and Return on Equity: An Empirical Investigation
-
- Published online by Cambridge University Press:
- 19 October 2009, pp. 615-625
-
- Article
- Export citation
Research Article
An Analytical Model of Interest Rate Differentials and Different Default Recoveries
-
- Published online by Cambridge University Press:
- 19 October 2009, pp. 481-490
-
- Article
- Export citation
Evidence on the Presence and Causes of Serial Correlation in Market Model Residuals
-
- Published online by Cambridge University Press:
- 19 October 2009, pp. 291-313
-
- Article
- Export citation
A Warning Note on Empirical Research Using Foreign Exchange Rates
-
- Published online by Cambridge University Press:
- 19 October 2009, pp. 315-319
-
- Article
- Export citation
A Ranking of Doctoral Programs by Financial Research Contributions of Graduates
-
- Published online by Cambridge University Press:
- 19 October 2009, pp. 491-497
-
- Article
- Export citation
Abstracts of Conference Papers: Capital Market Theory
Abstract: An Equilibrium Characterization of the Term Structure
-
- Published online by Cambridge University Press:
- 19 October 2009, p. 627
-
- Article
- Export citation
Research Article
Comment: “An Autoregressive Forecast of the World Sugar Future Option Market”
-
- Published online by Cambridge University Press:
- 19 October 2009, pp. 883-890
-
- Article
- Export citation
Security Price Changes and Transaction Volumes: Some Additional Evidence
-
- Published online by Cambridge University Press:
- 19 October 2009, pp. 141-146
-
- Article
- Export citation
Utility Analysis of Chance-Constrained Portfolio Selection: A Correction
-
- Published online by Cambridge University Press:
- 19 October 2009, pp. 321-323
-
- Article
- Export citation
A Reformulation of the API Approach to Evaluating Accounting Income Numbers
-
- Published online by Cambridge University Press:
- 19 October 2009, pp. 499-504
-
- Article
- Export citation
Comment: “An Investment Paradox”
-
- Published online by Cambridge University Press:
- 19 October 2009, pp. 891-894
-
- Article
- Export citation
Announcement
Announcements
-
- Published online by Cambridge University Press:
- 19 October 2009, pp. 147-149
-
- Article
-
- You have access
- Export citation
Abstracts of Conference Papers: International Finance
Abstract: Characterizations of Exchange Convertibility Schemes: A Structure for Analysis
-
- Published online by Cambridge University Press:
- 19 October 2009, p. 629
-
- Article
- Export citation