Article contents
Utility Analysis of Chance-Constrained Portfolio Selection: A Correction
Published online by Cambridge University Press: 19 October 2009
Extract
In [1, p. 999] I wrongly stated that “the solution locus generated by the chance-constrained problem is efficient (for the class of utility function implied by the expected wealth-probability of ruin criterion) if the assets follow a multinomial distribution with means above the survival level.” In support of this statement footnote 6 of [1] attempted to establish the quasiconcavity of the expected utility function

in the (μ, σ) plane, where F is the normal distribution, z = (s-μ)/σ < 0, s is the survival level, μ is the mean of the portfolio, σ is the standard deviation, and c is a positive constant. The condition
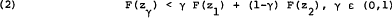
was claimed to hold for any two assets (μ1., σ1) and (μ2., σ2) on any given indifference curve of (1), where zi. = (s-μi.)/σi., i = 1,2, and zγ = (s−μγ)/σγ corresponds to the convex combination μγ = γμ1 + (1−γ) μ2, σγ = γσ1+ (1−γ) σ2, in the (μ, σ) plane. (Note that this is not the same as asserting that F(z) is a convex function of μ and σ, which it is not as an examination of its Hessian determinant would readily show.)
- Type
- Research Article
- Information
- Copyright
- Copyright © School of Business Administration, University of Washington 1977
References
REFERENCE
- 1
- Cited by


