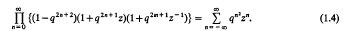Research Article
Matrix representations of semigroups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 1-13
-
- Article
-
- You have access
- Export citation
The distribution of the residues of a quartic polynomial
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 67-88
-
- Article
-
- You have access
- Export citation
Proof of a conjecture of Ramanujan
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 14-32
-
- Article
-
- You have access
- Export citation
On maximal nilpotent subrings of right Noetherian rings
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 89-101
-
- Article
-
- You have access
- Export citation
On Riemann surfaces with maximal automorphism groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 102-112
-
- Article
-
- You have access
- Export citation
Enumerative proofs of certain q-identities
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 33-40
-
- Article
-
- You have access
- Export citation
Hilbert transforms and unitary equivalence
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 113-117
-
- Article
-
- You have access
- Export citation
Compact linear operators from an algebraic standpoint
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 41-49
-
- Article
-
- You have access
- Export citation
Some integral equations involving finite parts of divergent integrals
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 50-54
-
- Article
-
- You have access
- Export citation
On products of idempotent matrices
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 118-122
-
- Article
-
- You have access
- Export citation
Some results on coherent rings II
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 123-126
-
- Article
-
- You have access
- Export citation
Naturally ordered bands
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 55-58
-
- Article
-
- You have access
- Export citation
On Schur's second partition theorem
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 127-132
-
- Article
-
- You have access
- Export citation
A new class of Hadamard matrices
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 59-62
-
- Article
-
- You have access
- Export citation
Automorphisms of the semigroup of all differentiable functions
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 63-66
-
- Article
-
- You have access
- Export citation
On the nonexistence of Lp solutions of certain nonlinear differential equations
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 133-138
-
- Article
-
- You have access
- Export citation
Front matter
GMJ volume 8 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
GMJ volume 8 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f6
-
- Article
-
- You have access
- Export citation
Back matter
GMJ volume 8 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation
GMJ volume 8 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation