Article contents
The distribution of the residues of a quartic polynomial
Published online by Cambridge University Press: 18 May 2009
Extract
Let f(x) denote a polynomial of degree d defined over a finite field k with q = pnelements. B. J. Birch and H. P. F. Swinnerton-Dyer [1] have estimated the number N(f) of distinct values of y in k for which at least one of the roots of

is in k. They prove, using A. Weil's deep results [12] (that is, results depending on the Riemann hypothesis for algebraic function fields over a finite field) on the number of points on a finite number of curves, that

where λ is a certain constant and the constant implied by the O-symbol depends only on d. In fact, if G(f) denotes the Galois group of the equation (1.1) over k(y) and G+(f) its Galois group over k+(y), where k+ is the algebraic closure of k, then it is shown that λ depends only on G(f), G+(f) and d. It is pointed out that “in general”
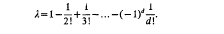
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1967
- 8
- Cited by


