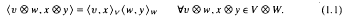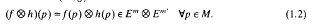Research Article
Barrelled subspaces of spaces with subseries decompositions or Boolean rings of projections
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 57-69
-
- Article
-
- You have access
- Export citation
The Chen-type of the noncompact cyclides of Dupin
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 71-75
-
- Article
-
- You have access
- Export citation
On quasi-permutation representations of finite groups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 301-308
-
- Article
-
- You have access
- Export citation
Linearization of holomorphic mappings on fully nuclear spaces with a basis
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 201-208
-
- Article
-
- You have access
- Export citation
Some results on stable p-harmonic maps
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 77-80
-
- Article
-
- You have access
- Export citation
The structure of discontinuous homomorphisms from non-commutative C*-algebras
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 209-218
-
- Article
-
- You have access
- Export citation
On dilation equations and the Hölder continuity of the de Rham functions
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 309-311
-
- Article
-
- You have access
- Export citation
The kernel and trace operators for ideal extensions of regular semigroups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 219-231
-
- Article
-
- You have access
- Export citation
On an arithemtical inequality
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 81-86
-
- Article
-
- You have access
- Export citation
Automorphism groups of complex doubles of Klein surfaces
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 313-330
-
- Article
-
- You have access
- Export citation
Local spectral theory and spectral inclusions
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 331-343
-
- Article
-
- You have access
- Export citation
Finite metacyclic groups acting on bordered surfaces
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 233-240
-
- Article
-
- You have access
- Export citation
Minimal Cockcroft subgroups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 87-90
-
- Article
-
- You have access
- Export citation
Pure-semisimplicity is preserved under elementary equivalence
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 345-346
-
- Article
-
- You have access
- Export citation
Conjugacy classes in sylow p-subgroups of GL(n, q), IV†
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 91-96
-
- Article
-
- You have access
- Export citation
On 𝓕-subnormal subgroups and Frattini-like subgroups of a finite group
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 241-247
-
- Article
-
- You have access
- Export citation
A weaker condition for normality
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 249-253
-
- Article
-
- You have access
- Export citation
Almost factorisable inverse semigroups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 97-111
-
- Article
-
- You have access
- Export citation
Complete slices and homological properties of tilted algebras
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 347-354
-
- Article
-
- You have access
- Export citation
Classification of tensor product immersions which are of 1-type
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 255-264
-
- Article
-
- You have access
- Export citation

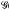 (
(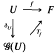

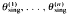 :
: 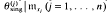
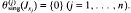 is a homomorphism, and
is a homomorphism, and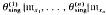
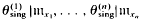 to map into rad(
to map into rad(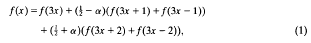

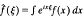 is the Fourier transform of
is the Fourier transform of 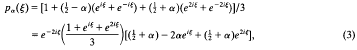



 , the Sylow
, the Sylow 
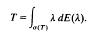
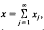 then this sum must converge unconditionally.
then this sum must converge unconditionally.