Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T20:23:01.316Z Has data issue: false hasContentIssue false
  • English
  • Français

Linearization of holomorphic mappings on fully nuclear spaces with a basis

Published online by Cambridge University Press:  18 May 2009

Seán Dineen ,
Pablo Galindo ,
Domingo García  and
Manuel Maestre
Seán Dineen
Affiliation:
Department of Mathematics, University College, Dublin, Dublin 4, Ireland
Pablo Galindo
Affiliation:
Department de Análisis Matemático, Facultad de Matemáticas, Universidad de Valencia, 46100 Burjasot (Valencia), Spain
Domingo García
Affiliation:
Department de Análisis Matemático, Facultad de Matemáticas, Universidad de Valencia, 46100 Burjasot (Valencia), Spain
Manuel Maestre
Affiliation:
Department de Análisis Matemático, Facultad de Matemáticas, Universidad de Valencia, 46100 Burjasot (Valencia), Spain
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [13] Mazet proved the following result.

If U is an open subset of a locally convex space E then there exists a complete locally convex space 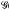(U) and a holomorphic mapping δU: U→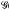(U) such that for any complete locally convex space F and any f ɛ ℋ (U;F), the space of holomorphic mappings from U to F, there exists a unique linear mapping Tf: 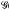(U)→F such that the following diagram commutes;

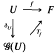
The space 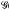(U) is unique up to a linear topological isomorphism. Previously, similar but less general constructions, have been considered by Ryan [16] and Schottenloher [17].

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 36 , Issue 2 , May 1994 , pp. 201 - 208
Copyright
Copyright © Glasgow Mathematical Journal Trust 1994

References

REFERENCES

1.Barroso, J. A., Matos, M. C. and Nachbin, L., On holomorphy versus linearity in classifying locally convex spaces, in Infinite dimensional holomorphy and applications (North Holland Math. Studies) 12 (1977), 31–74.CrossRefGoogle Scholar
2.Berner, P., Topologies on spaces of holomorphic functions on certain surjective limits, in Infinite dimensional holomorphy and applications (North-Holland Math. Studies) 12 (1977), 75–92.CrossRefGoogle Scholar
3.Bierstedt, K. D., An introduction to locally convex inductive limits (World Scientific Publ. Co., Singapore, 1988).Google Scholar
4.Boland, P. J. and Dineen, S., Holomorphic functions on fully nuclear spaces, Bull. Soc. Math. France 103 (1978), 311–335.CrossRefGoogle Scholar
5.Boland, P. J. and Dineen, S., Holomorphy on spaces of distributions. Pacific J. Math., 92 (1981), 27–34.CrossRefGoogle Scholar
6.Bonet, J. and Carreras, P. Perez, Barrelled locally convex spaces (North Holland Math. Studies) 131 (1987)).Google Scholar
7.Bonet, J., Galindo, P., García, D. and Maestre, M., Locally bounded sets of holomorphic mappings, Trans. Amer. Math. Soc., 309 (1988), 609–620.CrossRefGoogle Scholar
8.Dineen, S., Holomorphic functions on locally convex topological vector spaces I; locally convex topologies on ℋ(U), Ann. Inst. Fourier, 23 (1973), 19–54.CrossRefGoogle Scholar
9.Dineen, S., Holomorphic functions on strong duals of Fréchet–Montel spaces, in Infinite dimensional holomorphy and applications (North Holland Math. Studies) 12 (1977), 147–166.CrossRefGoogle Scholar
10.Dineen, S., Complex analysis in locally convex spaces (North-Holland Math. Studies) 57 (1981).CrossRefGoogle Scholar
11.Dineen, S., Analytic functionals on fully nuclear spaces, Studia Math. 73 (1982), 11–32.CrossRefGoogle Scholar
12.Horvath, J., Topological vector spaces and distributions I (Addison-Wesley, 1966).Google Scholar
13.Mazet, P., Analytic sets in locally convex spaces (North Holland Math. Studies) 89 (1984).Google Scholar
14.Moraes, L. A., Holomorphic functions on strict inductive limits, Resultate der Math. 4 (1981), 201–212.CrossRefGoogle Scholar
15.Mujica, J. and Nachbin, L., Linearization of holomorphic mappings on locally convex spaces J. Math. Pures Appl. 71 (1992), 543–560.Google Scholar
16.Ryan, R. A., Applications of topological tensor products to infinite dimensional holomorphy, Ph.D. thesis, Trinity College, Dublin (1980).Google Scholar
17.Schottenloher, M., ɛ-products and continuation of analytic mappings, in Analyse Fonction nelle et Applications (Hermann, Paris, 1975), 261–270.Google Scholar