Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-23T22:09:50.816Z Has data issue: false hasContentIssue false
  • English
  • Français

Conjugacy classes in sylow p-subgroups of GL(n, q), IV†

Published online by Cambridge University Press:  18 May 2009

A. Vera-López  and
J. M. Arregi
A. Vera-López
Affiliation:
Departamento de Matemáticas, Universidad del País Vasco, Apartado 644, Bilbao, Spain
J. M. Arregi
Affiliation:
Departamento de Matemáticas, Universidad del País Vasco, Apartado 644, Bilbao, Spain
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

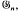In this paper we give new information about the conjugacy vector of the group , the Sylow p-subgroup of GL(n, q) consisting of the upper unitriangular matrices. The first two components of this vector are given in [4]. Here, we obtain the third component, that is, the number of conjugacy classes whose centralizer has qn+l elements. Besides, we give the whole set of numbers which compose this vector:

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 36 , Issue 1 , January 1994 , pp. 91 - 96
Copyright
Copyright © Glasgow Mathematical Journal Trust 1994

References

REFERENCES

1.Higman, G., Enumerating p-groups. I: Inequalities. Proc. London Math. Soc. (3) 10 (1960), 24–30.CrossRefGoogle Scholar
2.Vera-López, A. and Arregi, J. M., Classes de conjugaison dans les p-sous-groupes de Sylow de GL(n, q). C. R. Acad. Sci. Ser. I. Math. 310 (1990), 81–84.Google Scholar
3.Vera-López, A. and Arregi, J. M., Conjugacy classes in Sylow p-subgroups of GL(n, q). J. Algebra 152, No. 1 (1992), 1–19.CrossRefGoogle Scholar
4.Vera-López, A. and Arregi, J. M., Conjugacy classes in Sylow p-subgroups of GL(n, q), II. Proc. Roy. Soc. Edinburgh, 119A (1991), 343–346.CrossRefGoogle Scholar
5.Vera-López, A. and Arregi, J. M., Classes de conjugaison dans les p-sous-groupes de Sylow de GL(n, q), III. (to appear).Google Scholar