Research Article
Asymptotic formulae for linear oscillations
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 105-111
-
- Article
-
- You have access
- Export citation
Infinite integrals involving products of Legendre functions
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 111-118
-
- Article
-
- You have access
- Export citation
Certain expansions involving E-functions
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 119-122
-
- Article
-
- You have access
- Export citation
On strong Rieszian summability
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 123-131
-
- Article
-
- You have access
- Export citation
A note on Mathieu functions
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 132-134
-
- Article
-
- You have access
- Export citation
Completely continuous movements in topological vector spaces
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 135-141
-
- Article
-
- You have access
- Export citation
On certain relations between products of bilateral hypergeometric series
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 141-144
-
- Article
-
- You have access
- Export citation
Semigroups satisfying minimal conditions
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 145-152
-
- Article
-
- You have access
- Export citation
Front matter
GMJ volume 3 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
GMJ volume 3 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

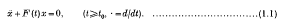
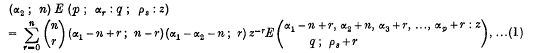
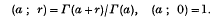

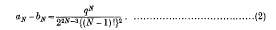
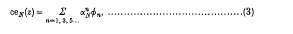
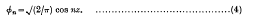
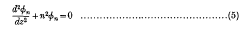

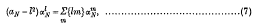
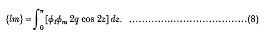
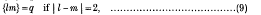
 series in terms of
series in terms of