Hostname: page-component-745bb68f8f-kw2vx Total loading time: 0 Render date: 2025-01-26T14:15:54.223Z Has data issue: false hasContentIssue false
  • English
  • Français

Certain expansions involving E-functions

Published online by Cambridge University Press:  18 May 2009

V. N. Singh
V. N. Singh
Affiliation:
Department of Mathematics and Astronomy, The University Lucknow, India
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The E-functions were defined by MacRobert [3] in 1937; they are denoted by E (p; αr: q; ps. z).

In § 3 of this paper, I prove a new expansion for E(p; αr: q; ps: z) which is similar to an expansion due to MacRobert [2], viz.,

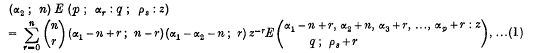
where

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 3 , Issue 3 , December 1957 , pp. 119 - 122
Copyright
Copyright © Glasgow Mathematical Journal Trust 1957

References

REFERENCES

1.Erdélyi, A., Higher transcendental functions (Bateman Manuscript Project), Vol. I (New York, 1953).Google Scholar
2.MacRobert, T. M., On an identity involving E-functions, Phil. Mag. (7), 39 (1948), 466–471.CrossRefGoogle Scholar
3.MacRobert, T. M., Induction proofs of the relations between certain asymptotic expansions and the corresponding generalized hypergeometric functions, Proc. Roy. Soc. Edinburgh, 58 (1937), 1–13.Google Scholar