A note on Mathieu functions

Extract

The Mathieu functions of integral order [1] are the solutions with period π or 2π of the equation

The eigenvalues associated with the functions ce_N and se_N, where N is a positive integer, denoted by a_N and b_N respectively, reduce to

a^N = b_N = N²

when q is zero. The quantities a_N and b_N can be expanded in powers of q, but the explicit construction of high order coefficients is very tedious. In some applications the quantity of most interest is a_N – b_N, which may be called the “width of the unstable zone“. It is the object of this note to derive a general formula for the leading term in the expansion of this quantity, namely

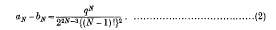
Suppose first that N is an odd integer. Then there is an expansion

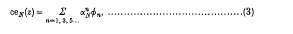
where

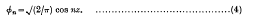
These functions π satisfy

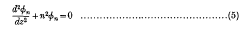
and

On Substituting (3) in (1), one obtains the algebraic equation

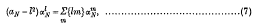
where

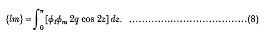
Explicitly,

{11} = q

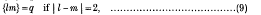
{lm} = 0 otherwise.