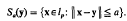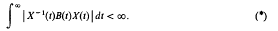Research Article
The a-points of Faber polynomials for a special function†
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 1-6
-
- Article
-
- You have access
- Export citation
Hereditary semisimple classes
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 7-8
-
- Article
-
- You have access
- Export citation
The solution of some integral equations and their connection with dual integral equations and series
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 9-20
-
- Article
-
- You have access
- Export citation
Some arithmetical functions in finite fields
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 21-36
-
- Article
-
- You have access
- Export citation
On bornological products
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 37-40
-
- Article
-
- You have access
- Export citation
Über Automorphiefaktoren und die Dedekindschen Summen
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 41-57
-
- Article
-
- You have access
- Export citation
Homomorphic images of restrictive star semigroups
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 58-71
-
- Article
-
- You have access
- Export citation
Packing of spheres in lp†
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 72-80
-
- Article
-
- You have access
- Export citation
A necessary and sufficient condition for simultaneous diagonalization of two hermitian matrices and its application
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. 81-83
-
- Article
-
- You have access
- Export citation
Corrigenda
Remarks on the Asymptotic Behaviour of Perturbed Linear Systems†
-
- Published online by Cambridge University Press:
- 18 May 2009, p. 84
-
- Article
-
- You have access
- Export citation
Front matter
GMJ volume 11 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back-matter
GMJ volume 11 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 18 May 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation


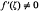 at ζ = ∞ the analytic element is univalent in some neighborhood of infinity; thus the inverse of this element is uniquely determined in some neighborhood of
at ζ = ∞ the analytic element is univalent in some neighborhood of infinity; thus the inverse of this element is uniquely determined in some neighborhood of 
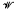 if and only if it has the following properties:
if and only if it has the following properties: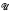 , where
, where 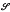 ℘ is hereditary for a radical class ℘ if and only if ℘(
℘ is hereditary for a radical class ℘ if and only if ℘(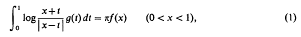
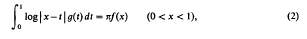
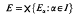
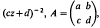 , hat man einen Zweig
, hat man einen Zweig 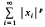 is convergent, with the norm defined by
is convergent, with the norm defined by